формула через диаметр и высоту
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение объема цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
- Формула вычисления объема цилиндра
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту
- Примеры задач
Формула вычисления объема цилиндра
Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H
Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R2. Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2)2 ⋅ H
Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см2, а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)2 ⋅ 6 см = 301,44 см3.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
| Радиус: | ||
| Высота: | ||
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Формула объема цилиндра: , где R – радиус оснований, h – высота цилиндра | ||
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м3 умножить на 1000.
Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах.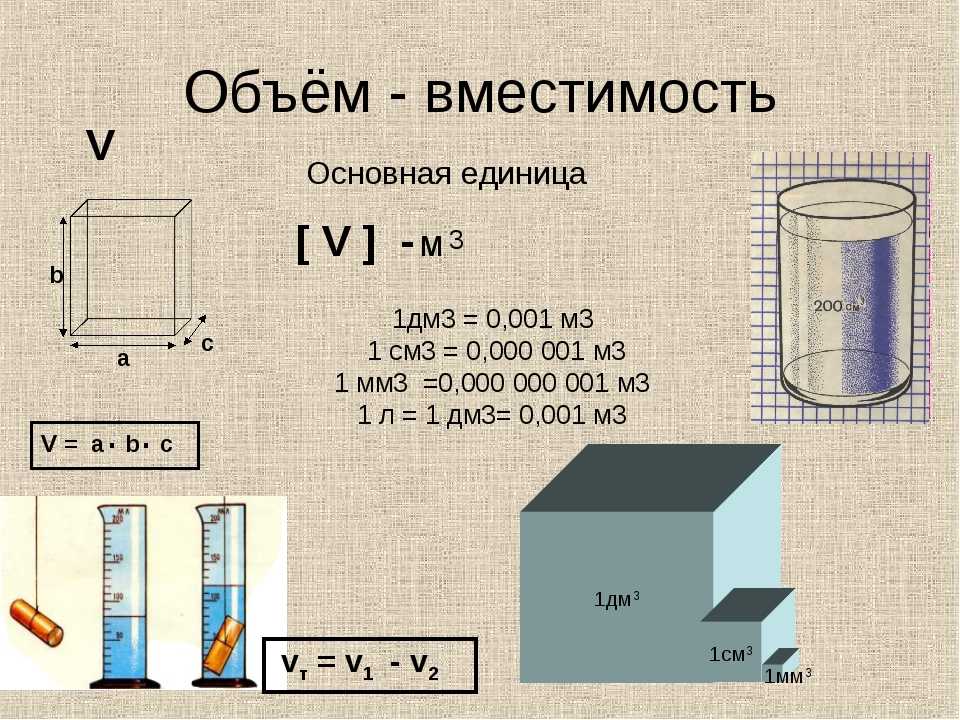
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м3 >;
зная равенство: 1 м3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Теория
Цилиндр может быть правильным или наклонным
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
[ LARGE V = S cdot H ]
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса
Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Формула расчета объема цилиндра
Объем цилиндра вычисляется как произведение площади основания на высоту цилиндра. Так как основанием цилиндра является круг, площадь основания можно рассчитать через радиус или диаметр.
Найти объем цилиндра
Выберите известные величины:
Введите данные:
| R | = |
| h | = |
Вводить можно числа или дроби (-2.4, 5/7, …).
Источники
- https://ru.onlinemschool.com/math/formula/volume/
- https://mnogoformul.ru/obem-cilindra
- https://poschitat.online/obem-cilindra
- https://MicroExcel.ru/obyom-tsilindra/
- https://www.
 calc.ru/obyem-tsilindra.html
calc.ru/obyem-tsilindra.html - https://gofro-karton.com/blog/rasschitat_obem_korobki/
- https://tara-tovara.ru/docs/poleznaya_inform/kak_rasschitat_obem_korobki_v_m3_i_litrakh/
- https://doza.pro/art/math/geometry/cylinder
- https://calcsbox.com/post/formula-obema-cilindra.html
- https://kalkulyator-nds.com/obem-cilindra-kalkulyator
- https://ru.onlinemschool.com/math/assistance/figures_volume/cylinder/
Калькулятор объема цилиндра
Автор: Ханна Памула, доктор философии
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 06 сентября 2022 г.
Содержание:- Как рассчитать объем цилиндра?
- Объем полого цилиндра
- Объем наклонного цилиндра
- Часто задаваемые вопросы
Наш калькулятор объема цилиндра позволяет вычислить объем этого твердого тела. Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другой вариант расчета объем цилиндрической оболочки (полый цилиндр).
Другой вариант расчета объем цилиндрической оболочки (полый цилиндр).
Как рассчитать объем цилиндра?
Начнем с самого начала – что такое цилиндр? Это твердое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Мы можем представить его как твердую физическую банку с крышками сверху и снизу. Для расчета его объема нам необходимо знать два параметра – радиус (или диаметр) и высоту:
объем цилиндра = π × радиус цилиндра² × высота цилиндра
Калькулятор объема цилиндра помогает найти объем прямого, полого и наклонного цилиндра:
Объем полого цилиндра
Полый цилиндр, также называемый цилиндрической оболочкой, представляет собой трехмерную область, ограниченную двумя прямыми круглыми цилиндрами. с одной осью и двумя параллельными кольцевыми основаниями, перпендикулярными общей оси цилиндров.
Легче понять это определение, представив, например, соломинку для питья или трубку – полый цилиндр – это пластик, металл или другой материал. Формула объема полого цилиндра:
Формула объема полого цилиндра:
объем_цилиндра = π × (R² - r²) × высота_цилиндра
где R – внешний радиус, а r – внутренний радиус
Для расчета объема цилиндрической оболочки возьмем пример из реальной жизни , может… рулон туалетной бумаги, а почему бы и нет? 😀
Введите внешний радиус цилиндра . Стандарт равен примерно 5,5 см.
Определить внутренний радиус цилиндра . Это внутренний радиус картонной детали около 2 см.
Узнать высоту цилиндра ; для нас это 9 см.
Тадаам! Объем полого цилиндра равен 742,2 см³.
Помните, что результатом является объем бумаги и картона. Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока!
Объем косого цилиндра
Косой цилиндр – это тот, который «наклоняется» – стороны не перпендикулярны основаниям, в отличие от стандартного «прямого цилиндра». Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Теперь, когда вы знаете, как рассчитать объем цилиндра, возможно, вы захотите определить объемы других трехмерных тел? Используйте этот общий калькулятор объема!
Если вам интересно, сколько чайных ложек или чашек поместится в ваш контейнер, воспользуйтесь нашим конвертером объема.
Для расчета объема грунта, необходимого для цветочных горшков различной формы, в том числе для цилиндрического, воспользуйтесь калькулятором грунта.
Часто задаваемые вопросы
Где можно найти цилиндры в природе?
Цилиндры вокруг нас , и мы говорим не только о банках Pringles. Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Они составляют большое количество природных объектов на Земле!
Они составляют большое количество природных объектов на Земле!
Как нарисовать цилиндр?
Чтобы нарисовать цилиндр, выполните следующие действия:
Нарисуйте слегка приплюснутый круг.
Начертить две равные параллельные линии с дальних сторон вашего круга спускается вниз.
Соедините концы двух линий полукруглой линией, которая выглядит так же, как нижняя половина вашего верхнего круга.
При необходимости добавьте тень и штриховку.
Как рассчитать вес цилиндра?
Для расчета веса баллона:
Возведение в квадрат радиуса цилиндра .
Умножьте квадрат радиуса на число пи и высоту цилиндра .
Умножьте объем на плотность цилиндра.
 Результат – вес цилиндра.
Результат – вес цилиндра.
Как рассчитать отношение площади поверхности к объему цилиндра?
Найдите объем цилиндра по формуле πr²h .
Найдите площадь поверхности цилиндра по формуле 2πrh + 2πr² .
Из двух формул составьте отношение , т. е. πr²h : 2πrh + 2πr².
В качестве альтернативы упростите его до rh : 2(h+r) .
Разделите с обеих сторон на одну из сторон, чтобы получить соотношение в его простейшей форме.
Как найти высоту цилиндра?
Если у вас объем и радиус цилиндра:
- Убедитесь, что объем и радиус указаны в тех же единицах , что и (например, см³ и см), а радиус — в радианах .
- Квадрат радиус.
- Разделите объем на квадрат радиуса и пи, чтобы получить высоту в тех же единицах, что и радиус.

Если у вас есть площадь поверхности и радиус (r):
- Убедитесь, что поверхность и радиус указаны в тех же единицах , что и , а радиус указан в радианах.
- Вычтите 2πr² из площади поверхности.
- Разделите результат шага 1 на 2πr.
- Результат — высота цилиндра.
Как найти радиус цилиндра?
Если у вас есть объем и высота цилиндра:
- Убедитесь, что объем и высота указаны в тех же единицах (например, см³ и см), а радиус указан в радианах .
- Разделить объем на пи и высоту.
- Квадрат корень результата.
Если у вас есть площадь поверхности и высота (h):
- Подставьте высоту, h и площадь поверхности в уравнение, площадь поверхности = πr²h : 2πrh + 2πr².

- Разделите с обеих сторон на 2π.
- Вычтите площади поверхности/2π с обеих сторон.
- Решите полученное квадратное уравнение.
- положительный корень — это радиус.
Как найти объем прямоугольного трапециевидного цилиндра?
Правильный трапециевидный цилиндр, также известный как прямоугольная призма , может быть решен следующим образом:
- Сложите вместе две параллельные стороны (основания) трапеции.
- Разделить результат на 2.
- Умножьте результат шага 2 на высоту трапеции (т.е. расстояние, разделяющее две стороны).
- Умножьте результат на длину цилиндра.
- Результатом является площадь правильного трапециевидного цилиндра.
Как найти объем овального цилиндра?
Чтобы найти объем овального цилиндра:
- Умножьте наименьший радиус овала (малая ось) на его наибольший радиус (большая ось).

- Умножьте это новое число на пи .
- Разделите результат шага 2 на 4. Результатом будет площадь овала.
- Умножьте площадь овала на высоту цилиндра.
- Результат — объем овального цилиндра.
Как найти объем наклонного цилиндра?
Чтобы вычислить объем наклонного цилиндра:
- Найдите радиус , длину стороны и угол наклона цилиндра.
- Квадрат радиус.
- Умножьте на число пи.
- Возьмем грех угла .
- Умножьте sin на длину стороны.
- Умножьте на результат шагов 3 и 5 вместе.
- В результате получается наклонный объем.
Как рассчитать рабочий объем цилиндра?
Чтобы вычислить рабочий объем цилиндра:
- Разделите диаметр отверстия на на 2, чтобы получить радиус отверстия .

- Квадрат радиус отверстия.
- Умножьте радиус квадрата на число пи.
- Умножьте результат шага 3 на длину штриха . Убедитесь, что единицы измерения диаметра и длины хода совпадают.
- Результатом является рабочий объем одного цилиндра.
Ханна Памула, PhD
Правый/наклонный полный цилиндр
Высота
Радиус
Диаметр
Том
Полый цилиндр
Высота
Диаметр Внешний
Диаметр Внутренний
Том
Проверьте 21 Аналогичные 3D -калькуляторы 📦 D.…
. далееОбъем цилиндра — формула, определение, решенные примеры
Объем цилиндра — это вместимость цилиндра, которая вычисляет количество материала, которое он может вместить. В геометрии есть формула определенного объема цилиндра, которая используется для измерения того, какое количество любой величины, будь то жидкость или твердое тело, может быть погружено в него равномерно. Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их:
Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их:
- Прямой круговой цилиндр: Цилиндр, основания которого представляют собой окружности, а каждый отрезок, являющийся частью боковой криволинейной поверхности, перпендикулярен основаниям.
- Наклонный цилиндр: Цилиндр, стороны которого опираются на основание под углом, не равным прямому углу.
- Эллиптический цилиндр: Цилиндр, основания которого представляют собой эллипсы.
- Прямой круглый полый цилиндр: Цилиндр, состоящий из двух правильных круглых цилиндров, заключенных один внутри другого.
| 1. | Объем цилиндра |
| 2. | Объем цилиндра Формула |
| 3. | Как рассчитать объем цилиндра? |
4. | Часто задаваемые вопросы об объеме цилиндра |
Каков объем цилиндра?
Объем цилиндра – это количество единичных кубов (кубов единичной длины), которые можно в него поместить. Это пространство, занимаемое цилиндром, поскольку объем любой трехмерной формы — это пространство, занимаемое им. Объем цилиндра измеряется в кубических единицах, таких как см 3 , m 3 , in 3 , и т. д. Посмотрим формулу, используемую для расчета объема цилиндра.
Определение цилиндра
Цилиндр представляет собой трехмерное твердое тело, состоящее из двух параллельных оснований, соединенных изогнутой поверхностью. Эти основания имеют форму круглого диска. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью цилиндра.
Объем цилиндра Формула
Мы знаем, что цилиндр похож на призму (но обратите внимание, что цилиндр не является призмой, так как имеет изогнутую боковую грань), мы используем ту же формулу объема призмы, чтобы вычислить объем цилиндра. Мы знаем, что площадь призмы вычисляется по формуле
Мы знаем, что площадь призмы вычисляется по формуле
V = A × h, где
- A = площадь основания
- ч = высота
Теперь применим эту формулу для расчета объема различных типов цилиндров.
Объем прямого круглого цилиндра
Мы знаем, что основанием правильного круглого цилиндра является окружность, а площадь окружности радиуса r равна πr 2 . Таким образом, объем (V) прямого кругового цилиндра по приведенной выше формуле равен
V = πr 2 h
цилиндр
Таким образом, объем цилиндра прямо зависит от его высоты и прямо зависит от квадрата его радиуса. т. е. если радиус цилиндра удвоится, то его объем удвоится.
Объем наклонного цилиндра
Формула для расчета объема цилиндра (наклонного) такая же, как и у прямого кругового цилиндра. Таким образом, объем (V) наклонного цилиндра с радиусом основания «r» и высотой «h» равен
V = πr 2 h
Объем эллиптического цилиндра
Мы знаем, что эллипс имеет два радиуса. Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен
Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен
V = πabh
Здесь
- ‘a’ и ‘b’ — радиусы основания (эллипса) цилиндра.
- ‘h’ — высота цилиндра.
- π — это константа, значение которой равно 22/7 (или) 3,142.
Объем прямого кругового полого цилиндра
Поскольку правильный круговой цилиндр представляет собой цилиндр, состоящий из двух правильных круговых цилиндров, заключенных один внутри другого, его объем получается путем вычитания объема внутреннего цилиндра из объема внешнего цилиндра. . Таким образом, объем (V) прямого круглого полого цилиндра равен
V = π(R 2 — r 2 )h
Здесь
- ‘R’ — радиус основания внешнего цилиндра. .
- ‘r’ — радиус основания внутреннего цилиндра.
- ‘h’ — высота цилиндра.
- π — это константа, значение которой равно 22/7 (или) 3,142.

Как рассчитать объем цилиндра?
Вот шагов для вычисления объема цилиндра:
- Определите радиус как ‘r’ и высоту как ‘h’ и убедитесь, что они имеют одинаковые единицы измерения.
- Подставить значения в формулу объема V = πr 2 ч.
- Запишите единицы измерения в кубических единицах.
Пример: Найдите объем прямоугольного цилиндра радиусом 50 см и высотой 1 метр. Используйте π = 3,142.
Решение:
Радиус цилиндра равен r = 50 см.
Высота: h = 1 метр = 100 см.
Его объем V = πr 2 h = (3,142)(50) 2 (100) = 785 500 см 3 .
Примечание: Нам нужно использовать формулу, чтобы найти объем цилиндра в зависимости от его типа, как мы обсуждали в предыдущем разделе. Кроме того, предположим, что цилиндр является правильным круговым цилиндром, если не указан тип, и примените формулу объема: V = πr 2 ч.
Объем цилиндра Примеры
Пример 1: Найдите объем цилиндрического резервуара для воды с радиусом основания 25 дюймов и высотой 120 дюймов. Используйте π = 3,14.
Решение:
Радиус цилиндрического резервуара r = 25 дюймов.
Его высота h = 120 дюймов.
Используя формулу объема цилиндра, объем резервуара равен
V = πr 2 ч
V = (3,14)(25) 2 (120) = 235500 кубических дюймов.
Ответ: Объем данного цилиндрического резервуара составляет 235 500 кубических дюймов.
Пример 2: Найдите объем эллиптического цилиндра, радиусы основания которого 7 дюймов и 10 дюймов, а высота 15 дюймов. Используйте π = 22/7.
Решение:
Радиусы основания данного эллиптического цилиндра равны
a = 7 дюймов и b = 10 дюймов.
Его высота h = 15 дюймов.
Используя формулу объема цилиндра, объем данного эллиптического цилиндра равен
V = πabh
V = (22/7) × 7 × 10 × 15 = 3300 кубических дюймов.

Ответ: Объем данного цилиндра составляет 3300 кубических дюймов.
Пример 3: Каков объем цилиндра с радиусом 4 единицы и высотой 6 единиц?
Решение:
Радиус,r = 4 ед. Высота,h = 6 ед.
Объем цилиндра, V = πr 2 h кубических ед.
В = (22/7) × (4) 2 × 6 В = 22/7 × 16 × 6
В = 301,71 кубических единиц.
Следовательно, объем цилиндра равен 301,71 куб.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.
Записаться на бесплатный пробный урок
Практические вопросы по объему цилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме цилиндра
Каков объем цилиндра?
Объем цилиндра — это количество свободного места в нем. Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 час.
Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 час.
Какая формула для расчета объема цилиндра?
Формула для расчета объема цилиндра: V = πr 2 h, где
- ‘r’ — радиус основания цилиндра
- ‘h’ — высота цилиндра
- π — это константа, значение которой равно 22/7 (или) 3,142.
Каков объем цилиндра с диаметром?
Рассмотрим цилиндр радиуса «r», диаметра «d» и высоты «h». Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 час. Мы знаем, что r = d/2. Подставив это в приведенную выше формулу, V = πd 2 ч/4.
Каково соотношение объемов цилиндра и конуса?
Рассмотрим цилиндр и конус, каждый из которых имеет радиус основания ‘r’ и высоту ‘h’. Мы знаем, что объем цилиндра равен πr 2 ч, а объем конуса равен 1/3 πr 2 ч. Таким образом, требуемое соотношение равно 1:(1/3) (или) 3:1.
Как найти объем цилиндра по диаметру и высоте?
Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен, V = πr 2 h. Если диаметр основания равен d, то d = r/2. Подставляя это в приведенную выше формулу, мы получаем V = πd 2 ч/4. Таким образом, формула для нахождения объема цилиндра с диаметром (d) и высотой (h) имеет вид V = πd 2 ч/4.
Как найти объем цилиндра с окружностью и высотой?
Мы знаем, что длина окружности радиуса r равна C = 2πr. Таким образом, когда длина окружности основания цилиндра (C) и его высота (h) заданы, мы сначала решаем уравнение C = 2πr для ‘r’, а затем применяем формулу объема цилиндра, то есть V = πr 2 час.
Как рассчитать объем цилиндра в литрах?
Мы можем использовать следующие формулы преобразования, чтобы преобразовать объем цилиндра из м 3 (или) см 3 в литры.
- 1 м 3 = 1000 литров
- 1 см 3 = 1 мл (или) 0,001 литра
☛ Чек:
- Преобразование в метрическую систему
- Преобразование единиц измерения
Что произойдет с объемом цилиндра, если его радиус уменьшить вдвое?
Объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 th .
Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 th .
Что происходит с объемом цилиндра, когда его радиус увеличивается вдвое?
Мы знаем, что объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус увеличивается вдвое, объем увеличивается в четыре раза.
Как найти объем цилиндра с помощью калькулятора?
Калькулятор объема цилиндра — это машина для расчета объема цилиндра. Чтобы рассчитать объем цилиндра с помощью калькулятора, нам нужно предоставить необходимые данные для инструмента калькулятора, такие как требуемые размеры, такие как радиус, диаметр, высота и т. д. Попробуйте теперь вычислить объем цилиндра, введите радиус и высоту цилиндра. в данном ящике объема цилиндра калькулятор. Нажмите на кнопку «Рассчитать», чтобы найти объем цилиндра. Нажав кнопку «Сбросить», вы можете легко очистить ранее введенные данные и найти объем цилиндра для разных значений.
☛ Чек:
- Калькулятор цилиндров
- Калькулятор площади поверхности цилиндра
- Калькулятор высоты цилиндра
Что такое площадь и объем цилиндра?
Площадь поверхности цилиндра – это общая площадь или область, покрываемая поверхностью цилиндра. Площадь поверхности цилиндра определяется двумя следующими формулами:
Площадь поверхности цилиндра определяется двумя следующими формулами:
- Площадь криволинейной поверхности цилиндра = 2πrh
- Общая площадь поверхности цилиндра = 2πr 2 +2πrh = 2πr(h+r)
Площадь цилиндра выражается в квадратных единицах, например, в м 2 , в 2 , см 2 , ярдах 2 и т. д.
в цилиндре, который можно рассчитать по формуле объема цилиндра V = πr 2 ч. Объем цилиндра всегда измеряется в кубических единицах.
☛ Проверить:
- Площадь поверхности цилиндра Листы
- Объем цилиндра Рабочие листы
- Формулы площади поверхности
Как изменится объем полого цилиндра при удвоении высоты?
Формула объема полого цилиндра равна V = π(R 2 — r 2 )h кубических единиц. Из формулы объема видно, что объем прямо пропорционален высоте полого цилиндра. Следовательно, объем удваивается, когда высота полого цилиндра удваивается.

 Как посчитать объем цилиндра
Как посчитать объем цилиндра 2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту: 14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3 Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.