Процесс сжатия: Процесс сжатия

Содержание

Процесс сжатия

Процесс сжатия

Процесс сжатия в двигателях внутреннего сгорания служит для создания лучших условий сгорания рабочей смеси, а также для увеличения температурного перепада цикла и степени расширения продуктов сгорания. Это создает благоприятные условия для увеличения КПД двигателя.

Процесс сжатия изображается на индикаторной диаграмме линией. В начальный период сжатия температура газов ниже температуры стенок цилиндра, поэтому газы дополнительно нагреваются от них. По мере сжатия смеси ее температура повышается и теплопередача от стенок цилиндра к газам уменьшается. В какой-то бесконечно малый период времени температуры газов и отенок цилиндра будут равны и теплообмена не будет. Дальнейшее сжатие происходит с отводом тепла от газов к стенкам цилиндра.

Процесс сжатия протекает в условиях непрерывного изменения температуры рабочей смеси или воздуха. Теплообмен имеет сложный характер и не может быть выражен точно при помощи термодинамических соотношений, поэтому считают, что весь процесс сжатия протекает поли-тропно с постоянным показателем nv

Рекламные предложения на основе ваших интересов:

Дополнительные материалы по теме:

Данные испытаний показывают, что показатель политропы пх имеет различные значения для различных двигателей и для одного и того же двигателя изменяется с изменением режима и условий его работы. Его значение будет тем больше, чем больше объем цилиндра, так как при этом меньше относительная площадь охлаждения. При интенсивном охлаждении увеличивается теплоотдача от газов к стенкам цилиндра и, следовательно, снижается величина показателя nv С повышением частоты вращения коленчатого вала время соприкосновения газов со стенками цилиндра за период сжатия сокращается и показатель политропы п1 увеличивается. Кроме того, величина пх зависит от продолжительности открытия впускного клапана, опережения зажигания и других факторов. Среднее значение показателя политропы сжатия пх для карбюраторных двигателей колеблется в пределах 1,32—1,39, для дизельных 1,36—1,40.

Давление рс и температура Тс в конце сжатия тем выше, чем больше степень сжатия е и средний показатель политропы, в результате чего выше мощность и экономичность двигателя.

—

Основное назначение процесса сжатия состоит в том, чтобы создать условия, способствующие возможно лучшему сгоранию горючей смеси.

Процесс сжатия протекает в условиях непрерывного изменения температуры заряда и теплообмена между зарядом, стенками цилиндра и днищем поршня.

В начале сжатия, при установившемся тепловом режиме двигателя, температура заряда ниже температуры стенок цилиндра и днища поршня, поэтому заряд подогревается при соприкосновении с ними. Дальнейшее сжатие заряда приводит к повышению его температуры, в результате чего тепло передается от заряда к стенкам цилиндра и к днищу поршня. Поэтому процесс сжатия характеризуется политропным изменением параметров заряда.

ᐉ Процесс сжатия топлива

Свежий заряд с примесью остаточных газов после процесса впуска подергается сжатию.

Назначение процесса сжатия:

увеличение температурного перепада, при котором осуществляется действительный цикл;
улучшение воспламенения и горения топлива;
получение большей работы при расширении продуктов сгорания и повышение экономичности двигателя.

Процесс сжатия происходит при движении поршня от НМТ к ВМТ после закрытия впускного клапана. Но если в термодинамических циклах сжатие происходило без теплообмена (адиабатическое сжатие), то в действительных циклах этот процесс сопровождается непрерывным, переменным по величине и направлению теплообменом между рабочим телом и окружающими ею деталями, частичной потере рабочею тела через неплотности в сопряжениях деталей и испарением части находящегося в цилиндре в капельножидком состоянии топлива.

Таким образом, процесс сжатия носит политропный характер.

Рис. Зависимости изменения давления (а) и показателя политропы сжатия (б) от объема полости цилиндра

В начале сжатия происходит теплопередача от деталей к рабочему телу, так как температура Та рабочего тела в этот момент ниже температуры стенок полости цилиндра. В результате кривая процесса сжатия в р—V координатах проходит несколько круче кривой адиабатного сжатия, и показатель n1 политропы сжатия больше показателя к адиабаты сжатия.

При дальнейшем сжатии температура рабочего тела увеличивается, и теплообмен между рабочим телом и окружающими его деталями снижается. В какой-то момент температура рабочего тела становится равной температуре стенок цилиндра, и наступает мгновенный адиабатный процесс. Показатели политропы и адиабаты сжатия становятся равными: n1 = к (точка d).

При продолжении сжатия температура рабочего тела становится выше средней температуры окружающих его деталей, и теплота начинает переходить от рабочего тела к деталям двигателя.

В этом случае кривая сжатия проходит выше кривой адиабаты сжатия, n1 < к. Причем разность значений увеличивается по мере приближения поршня к ВМТ.

При расчетах использовать переменные значения показателя политропы затруднительно. Поэтому применяют постоянное значение показателя n1, которое находится от 1,2 до 1,4 и называется средним. Большие значения показатель политропы сжатия принимает при более высоких частотах вращения коленчатого вала, при этом процесс сжатия приближается к адиабатному. Это же наблюдается и при увеличении размеров цилиндра. так как уменьшается относительная величина поверхности охлаждения цилиндра. По этим же причинам пуск двигателей с небольшими габаритными размерами цилиндров вызывает определенные сложности.

Величина относительной поверхности охлаждения цилиндра показывает значительное влияние на теплообмен, а значит и на показатель n1 в процессе сжатия, которая представляет собой отношение площади контактной поверхности рабочего тела и деталей в процессе сжатия к рабочему объему цилиндра.

При неизменном рабочем объеме цилиндров относительная величина поверхности охлаждения уменьшается с увеличением диаметра цилиндра. Поэтому чем диаметр D больше хода поршня S, тем больше значение среднего показателя политропы сжатия.

Значения n1 увеличиваются при использовании наддува и алюминиевых сплавов вместо чугуна при изготовлении деталей цилиндропоршневой группы, а также камеры сгорания небольших габаритных размеров.

При износе цилиндропоршневой группы возрастают утечки рабочего тела, и значения n1 уменьшаются. Этим объясняются затруднения пуска при значительных износах деталей двигателя.

Posted in Двигатель автомобиляTagged Сжатие, Топливо

Изэнтропическое сжатие или расширение

Термодинамика — это раздел физики который имеет дело с энергией и работой системы. Термодинамика занимается только широкомасштабный ответ системы, которую мы можем наблюдать и измерять в опытах. В аэродинамике мы больше всего интересуется термодинамикой из-за той роли, которую она играет в конструкция двигателя и потоки с высокой скоростью.

На этом слайде мы выводим два важных уравнения, которые связывают давление, температура, и объем которое занимает газ при обратимом сжатии или расширении. Такой процесс происходит во время компрессия и силовые удары для двигатель внутреннего сгорания. Одни и те же уравнения описывают условия в компрессор и турбина из газотурбинный двигатель. Например, двигатель внутреннего сгорания. мы показываем компьютерный чертеж одного цилиндр Райт 1903 двигатель вверху слева. Движение серого поршня внутри синего цилиндр поворачивает красную часть коленчатый вал который превращает пропеллеры для создания тяги. При движении поршня в цилиндре объем топливно-воздушной газовой смеси внутри цилиндра меняется. Это изменение объема приводит к изменению давление и температура газа, которые определяют, насколько работа поршень может поставить.

При движении поршня будем считать, что нет нагревать переносится в цилиндр. Мы в дальнейшем будем пренебрегать любым трения между поршнем и цилиндром и считать, что нет потери энергии любого рода. (В реальности небольшие потери и мы учитывать потери с помощью «коэффициента эффективности», применяемого к результату получаем без потерь.) В результате сжатия и расширения обратимые процессы в которой энтропия системы остается постоянной. Мы можем использовать уравнения для энтропии чтобы связать потоковые переменные системы.

Начнем наш вывод с определения значения фактора, который мы нужно позже. Из определений коэффициенты удельной теплоемкости, удельная теплоемкость при постоянном давлении

сП минус удельная теплоемкость при постоянном объеме cv равна газовая постоянная R:

ср — ср = R

и мы определяем отношение удельных теплоемкостей как число, которое мы позвонит «гамма»

гамма = cp/cv

Если мы разделим первое уравнение на cp и воспользуемся определением «гамма» мы получаем:

R / cp = 1 — (1 / гамма) = (гамма — 1) / гамма

Теперь воспользуемся уравнением, которое мы вывели для энтропия газа:

s2 — s1 = cp ln(T2 / T1) — R ln(p2 / p1)

где цифры 1 и 2 обозначают состояния в начале и в конце процесс сжатия, с – энтропия, T – температура, р — давление, а «ln» обозначает натуральный логарифм функция.

Так как в цилиндр не передается теплота и нет других потерь, изменение энтропии равно нулю. Тогда уравнение становится:

cp ln(T2 / T1) = R ln(p2 / p1)

Мы разделим обе части на «cp» и возьмем экспоненциальную функцию обе стороны (это «отменяет» логарифмы). 9[(гамма — 1)/гамма]

В процессе сжатия по мере увеличения давления от p1 до p2, температура увеличивается от T1 до T2 согласно этому экспоненциальному закону уравнение. «Гамма» — это просто число, которое зависит от газа. Для воздуха, на стандартные условия, это 1,4. Значение (1 — 1/гамма) составляет около 0,286. Таким образом, если давление увеличилось вдвое, отношение температур равно 1,219. Ключевым моментом здесь является то, что у нас есть функция, которая связывает температуру изменение на изменение давления в процессе сжатия. 9(гамма)

Количество (v1 / v2)

является соотношение объема в состоянии 1 и состоянии 2 и называется степенью сжатия .

Для v2 меньше, чем v1 , давление p2 больше, чем стр1 . С помощью этого уравнения мы можем определить изменение давления при заданной степени сжатия. И используя предыдущий уравнения мы знаем также изменение температуры. Значение степени сжатия является функцией конструкции отверстие и ход поршня.

Деятельность:

Экскурсии с гидом

Навигация..

Домашняя страница руководства для начинающих

Конспекты лекций Джона Штрауба

Термодинамика сжатия или расширения идеального газа

Ингредиенты: манометр, шприц

Процедура:

1. Поместите фиксированное количество газа в шприц.

2. Варьировать объем газа в шприце, наблюдая за изменением давления.

3. Проанализируйте количество теплоты, подведенное к газу, работу, совершенную над газом, а также изменение энергии и энтальпии газа.

Понимание: Идеальный газ — одна из немногих моделей химических процессов, в которой у нас есть полное знание термодинамики системы. У нас есть уравнение состояния, PV=nRT. Для простого атомарного идеального газа у нас также есть точное выражение для внутренней энергии E=(3/2)nRT. Идеальный газ дает нам возможность вычислить весь набор свойств первого закона, от изменений энергии и энтальпии до теплоты и работы.

В экспериментальном процессе газ изотермически сжимают от начального давления 1,0 атмосферы и объема 30,0 мл до конечного давления 3,0 атмосферы и объема 10,0 мл. Температура на всем протяжении 20,0С. Изотермическое сжатие газа осуществлялось двумя способами: необратимым и обратимым.

Необратимое изотермическое сжатие

Необратимое сжатие газа происходит в одну стадию при постоянном внешнем давлении 3,0 атм.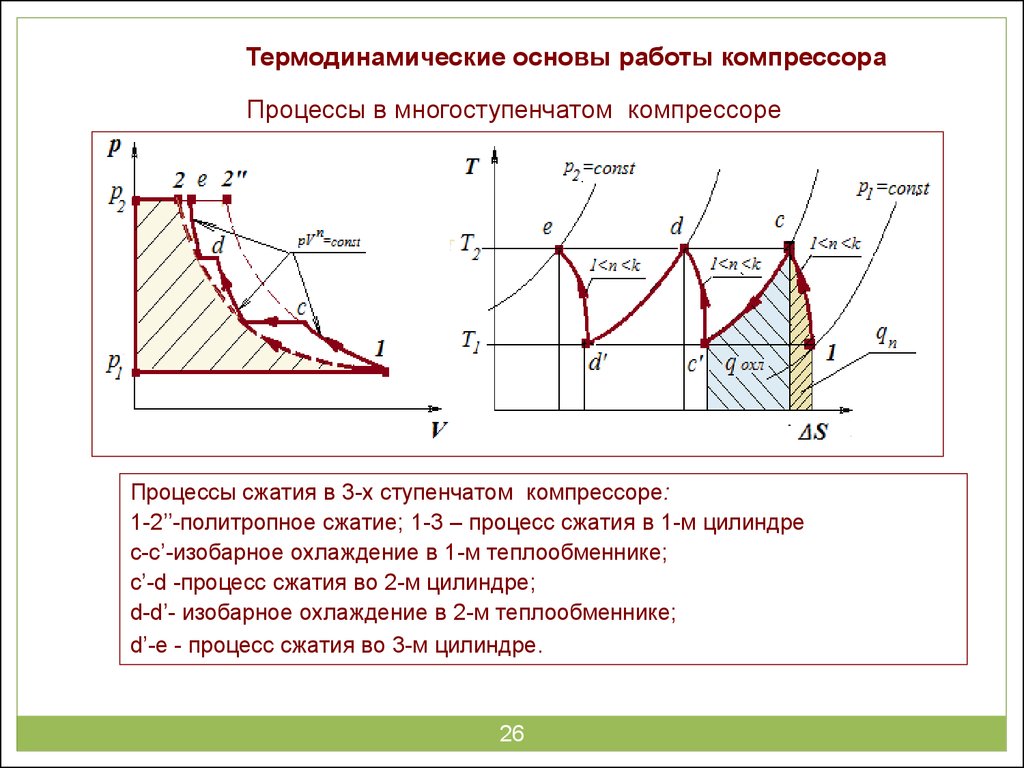 Работа предоставлена

w = -P _доб ΔV = 0,060 лат.

над

Как вычислить количество теплоты, переданное газу? Косвенно! Отметим, что процесс изотермический. Полная энергия идеального газа равна

ΔE = n c _В ΔT

ΔE = q + w

Теплота, подведенная к системе, отрицательна, потому что газ сжимается. Почему? При отсутствии теплообмена газ приобретет внутреннюю энергию при сжатии и его температура повысится. Чтобы поддерживать постоянную температуру газа, газ должен передавать положительное количество тепла в окружающую среду. Таким образом, тепло, добавленное 90 160 к 90 161 сжатому газу, имеет отрицательное значение, поддерживая постоянную температуру.

Наконец, для идеального газа

ΔH = n c _P ΔT

а поскольку температура постоянна, ΔT=0, отсюда следует, что ΔH=0.
Реверсивное изотермическое сжатие
Обратимое сжатие газа происходит за бесконечное число бесконечно малых шагов, при этом приложенное внешнее давление всегда практически равно внутреннему давлению газа (или больше лишь на бесконечно малую величину). Работа предоставлена
w = -nRT ln(V ₂ /V ₁ ) = -(0,030 лат) ln(0,010 л/0,030 л) = 0,033 лат.
Работа, совершаемая над газом, положительна, поскольку газ сжимается; окружение совершает положительную работу над газом. Обратите внимание, что работа, совершаемая над газом, больше для необратимого процесса.
w _irr > w _ред.
что верно в целом.
Мы вычисляем теплоту, присоединенную к газу, так же, как и для необратимого процесса. Косвенно! Снова изменение энергии системы для изотермического процесса равно
ΔЕ = 0
и имеем q=-w=-0,033 лат.
Заметим, что изменение энергии должно быть одинаковым для обратимого и необратимого процессов, поскольку начальное и конечное состояния газа одинаковы. Поскольку изменение энергии зависит только от начального и конечного состояний системы, оно не зависит от пройденного пути. Отсюда следует, что ΔH=0.
Обратимое адиабатическое сжатие
В адиабатическом процессе теплота, подведенная к системе, равна нулю или
д=0
Предположим, что у нас есть идеальный газ с начальной температурой 20,0°С, давлением 1,0 атмосферы и объемом 30,0 мл. Газ адиабатически сжимают до объема 10,0 мл. Давайте вычислим величины первого закона, q, w, ΔE и ΔH.
Из определения адиабатического процесса имеем q=0. Как вычислить изменение энергии системы? Мы не можем сделать это, вычислив работу, проделанную системой. Нам нужно определить изменение энергии системы, а затем вычислить работу, совершенную системой по первому закону.
Изменение энергии системы равно
ΔE = n c _В ΔT
Чтобы вычислить изменение энергии системы, нам нужно знать конечную температуру газа. Мы можем вычислить эту температуру, используя соотношение
T ₁ V ₁ ^{c _P /c _V -1} = T ₂ V ₂ ^{c _P /c _V -1}
которое справедливо для обратимого адиабатического расширения или сжатия идеального газа.
Нам известны начальный и конечный объемы, известна начальная температура. Мы можем вычислить конечную температуру, которая равна 609K. Затем можно вычислить изменение энергии, используя тот факт, что для этого простого идеального газа
c _В = (3/2) R
так что ΔE=nc _В ΔT = (3/2)nRΔT=0,049 лат.
Из первого начала термодинамики следует, что w=ΔE-q=ΔE=0,049 лат. Это имеет смысл. При сжатии газа совершается положительная работа на газ.
Наконец, мы знаем, что для любого идеального газа
ΔH = n c _P ΔT
а также верно для любого идеального газа, который
с _Р =с _В + Р
Для этого адиабатического процесса ΔH=0,081 лат.