Q лямбда м: Q=лямбда. Как называется формула ?(физика)

Содержание

Придумайте задачу по формуле Q=Lm , Q= лямбда • m… -reshimne.ru

Новые вопросы

Ответы

Медь, взятая при температуре 40 градусов, массой 5 кг начали плавить. Сколько на это потребуется энергии?
Сколько потребуется энергии для того, чтобы испарить весь эфир массой 10 кг?

просто и доходчиво – формула, таблица

Оставить комментарий

Содержание:

Почему твердое тело становится жидким?

Определение

Единица измерения

Таблица удельной теплоты плавления

Рекомендованная литература и полезные ссылки

Видео

Под плавлением в физике подразумевают процесс превращения тела из твердого состояния в жидкое, под действием температуры. Классическим повсеместным примером плавления из жизни является таяние льдов, их превращение в воду, или превращение твердого куска олова в жидкий припой под действием паяльника. Передача тому или иному телу определенного количества тепла может изменить его агрегатное состояние, это удивительное свойство твердых тел превращаться в жидкие под действием температуры имеет большое значение для науки и техники. Ученым (а также техникам, инженерам) важно знать при каких температурах плавятся те или иные металлы (а порой и не только металлы), и для этого в физику вошло такое понятие как «удельная теплота плавления». О том, что означает удельная теплота плавления, какая ее формула расчета, читайте далее.

Почему твердое тело становится жидким?

Но давайте для начала разберем, как происходит сам процесс плавления на атомно-молекулярном уровне. Как мы знаем, в любом твердом теле все атомы и молекулы находятся четко и упорядочено в узлах кристаллической решетки, благодаря этому твердое тело и является твердым.

Но что происходит, если мы начинает это самое гипотетическое твердо тело сильно нагревать – под действием температуры атомы и молекулы резко увеличивают свою кинетическую энергию и по достижении определенных критических значений, они начинают покидать кристаллическую решетку, вырываться из нее. А само твердое тело начинает буквально распадаться, превращаясь в некое жидкое вещество – так происходит плавление.

При этом процесс плавления происходит не резким скачком, а постепенно. Также стоит заметить, что плавление относится к эндотермическим процессам, то есть процессам, при которых происходит поглощение теплоты.

Процесс обратный к плавлению называют кристаллизацией – это когда тело из жидкого состояния наоборот превращается в твердое. Если вы оставите воду в морозилке, она через какое-то время превратится в лед – это самый типичный пример кристаллизации из реальной жизни.

Определение

Удельной теплотой плавления называют физическую величину равную количеству тепла (в джоулях), которое необходимо передать твердому телу массой 1 кг, чтобы полностью перевести его в жидкое состояние. Удельную теплоту плавления обозначают греческой буквой «лямбда» – λ.

Формула удельной теплоты плавление выглядит так:

λ = Q/m

Где m – масса плавящегося вещества, а Q – количество тепла, переданное веществу при плавлении.

Зная значение удельной теплоты плавления, мы можем определить, какое количество тепла необходимо передать для тела с той или иной массой, для его полного расплавления:

Q = λ * m

Для разных веществ удельная теплота плавления была определена экспериментально.

Единица измерения

Многих интересует вопрос, в каких единицах измеряется удельная теплота плавления. Так вот, удельная теплота плавления измеряется в Джоулях на килограмм – Дж/кг.

Таблица удельной теплоты плавления

Значение удельной теплоты для разных веществ: золота, серебра, цинка, олова и многих других металлов можно найти в специальных таблицах и справочниках. Обычно эти значения приводятся в виде таблицы.

Вашему вниманию таблица удельной теплоты плавления разных веществ

Вещество	*10⁵ Дж/кг**	ккал/кг	Вещество	*10⁵ Дж/кг**	ккал/кг
Алюминий	3,8	92	Ртуть	0,1	3,0
Железо	2,7	65	Свинец	0,3	6,0
Лед	3,3	80	Серебро	0,87	21
Медь	1,8	42	Сталь	0,8	20
Нафталин	1,5	36	Цинк	1,2	28
Олово	0,58	14	Платина	1,01	24,1
Парафин	1,5	35	Золото	0,66	15,8

Интересный факт: самым тугоплавким металлом на сегодняшний день является карбид тантала – ТаС.

Для его плавления необходима температура 3990 С. Покрытия из ТаС применяют для защиты металлических форм, в которых отливают детали из алюминия

Видео

Автор: Павел Чайка, главный редактор журнала Познавайка

При написании статьи старался сделать ее максимально интересной, полезной и качественной.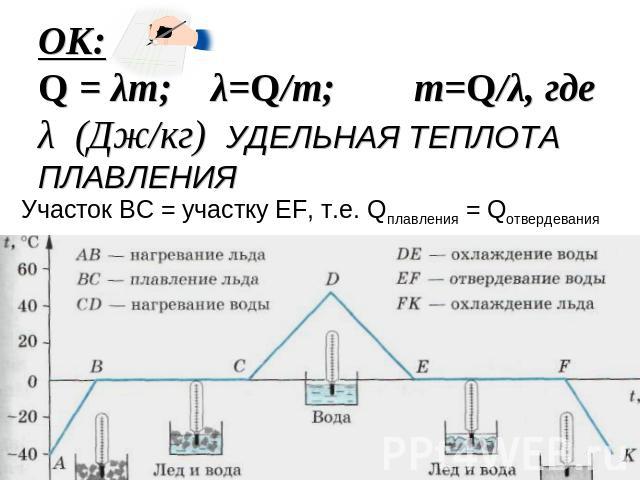 Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.

Страница про автора

Эта статья доступна на английском языке – Enthalpy of Fusion.

Формула количества теплоты в физике

Содержание:

Определение и формула количества теплоты
Формула расчета теплоты при изменении температуры
Формула количества теплоты при фазовых переходах
Единицы измерения количества теплоты
Примеры решения задач

Определение и формула количества теплоты

Внутреннюю энергию термодинамической системы можно изменить двумя способами:

совершая над системой работу,
при помощи теплового взаимодействия.

Передача тепла телу не связана с совершением над телом макроскопической работы. В данном случае изменение внутренней энергии вызвано тем, что отдельные молекулы тела с большей температурой совершают работу над некоторыми молекулами тела, которое имеет меньшую температуру. В этом случае тепловое взаимодействие реализуется за счет теплопроводности. Передача энергии также возможна при помощи излучения. Система микроскопических процессов (относящихся не ко всему телу, а к отдельным молекулам) называется теплопередачей. Количество энергии, которое передается от одного тела к другому в результате теплопередачи, определяется количеством теплоты, которое предано от одного тела другому.

Определение

Теплотой называют энергию, которая получается (или отдается) телом в процессе теплообмена с окружающими телами (средой). Обозначается теплота, обычно буквой Q.

Это одна из основных величин в термодинамике. Теплота включена в математические выражения первого и второго начал термодинамики. Говорят, что теплота – это энергия в форме молекулярного движения.

Теплота может сообщаться системе (телу), а может забираться от нее. Считают, что если тепло сообщается системе, то оно положительно.

Формула расчета теплоты при изменении температуры

Элементарное количество теплоты обозначим как $\delta Q$. Обратим внимание, что элемент тепла, которое получает (отдает) система при малом изменении ее состояния не является полным дифференциалом. Причина этого состоит в том, что теплота является функцией процесса изменения состояния системы.

Элементарное количество тепла, которое сообщается системе, и температура при этом меняется от Tдо T+dT, равно:

$$\delta Q=C d T(1)$$

где C – теплоемкость тела. Если рассматриваемое тело однородно, то формулу (1) для количества теплоты можно представить как:

$$\delta Q=c m d T=\nu c_{\mu} d T(2)$$

где $c=\frac{C}{m}$ – удельная теплоемкость тела, m – масса тела, $c_{\mu}=c \cdot \mu$ — молярная теплоемкость, $\mu$ – молярная масса вещества, $\nu=\frac{m}{\mu}$ – число молей вещества.

Если тело однородно, а теплоемкость считают независимой от температуры, то количество теплоты ($\Delta Q$), которое получает тело при увеличении его температуры на величину $\Delta t = t_2 — t_1$ можно вычислить как:

$$\Delta Q=c m \Delta t(3)$$

где t₂, t₁ температуры тела до нагрева и после. Обратите внимание, что температуры при нахождении разности ($\Delta t$) в расчетах можно подставлять как в градусах Цельсия, так и в кельвинах.

Формула количества теплоты при фазовых переходах

Переход от одной фазы вещества в другую сопровождается поглощением или выделением некоторого количества теплоты, которая носит название теплоты фазового перехода.

Так, для перевода элемента вещества из состояния твердого тела в жидкость ему следует сообщить количество теплоты ($\delta Q$) равное:

$$\delta Q=\lambda d m$$

где $\lambda$ – удельная теплота плавления, dm – элемент массы тела. При этом следует учесть, что тело должно иметь температуру, равную температуре плавления рассматриваемого вещества. При кристаллизации происходит выделение тепла равного (4).

Количество теплоты (теплота испарения), которое необходимо для перевода жидкости в пар можно найти как:

$$\delta Q=r d m$$

где r – удельная теплота испарения. При конденсации пара теплота выделяется. Теплота испарения равна теплоте конденсации одинаковых масс вещества.

Единицы измерения количества теплоты

Основной единицей измерения количества теплоты в системе СИ является: [Q]=Дж

Внесистемная единица теплоты, которая часто встречается в технических расчетах. [Q]=кал (калория). 1 кал=4,1868 Дж.

Примеры решения задач

Пример

Задание. Какие объемы воды следует смешать, чтобы получить 200 л воды при температуре t=40С, если температура одной массы воды t₁=10С, второй массы воды t₂=60С?

Решение. Запишем уравнение теплового баланса в виде:

$$Q=Q_{1}+Q_{2}(1.1)$$

где Q=cmt – количество теплоты приготовленной после смешивания воды; Q₁=cm₁t₁ — количество теплоты части воды температурой t₁ и массой m₁; Q₂=cm₂t₂— количество теплоты части воды температурой t₂ и массой m₂.

Из уравнения (1.1) следует:

$$ \begin{array}{l} \mathrm{cmt}=\mathrm{cm}_{1} t_{1}+\mathrm{~cm}_{2} t_{2} \rightarrow \mathrm{mt}=\mathrm{m}_{1} t_{1}+\mathrm{~m}_{2} t_{2} \rightarrow \\ \rightarrow \rho \mathrm{Vt}=\rho V_{1} t_{1}+\rho \mathrm{V}_{2} t_{2} \rightarrow \mathrm{Vt}=V_{1} t_{1}+V_{2} t_{2}(1.2) \end{array} $$

При объединении холодной (V₁) и горячей (V₂) частей воды в единый объем (V) можно принять то, что:

$$$ V=V_{1}+V_{2}(1. 3) $$$

Так, мы получаем систему уравнений:

$$ \left\{\begin{array}{c} V t=V_{1} t_{1}+V_{2} t_{2} \\ V=V_{1}+V_{2} \end{array}\right. $$

Решив ее получим:

$$ \begin{array}{l} V_{1}=\frac{\left(t_{2}-t\right)}{t_{2}-t_{1}} V \\ V_{2}=\frac{\left(t-t_{1}\right)}{t_{2}-t_{1}} V \end{array} $$

Проведем вычисления (это можно сделать, не переходя в систему СИ):

$$ \begin{array}{l} V_{1}=\frac{(60-40)}{60-10} 200=80 \text { (л) } \\ V_{2}=\frac{(40-10)}{60-10} 200=120 \text { (л) } \end{array} $$

Ответ. V₁=80 л, V₂=120 л.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. {*}\right) \end{array} $$

Ответ. $\Delta Q$=1700 Дж

Читать дальше: Формула напряженности магнитного поля.

Обозначение функций – Основы – документация по kdb+ и q

Обозначение функций позволяет определять функции. Обозначение функции также известно как лямбда-нотация , а определенные функции — как лямбда-выражения .

Анонимность

Хотя термин лямбда возник в другом месте как имя анонимной функции, мы используем его для обозначения любой функции, определенной с использованием лямбда-нотации.

В этом случае лямбда, которой присвоено имя, остается лямбдой. Например, если plus:{x+y} , тогда плюс — это лямбда.

Лямбды имеют тип данных 100.

Лямбда определяется как пара фигурных скобок (фигурных скобок), заключающая в себе необязательную подпись (список до 8 имен аргументов), за которой следует ноль или более выражений, разделенных точкой с запятой.

 q){[a;b] a2:a*a; б2:б*б; a2+b2+2*a*b}[20;4] / бинарная функция
576

Функции с 3 или менее аргументами могут не указывать сигнатуру и вместо этого использовать имена аргументов по умолчанию x , y и z .

Лямбда с подписью signed ; без, без знака .

 q){[x;y](x*x)+(y*y)+2*x*y}[20;4] / лямбда со знаком
576
q){(x*x)+(y*y)+2*x*y}[20;4] / беззнаковая лямбда
576

Используйте x , y и z только в качестве имен первых трех аргументов

Использование других имен для первых аргументов лямбды часто помогает читателю. Но используя x , y или z для любого другого аргумента сеет путаницу.

Ранг

Ранг функции — это количество аргументов, которые она принимает.

Ранг подписанной лямбды — это количество имен в ее подписи.

Ранг лямбда-выражения без знака — это здесь самый высокий номер из трех имен аргументов по умолчанию x (1), y (2) и z (3), используемых в определении функции.

 {[h;l;o;c].5*(h-l;c-o)} / ранг 4
{x+y*10} / ранг 2
{x+z*10} / ранг 3

Результат

Результатом лямбда является результат последнего вычисленного оператора. Если последний оператор пуст, результатом является общий нуль, который не отображается.

 q)f:{2*x;} / последний оператор пуст
q)f 10 / результат не показан
q)(::)~f 10 / соответствует общему нулю
1б

Явный возврат

Чтобы успешно завершить вычисление и вернуть значение, используйте пустое присваивание, то есть : со значением справа и без переменной слева.

 с)с:0
д) е: {а: 6; б: 7;: а*б; с:: 98}
ф 0
42
р)с
0

Контроль оценки

Прервать

Чтобы немедленно прервать оценку, используйте сигнал, который равен ' со значением справа от него.

 с)с:0
q)g:{a:6;b:7;'`Конец;c::98}
д)г 0
{a:6;b:7;'`Конец;c::98}
'Конец
р)с
0

Обработка ошибок

Область имени

В контексте функции,

присвоение имен с : являются локальными для него и заканчиваются после оценки

Назначения
с :: являются глобальными (в корне сеанса) и сохраняются после оценки , если назначенное имя не является аргументом или уже определено как локальное

 q)a:b:0 / установить глобальные переменные a и b в 0
q)f:{a:10+3*x;b::100+a;} / f задает локальное a, глобальное b
q)f 1 2 3 / применить f
q)a / global a не изменяется
0
q)b / глобальный b обновляется
113 116 119
п)б:42
д){[а;б]б::99;a+b}[10;20] / присваивание является локальным
109
р)б
42
q){b:x=y;b::99;x+b}[10;20] / присваивание является локальным
109
р)б
42

Ссылки на имена , а не , назначенные локально, разрешаются в корне сеанса. Локальные назначения строго локальны : невидимы для других функций, применяемых во время оценки.

 q)a:42 / назначается в корне
д) е: {а + х}
q)f 1 / f читает a в корне
43
q){a:1000;f x}1 / f считывает a в корне
43

Локальные переменные идентифицируются при синтаксическом анализе и инициализируются как 9

В лямбда-выражениях прочитать и установить глобальные переменные с помощью получить и установить

получить , установить

Многострочное определение

В сценариях определения функций могут занимать несколько строк.

 sqsum:{[a;b] / квадрат суммы
  а2:а*а;
  б2:б*б;
  a2+b2+2*a*b / неявный результат
  }

Многострочные выражения

Переменные и константы

Определение лямбда может включать до:

	используется	текущий	V3.5
аргументы		8	8	8
местные жители	$м$	110	23	23
глобальные	$н$	110	31	31
константы		$239-(т+п)$	95	96

Ошибки синтаксического анализа

Лямбда-исчисление | Brilliant Math & Science Wiki

Содержание

Введение в лямбда-нотацию
Выражения
Свободные и связанные переменные
Скидки
Булевы значения
Церковные цифры
Упорядоченные пары
Реляционные операторы
Фиксированные точки и рекурсия 92\big) 7,(λx. x2)7, что на самом деле относится к 49.
Чтобы вычислить лямбда-выражение, нужно преобразовать его в каноническую форму, используя набор правил/сокращений преобразования, как мы увидим. Мы увидим, что λ\lambdaλ и .\bf{.}. (вместе с несколькими предопределенными переменными) сами по себе достаточно мощны, чтобы выразить любую вычислимую функцию.
Самая простая абстракция функции, которую я могу придумать и которая может быть выражена в лямбда-исчислении, — это тождественная функция: λx.x.\lambda x.x.λx.x.
Выражения можно рассматривать как программы на языке лямбда-исчисления.
Учитывая понятие переменной, обычно обозначаемое x,y,z,…,x,y,z,\ldots,x,y,z,…, мы определяем выражение индуктивно в терминах абстракций (анонимных функций) и приложения:
Пусть Λ\LambdaΛ — множество выражений.
Переменные: Если x\mathscr{x}x является переменной, то x∈Λ.\mathscr{x} \in \Lambda.x∈Λ.
Абстракции: Если x\mathscr{x}x является переменной и M∈Λ\mathscr{M} \in \LambdaM∈Λ, то (λx. M)∈Λ.(\lambda \mathscr{x}. \mathscr{M }) \in \Lambda.(λx.M)∈Λ.
Приложения: Если M∈Λ\mathscr{M} \in \LambdaM∈Λ и N∈Λ\mathscr{N} \in \LambdaN∈Λ, то (MN)∈Λ. \mathscr{N}) \in \Lambda. (MN)∈Λ.
Вот два важных соглашения:
Общее соглашение состоит в том, что применение функции является левоассоциативным, если в скобках не указано иное, т. е. E1E2E3≡((E1E2)E3). \mathscr{E}_1 \mathscr{E}_2 \mathscr{E}_3 \equiv \big((\mathscr{E}_1 \mathscr{E}_2) \mathscr{E}_3\big). E1E2E3≡((E1E2)E3).
Последовательные абстракции могут не содержать карри, т. е. λxyz.M≡λx.λy.λz.M. \lambda\mathscr{xyz}.\mathscr{M} \equiv \lambda\mathscr{x}. \лямбда\mathscr{y} . \лямбда\mathscr{z} . \mathscr{M}.λxyz.M≡λx.λy.λz.M.
Тело абстракции максимально расширяется вправо: λx.MN≡λx.(MN). \лямбда\mathscr{x}. \mathscr{MN} \equiv \lambda \mathscr{x}. (\mathscr{MN}). λx.MN≡λx.(MN).
В такой абстракции, как λx.x,\lambda x. x,λx.x, переменная xxx не имеет исходного значения, но является заполнителем. Мы говорим, что xxx является переменной связывает с λ.\lambda.λ.
С другой стороны, в λx.y\lambda x.yλx.y, т. е. в функции, которая всегда возвращает yyy, что бы ни потребовалось, yyy является свободной переменной, поскольку сама по себе имеет независимое значение.
Поскольку переменная привязана к некоторому подвыражению (область действия ), это не означает, что она связана везде. Например, это вполне правильное выражение (кстати, пример приложения): (λx.x)(λy.yx).(\lambda x.x) (\lambda y.yx).(λx.x) (λy.yx). Здесь xxx во вторых скобках не имеет ничего общего с xxx в первых.
Определим эти понятия формально:
x\mathscr{x}x свободен в выражении x\mathscr{x}x.
x\mathscr{x}x свободен в выражении λy.M\lambda \mathscr{y}.\mathscr{M}λy.M, если x≠y \mathscr{x} \neq \mathscr{y} x =y и x\mathscr{x}x свободен в M\mathscr{M}M.
x\mathscr{x}x свободен в MN\mathscr{M}\mathscr{N}MN, если x\mathscr{x}x свободен в M\mathscr{M}M или свободен в N\mathscr {Н} Н.
x\mathscr{x}x связан в выражении λx.M\lambda \mathscr{x}.\mathscr{M}λx.M.
x\mathscr{x}x связан в MN\mathscr{M}\mathscr{N}MN, если x\mathscr{x}x связан в M\mathscr{M}M или если он связан в N\mathscr {Н} Н.
Обратите внимание, что переменная может быть как связанной, так и свободной, но они представляют разные вещи, как мы обсуждали в примере выше.
Выражение без свободных переменных называется замкнутым выражением. (Сравните это с тем, как мы определяем предложения в логике предикатов.)
α\alphaα Эквивалентность:
Эквивалентность α\alphaα утверждает, что любая связанная переменная является заполнителем и может быть заменена ( переименована ) другой переменной при условии отсутствия конфликтов.
λx.x\лямбда х. xλx.x и λy.y\lambda y. yλy.y эквивалентны α\alphaα.
Однако это не всегда так просто. Рассмотрим выражение λx. (λx.x)\lambda x. (\lambda х. х) λx.(λx.x). Это α\alphaα эквивалентно λy.(λx.x)\lambda y. (\lambda x.x)λy.(λx.x), но не к λy.(λx.y)\lambda y. (\lambda х. у) λy.(λx.y). 9n_{j=m} f(j)∑i=mnf(i)=∑j=mnf(j). Это тоже самое.
(λy1.y1)(λx.(xx)) ( \lambda y_1 . y_1 ) \big( \lambda x . (x x) \big) (λy1.y1)(λx.(xx)) λy1.(λx.(xx)) \lambda y_1 . \big(\lambda x . (x x)\big) λy1.(λx.(xx)) λz.(λy.(z(+yz))) \lambda z . \Big( \lambda y . \big( z (+ y z) \big) \Big) λz.(λy.(z(+yz))) (λy1.y1)x(\lambda y_1 . y_1) x(λy1.y1)x
Какое из следующих выражений можно упростить до
(λx.x)x?(\lambda x.x)x?(λx.x)x?
Знаете ли вы, что такое исчисление λ\lambdaλ?
Давайте двигаться вперед и формализовать эту идею.
Для любого выражения M\mathscr{M}M и любого y\mathscr{y}y такого, что
х=у, х=у, х=у или
x\mathscr{x}x и y\mathscr{y}y не связаны в M,\mathscr{M},M, а y\mathscr{y}y несвободна в M,\mathscr{M}, М,
λx. M=αλy.(M{y/x}).\lambda \mathscr{x}. \mathscr{M} = _\alpha \lambda \mathscr{y} . \big( \mathscr{M} \left \{ \mathscr{y} /\mathscr{x} \right \} \big). λx.M=αλy.(M{y/x}).
Другими словами, все вхождения x\mathscr{x}x будут заменены на y\mathscr{y}y.
Если бы M{y/x} \mathscr{M} \left \{ \mathscr{y} /\mathscr{x} \right \} M{y/x} нужно было бы определить M{u/x} \mathscr{M} \left \{ u /\mathscr{x} \right \} M{u/x} для всех λ\lambda λ-функций u u u. Но замена всех вхождений x\mathscr{x}x на uuu не имеет смысла, так как λu.M{u/x} \lambda u. \mathscr{M} \left \{ u /\mathscr{x} \right \}λu.M{u/x} может быть не определено (в случае, если uuu не является переменной).
Следовательно, может возникнуть соблазн заменить все вхождения x\mathscr{x}x на uuu , кроме тех, которые следуют непосредственно за λ\lambdaλ
(\Big((т.е. (λx.M){u/x}= αλx.(M{u/x})).(\lambda x.\mathscr{M}) \left \{ u /\mathscr{x} \right \} =_\alpha \lambda x.\big(\ mathscr{M} \left \{ u /\mathscr{x} \right \}\big)\Big). (λx.M){u/x}=αλx.(M{u/x})) .
Но в этом случае, если u=y u = \mathscr{y} u=y, того факта, что y\mathscr{y}y не встречается в M\mathscr{M}M, уже недостаточно, как показано в следующем примере:
λx.(λx⋅x)⏟M{y/x}≠αλx.(λx⋅y)λx.(λx⋅y)⏟M{y/x}≠αλx.(λx⋅x). \lambda x.\underbrace{(\lambda x·x)}_{\mathscr{M}} \left \{ \mathscr{y} /\mathscr{x} \right \} \neq_\alpha \lambda x. (\лямбда х·у) \\ \lambda x.\underbrace{(\lambda x·y)}_{\mathscr{M}} \left \{ \mathscr{y} /\mathscr{x} \right \} \neq_\alpha \lambda x. (\лямбда х·х). λx.M(λx⋅x){y/x}=αλx.(λx⋅y)λx.M(λx⋅y){y/x}=αλx.( λx⋅x).
Вот почему мы должны убедиться, что
x=y, x=y, x=y или
x\mathscr{x}x и y\mathscr{y}y не связаны в M\mathscr{M}M, а y\mathscr{y}y не является свободным в M.\mathscr{M}.M.

β\betaβ редукция:
β\betaβ редукция является центральной идеей λ\lambdaλ исчисления. Он говорит нам, как работают упрощения абстракций.
Применим тождественную функцию (λx. 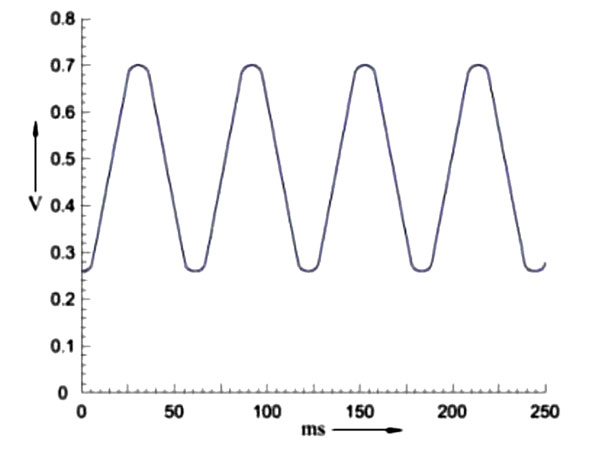{\ mathrm {\ beta}}} y. (λx.x)y⟶βy. 9{\ mathrm {\ beta}}} (\ lambda y .y ). (λx.x)(λy.y)⟶β(λy.y). Это просто, функция идентификации, примененная к функции идентификации, является самой функцией идентификации.
Здесь следует упомянуть важную особенность: β\betaβ-редукция не может привести к захвату свободной переменной другой абстракцией.
(λx.λy.(xy))(λx.λy.(xy)) \big(\lambda x . \lambda y . (x y)\big)\big(\lambda x . \lambda y . (x y)\ большой) (λx.λy.(xy))(λx.λy.(xy))
Наш первый шаг — подставить второе выражение как xxx в первое. Но делаем ли мы это так:
(λy((λx.λy.(xy))y))? \bigg( \lambda y \Big( \big(\lambda x . \lambda y . (x y)\big) y\Big) \bigg)? (λy((λx.λy.(xy))y))?
Нет! Потому что мы путаемся между исходными yyy и yyy второй абстракции. Если спуститься дальше по неправильному корню, получится следующее:
λy.λy.(yy). \лямбда у . \лямбда у . (г-г). λy.λy.(yy).
Это правильный путь:
(λx. {\mathrm{\beta}}} \lambda y’ . \лямбда у. (у’у). (λx.λy.(xy))(λx.λy.(xy))⟶βλy′.((λx.λy.(xy))y′)⟶βλy′.λy.(y′y).
ххх гггг λx.x\лямбда x.xλx.x Ничего из вышеперечисленного
Следующее выражение λ\lambdaλ можно упростить до какого из вариантов?
(λx.(λx.x))y(\lambda x.\big(\lambda x.x)\big)y(λx.(λx.x))y
Вдохновение: λ\lambdaλ исчисление
Пусть мы формализуем это с помощью понятия замены (избегающей захвата) свободных переменных.
Подстановка N\mathscr{N}N без захвата свободных вхождений x\mathscr{x}x в M\mathscr{M}M — M[N/x]\mathscr{M}[\mathscr{N }/\mathscr{x}]M[N/x] в символах — определяется следующим образом:
x[N/x]≡Ny[N/x]≡y(x≠y)(MP)[N/x]≡(M[N/x])(P[N/x])(λx.M )[N/x]≡(λx.M)(λy.M)[N/x]≡λy.(M[N/x])(x≠y,y не свободная переменная в N)(λy. M)[N/x]≡λy′.(M{y′/y}[N/x]). (x≠y,y – свободная переменная в N, y′ – новая переменная)\begin{aligned } \mathscr{x}[\mathscr{N}/x] &\equiv \mathscr{N} \\\\ \mathscr{y}[\mathscr{N}/x] &\equiv \mathscr{y} \qquad ( \mathscr{x} \neq \mathscr{y} ) \\\\ (\mathscr{MP}) [\mathscr{N}/\mathscr{x}] &\equiv \big(\mathscr{M}[\mathscr{N}/\mathscr{x}]\big)\big( \mathscr{P}[\mathscr{N}/\mathscr{x}]\big) \\\\ (\lambda \mathscr{x}. \mathscr{M})[\mathscr{N}/\mathscr{x}] &\equiv (\lambda \mathscr{x}. \mathscr{M}) \\\\ (\lambda \mathscr{y} . \mathscr{M})[\mathscr{N}/\mathscr{x}] &\equiv \lambda \mathscr{y} . \big(\mathscr{M}[\mathscr{N}/\mathscr{x}]\big) && ( \mathscr{x} \neq \mathscr{y} , \mathscr{y} \text{ не является свободная переменная в } \mathscr{N} ) \\\\ (\lambda \mathscr{y} . \mathscr{M})[\mathscr{N}/\mathscr{x}] &\equiv \lambda \mathscr{y’} . \Big(\mathscr{M}\left \{ \mathscr{y’}/\mathscr{y} \right \} [\mathscr{N}/\mathscr{x}]\Big). &&( \mathscr{x} \neq \mathscr{y} , \mathscr{y} \text{ свободная переменная в } \mathscr{N} , \mathscr{y’} \text{ свежая переменная}) \end{выровнено}x[N/x]y[N/x](MP)[N/x](λx. M)[N/x](λy.M)[N/x](λy.M) [N/x]≡N≡y(x=y)≡(M[N/x])(P[N/x])≡(λx.M)≡λy.(M[N/x] )≡λy′.(M{y′/y}[N/x]).(x=y,y не свободная переменная в N)(x=y,y является свободной переменной в N,y′ – свежая переменная) 9{\mathrm{\beta}}} \mathscr{M} [\mathscr{N} / \mathscr{x}] (λx.M)N⟶βM[N/x]
Два термина, которые могут быть сведены друг к другу нулевым или более β\betaβ-редукциями или обратными, являются β\betaβ-эквивалентными.

η\etaη Редукция:
Принцип экстенсиональности: две функции идентичны, если они делают одно и то же, т. е. одно и то же отображение.
Рассмотрим функцию λy.(xy)\lambda y. (xy)λy.(xy). Что произойдет, если мы применим это к произвольной переменной zzz?
Путем β\betaβ редукции получим xzx zxz. Разве это не то же самое, что применить xxx к z?z?z? Вместо применения λy.(xy)\lambda y. (x y)λy.(xy), мы могли бы также применить x.x.x.
Можно сказать, что xxx и λy.(xy)\lambda y. (x y)λy. {\mathrm{\eta}}} \mathscr{M}. λx.(Mx)⟶ηM.
хаскелл (\ х -> абс х)
лучше писать просто
Поскольку λ\lambdaλ-исчисление — это язык программирования, мы постепенно разработаем механизм для написания программ и кодирования структур данных на этом языке.
Для начала определим True как выбор первого элемента и False как выбор второго элемента :
T=λx.λy.xF=λx.λy.y.\begin{ выровнено} T &= \лямбда х . \лямбда у . Икс \\ F &= \лямбда х. \лямбда у. у. \end{выровнено} TF=λx.λy.x=λx.λy.y.
Но что это значит? Что ж, это не имеет значения, пока мы можем заставить их работать как булевы значения.
If-Then-Else
Вспомните обычные операторы if-then-else, используемые в функциональном или императивном программировании, или тернарный оператор в C++. В Haskell они имеют следующий вид:
Это означает, что мы выбираем это , если условие есть T,T,T, и если условие есть FFF, мы выбираем то . Это (не каламбур) подводит нас к следующей реализации if-then-else:if-then-else:if-then-else:
ifthenelse=λc.λx.λy.(cxy). ifthenelse = \lambda c . \лямбда х . \лямбда у . (с х у). ifthenelse=λc.λx.λy.(cxy).
Это работает благодаря тому, как мы определили TTT и FFF, то есть выбор первого и второго элемента соответственно.
Убедитесь, что
ifthenelse T a b=aifthenelse F a b= b.\begin{align} если иначе \, Т \, а \, b &= а \\ если иначе \, F \, a \, b &= \, b. \end{aligned}ifthenelseTabifthenelseFab=a=b.
Not
Теперь мы можем определить остальные логические элементы в терминах if-then-elseif-then-elseif-then-else. вместо может быть определено как , если True, то False, иначе True , что может быть записано как
not=λx.(x F T). не = \лямбда х. (х\,Ф\,Т). не=λx.(xFT).
И
и возвращает TTT, только если обе переменные имеют значение TTT. Таким образом, мы могли бы сказать, что если первый элемент равен FFF, результат определенно будет FFF, иначе результатом будет то, чем была вторая переменная. В Haskell
Или в исчислении λ\lambdaλ
and=λx.λy.(xyF). и = \лямбда х. \лямбда у. (x y F).and=λx.λy.(xyF).
Или
Точно так же мы могли бы представить
Или в исчислении λ\lambdaλ
или =λx.λy.(xTy). или = \лямбда х. \лямбда у. (x T y).or=λx.λy.(xTy).
Докажите, что λx.λy.(x(yFT)(yTF))\lambda x. \лямбда у. \big( x ( y F T) ( y T F) \big) λx.λy.(x(yFT)(yTF)) представляет исключающее или ( xor ) вентиль.
Можете ли вы реализовать другие логические элементы?
Любой полный по Тьюрингу язык должен уметь работать с некоторым представлением натуральных чисел. Это то, что делают церковные числительные в исчислении λ\lambdaλ. Эти цифры вдохновлены аксиомами Пеано.
Определим 0‾\overline{0}0 как λs.λz.z\lambda s . \лямбда г . zλs.λz.z, то же, что и FFF. Затем определим остальные церковные числительные как
1‾=λs.λz.s(z)2‾=λs.λz.s(s(z))3‾=λs.λz.s(s(s( z)))⋮\begin{выровнено} \overline{1} =& \lambda s . \лямбда г . с (г) \\ \overline{2} =& \lambda s . \лямбда г . с\большой(с(г)\большой) \\ \overline{3} =& \lambda s . \лямбда г . с \ большой (с \ большой (с (г) \ большой) \ большой) \\ &\vточки \end{aligned}1=2=3=λs.λz.s(z)λs.λz.s(s(z))λs.λz.s(s(s(z)))⋮ 9n(z)n=λs.λz.sn(z)
Преемник
Чтобы получить преемник n‾\overline{n}n, мы оборачиваем дополнительный sss вокруг числительного. Это не очень сложно:
S=λn.λs.λz.(s(nsz)).S = \lambda n. \лямбда с. \лямбда г. \big(s( n s z ) \big). S=λn.λs.λz.(s(nsz)).
Sn‾=n+1‾ S \overline{n} = \overline{n+1} Sn=n+1
У нас есть
Sn‾=λn.λs.λz.(s(nsz))n‾=(λn.λs.λz.s(nsz))(λs.λz.sn(z))=βλs′.λz′.s′ ((λs.λz.sn(z))s′z′)=βλs′.λz′.s′(s′n(z′))=λs′.λz′.s′n+1(z′) =αλs.λz.sn+1(z)=n+1‾. □\begin{выровнено} S \overline{n} &= \лямбда сущ. \лямбда с. \лямбда г. \big(s( n s z ) \big) \overline{n} \\ &= \big(\lambda n.\lambda s.\lambda z.s( n s z ) \big) \big(\lambda s . 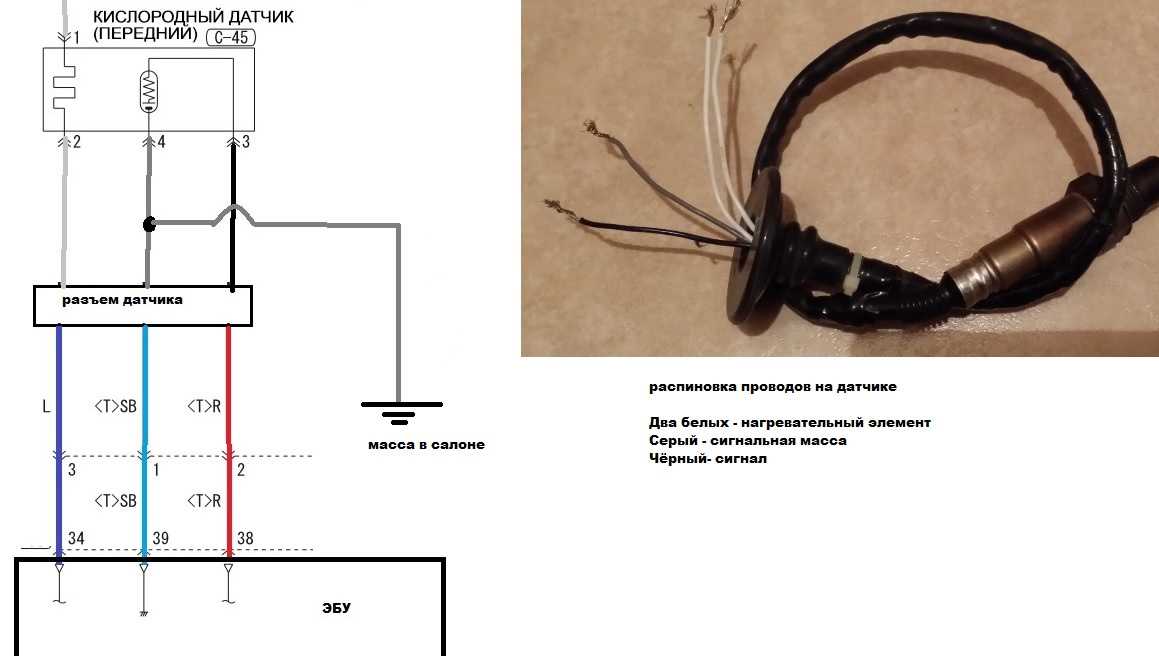{m+n}(z) && (\text{по определению} S) \\ &= \overline{m+n}.\ _\квадрат \end{aligned}addmn=(λmn.λsz.mSn)=(λs.λz.sm(z))S(λs.λz.sn(z))=βλz.Sm(z)(λs.λz .sn(z))=βSm(λs.λz.sn(z))=λsz.sm+n(z)=m+n. □(по определению S)
Умножение
Используя аналогичный аргумент, мы можем определить умножение следующим образом:
mult=λmn.m(add n)0‾.mult = \lambda mn . m (добавить \, n) \overline{0}. mult=λmn.m(addn)0.
Это просто, мы добавляем n‾\overline{n}n к 0‾\overline{0}0 ммм раз. Обратите внимание, что мы используем только один аргумент для addaddadd, когда говорим (add n)(add \, n)(addn). Это называется частичной заявкой .
Возведение в степень
Можете ли вы использовать приведенные выше идеи для реализации expexpexp таким образом, чтобы 9{\ overline {п}}? выражение = мн?
Предшественник
Задействована реализация функции предшественника. На самом деле, Черч долгое время думал, что это невозможно, пока его ученица Клини не нашла это. На самом деле, существует легенда, что Клини задумал эту идею во время посещения своего дантиста, поэтому трюк называется трюком с зубом мудрости .
Мы пропустим точную реализацию, пока не введем пары, но предположим, что это уже сделано, и назовем это предпредпред, так что
пред n‾=n−1‾.пред \, \overline{n} = \overline{n-1}. предn=n−1.
Вычитание
Вычитание можно реализовать так же, как сложение или умножение:
sub=λm.λn.n pred m. суб = \лямбда м . \лямбда сущ. п\, пред\, м. sub=λm.λn.nпредм.
Конечно, простейшим способом реализации упорядоченной пары (a,b)(a,b)(a,b) является абабаб, но он не позволяет получить два значения. Вместо этого мы реализуем такие пары:
. пара=λab.λz.zab пара = \lambda a b . \лямбда г. z a b пара=λab.λz.zab
То есть упорядоченная пара (a,b)(a,b)(a,b) равна (λz.ab)(\lambda z. a b)(λz.ab). Это полезно, потому что мы могли бы использовать TTT и FFF для извлечения первого и второго элементов соответственно (\big((называется левой проекцией (π1\pi_1π1) и правой проекцией (π2)):(\ pi_2)\big):(π2)):
π1=λp. pTπ2=λp.pF.\begin{выровнено} \pi_1 &= \лямбда стр. пТ \\\\ \pi_2 &= \лямбда с. пф. \end{выровнено}π1π2=λp.pT=λp.pF.
Почему это работает? Это из-за того, как мы определили TTT и F.F.F. 9{k+1} \big( пара \; \overline{0} \, \overline{0} \big) = \Phi \big(pair \; \overline{k} \, \overline{k-1}\ большой) = пара \; \overline{k+1} \, \overline{k}.Φk+1(pair00)=Φ(pairkk−1)=pairk+1k.
Следовательно, по индукции мы доказали наше утверждение. □_\квадрат□
Реализовать функцию предшественника теперь просто, достаточно выбрать второй элемент.
pred=λn.π2(nΦ(pair 0‾0‾))pred = \lambda n. \pi_2 \Big(n \Phi \big(pair \; \overline{0} \overline{0} \big) \Big) pred=λn.π2(nΦ(pair00))
Обратите внимание, что согласно этой реализации предшественником 0‾\overline{0}0 является сам 0‾\overline{0}0. Это будет полезно, как мы увидим в следующем разделе.
Действительно возможно кодировать связанные списки, отрицательные числа и/или рациональные числа в исчислении λ\lambdaλ. 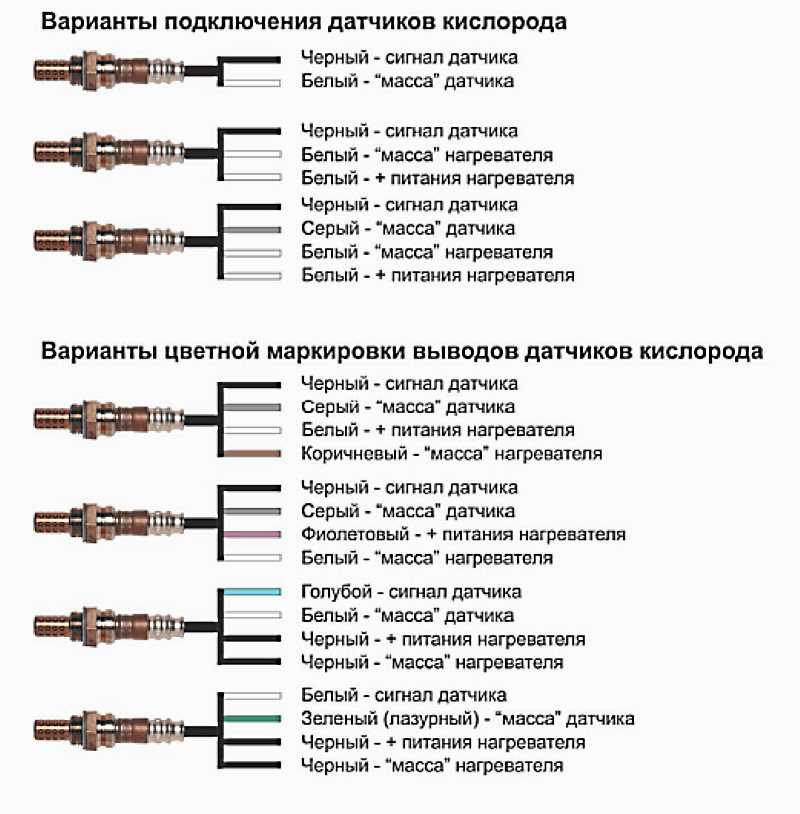Однако мы не обсуждаем это в этой вики.
Ноль?
Функция iszeroiszeroiszero возвращает TTT, если аргумент равен 000, и FFF, если это не так.
iszero=λn.n F not F iszero = \lambda n. n \, F \, не \, F равно нулю=λn.nFnotF
iszero n‾=Tif n=0=В противном случае.\begin{выровнено} iszero \, \overline{n} &= T && \text{if } n = 0 \\ &= F && \text{иначе}. \end{aligned} iszeron=T=Fif n=0иначе.
Напомним, что определения 0‾\overline{0}0 и FFF, которые мы использовали, эквивалентны α\alphaα.
Следовательно,
iszero 0=iszeroF=(λn.n F не F)F=βF F не F=не F=T.\begin{выровнено} iszero \, 0 &= iszero F \\ &= (\lambda н. п \, F \, не \, F) F \\ &=_\бета F \, F \, не \, F \\ &= не \, F \\ &= Т. \end{aligned}iszero0=iszeroF=(λn.nFnotF)F=βFFnotF=notF=T. 9п \, Ф \\ &= F.\ _\квадрат \end{выровнено} iszeron=(λn.nFnotF)n=nFnotF=Fn(not)F=(λxy.y)n(not)F=(λy.y)nF=F. □
Меньше
mmm меньше или равно nnn, если (sub m n)(sub \; m \, n)(submn) равно 0‾\overline{0}0. Это связано с тем, что предшественником 0‾\overline{0}0 по-прежнему является 0‾\overline{0}0, как мы отмечали в предыдущем разделе.
leq=λmn.isZero (sub m n) leq = \lambda mn. ноль \; (sub \; m \, n) leq=λmn.isZero(submn)
Равенство
Мы будем использовать свойство
(x≤y∧y≤x)→x=y. (x \leq y \клин y \leq x) \to x = y.(x≤y∧y≤x)→x=y.
eq=λmn.(и (leq m n) (leq n m)) eq = \lambda mn. \big(and \; (leq \; m \, n) \; (leq \; n \, m)\big) eq=λmn.(and(leqmn)(leqnm))
Как бы вы реализовали строгое «меньше» и «больше»?
Фиксированная точка xxx функции fff — это точка, которая отображается сама на себя, т. е.
f(x)=x.f(x) = x.f(x)=x.
потому что (х) = х
Точка, в которой сходится паутина, является фиксированной точкой функции косинуса. Значит, эта точка удовлетворяет уравнению
потому что⁡х=х. \cos х = х. косх=х.
Все действительные функции не обязательно имеют фиксированную точку. Однако в лямбда-исчислении все является функцией и также имеет неподвижную точку, что мы здесь и конструктивно докажем.
В исчислении λ\lambdaλ каждое выражение FFF имеет фиксированную точку.
Оказывается, существуют функции, называемые комбинаторами фиксированной точки , которые генерируют фиксированную точку для любого FFF.
Возьмем, к примеру, Парадоксальный комбинатор Карри или Y-комбинатор
Y=λf.(λx.f(xx))(λx.f(xx)). Y = \лямбда f. \big(\lambda x .f (x x)\big) \big(\lambda x .f (x x)\big). Y=λf.(λx.f(xx))(λx.f(xx)).
Мы утверждаем, что (YF)(Y F)(YF) является неподвижной точкой для любого FFF, т. е. F (Y F)=(Y F)F \, (Y \, F) = (Y \, F) F( ЙФ)=(ЮФ). Вот как:
YF=(λf.(λx.f(xx))(λx.f(xx)))F=β(λx.F(xx))(λx.F(xx))(1)=βF((( λx.F(xx))(λx. F(xx)))=F(YF). □(из (1)) \begin{aligned} Y F & = \Big( \lambda f. \big(\lambda x .f (x x)\big) \big(\lambda x .f (x x)\big) \Big) F \\ & =_\beta \big(\lambda x . F (x x)\big) \big(\lambda x . F (x x)\big) &&& (1) \\ & =_\бета F (\Big( \big(\lambda x . F (x x)\big) \big(\lambda x . F (x x)\big)\Big) \\ & = F(YF).\ _\квадрат &&& \big(\text{from} (1)\big) \end{выровнено} YF=(λf.(λx.f(xx))(λx.f(xx)))F=β(λx.F(xx))(λx.F(xx))=β F(((λx.F(xx))(λx.F(xx)))=F(YF). □(1)(из (1))
Существуют также другие комбинаторы с фиксированной точкой, такие как комбинатор Тьюринга
Θ=(λxy.y(xxy))(λxy.y(xxy)). \Theta = \big( \lambda xy . y (x x y) \big) \big( \lambda xy . y (x x y) \big). Θ=(λxy.y(xxy))(λxy.y(xxy)).
В качестве упражнения убедите себя, что Θ\ThetaΘ действительно является комбинатором с фиксированной точкой, написав доказательство.
Мы знаем, что в стандартной интерпретации натуральных чисел функция-преемник не имеет фиксированной точки. Однако в исчислении λ\lambdaλ это так. Какую интерпретацию мы можем дать этому?
Обратите внимание, что применение комбинатора YYY к SSS не дает числительного церкви ни в каком конечном числе редукций β\betaβ или η\etaη. Вместо этого мы получаем что-то вроде этого:
С(С(С(С…))). S\Big(S\big(S(S\ldots)\big)\Big). С(С(С(С…))).
Можно думать об этом как о неопределенном значении ⊥\bot⊥ или бесконечности, в любом из которых фиксированная точка понятна. □_\квадрат□
В Haskell fix from Control.Monad.Fix — это комбинатор с фиксированной точкой, реализованный следующим образом:
Рекурсия
Наше обсуждение комбинаторов с фиксированной точкой до этого момента было очень абстрактным. Как понимающий читатель, вы могли бы задаться вопросом, служат ли эти выражения какой-либо другой цели, кроме чистой математической красоты. На самом деле, они делают. Поскольку наши функции анонимны, мы не можем ссылаться на саму функцию внутри ее тела, используя ее имя. Для этого нам нужно решить функциональные «уравнения».
Рекурсия является центральной темой функционального программирования. Поскольку у нас нет циклов, мы используем рекурсию для нашего спасения.
Попробуем реализовать функцию, которая возвращает сумму первых nnn натуральных чисел, где nnn — аргумент.
Назовем эту функцию fff. Мы будем использовать рекурсию, чтобы сначала определить fff:
базовый случай: f 0‾=0‾ f \, \overline{0} = \overline{0} f0=0
формула рекурсии: f n‾=n‾+(f n−1‾)f \, \overline{n} = \overline{n} + \big(f \, \overline{n-1}\big ) fn=n+(fn−1)
С точки зрения идей, которые мы уже определили,
f n = ifthenelse (iszero n) 0‾ (добавить n (f (pred n))) ⇒f = λn.ifthenelse (iszero n) 0‾ (добавить n (f (pred n)). \ Begin {выровненные } f \, n &= ifThenElse \; (есть ноль \, п) \; \overline{0} \; \Big(добавить \, n \; \big(f \, (pred \, n) \big) \Big) \\ \Rightarrow f &= \lambda n. еслитоиначе \; (есть ноль \, п) \; \overline{0} \; \Big(добавить \, n \; \big(f \, (pred \, n) \big) \Big). \end{выровнено} fn⇒f=ifThenElse(isZeron)0(addn(f(predn)))=λn.ifThenElse(isZeron)0(addn(f(predn))).
Путем обратного бета-редукции в правой части мы получаем
f=(λg.λn.ifThenElse (isZero n) 0‾ (добавить n (g (пред n))))f. f = \bigg(\lambda g . \lambda n. ifThenElse \; (isZero \, n) \; \overline{0} \; \Big(add \, n \; \big(g \, (pred \, n) \big) \big) \bigg) f. f=(λg.λn.ifThenElse(isZeron)0(addn(g(predn))))f.
Это выглядит знакомо? Мы установили, что fff является неподвижной точкой (λg.λn.ifThenElse (isZero n) 0‾ (add n (g (pred n))))!\bigg(\lambda g . \lambda n. ifThenElse \; (isZero \, n) \; \overline{0} \; \Big(добавить \, n \; \big(g \, (pred \, n) \big) \Big) \bigg)!(λg.λn .ifThenElse(isZeron)0(addn(g(predn))))!
Следовательно, мы могли бы переписать уравнение следующим образом:
f=Θ(λg.λn.ifThenElse (isZero n) 0‾ (добавить n (g (pred n)))),f = \Theta \bigg(\lambda g . \lambda n. ifThenElse \; (isZero \ , n) \; \overline{0} \; \Big(добавить \, n \; \big(g \, (pred \, n) \big) \Big) \bigg), f=Θ(λg.λn .ifThenElse(isZeron)0(addn(g(predn)))),
, где Θ\ThetaΘ — комбинатор фиксированной точки Тьюринга. □_\квадрат□
Вот код Haskell для того же с некоторым синтаксическим сахаром:
Можете ли вы написать программу на λ\lambdaλ-исчислении для обозначения функции факториала?
Исчисление λ\lambdaλ является полным по Тьюрингу языком. Это означает, что универсальная машина Тьюринга (UTM) может быть эффективно смоделирована с использованием исчисления λ\lambdaλ и что UTM может оценивать функции, описанные исчислением λ\lambdaλ.
Функция f:N→Nf: \mathbb{N} \to \mathbb{N} f:N→N является вычислимой , если существует соответствующая лямбда-функция FFF такая, что Fn‾=f(n)‾ ∀ n∈NF \overline{n} = \overline{f(n)}\ \forall n \in \mathbb{N}Fn=f(n) ∀n∈N. Поскольку исчисление λ\lambdaλ эквивалентно по Тьюрингу, это то же определение вычислимости, что и в контексте машин Тьюринга. Согласно гипотезе Черча-Тьюринга, под это определение подпадает все, что вообще поддается физическому вычислению.
Одной из неразрешимых вещей в λ\lambdaλ-исчислении является эквивалентность двух лямбда-выражений. Это означает, что не существует алгоритма, который всегда может правильно предсказать, можно ли привести два заданных лямбда-выражения друг к другу. Это приложение теоремы Райса.
Еще одно примечательное неразрешимое свойство лямбда-выражений, тесно связанное с проблемой остановки, заключается в том, что не существует вычислимой функции, которая может сказать, имеет ли данное выражение нормальную форму.
Нормальная форма лямбда-функции является эквивалентной формой, в которой дальнейшие β\betaβ или η\etaη редукции невозможны. Например, λx.x\lambda x.xλx.x является нормальной формой, но Ω=(λx.(xx))((λx.(xx))\Omega = \big(\lambda x. (x x)\ big)\big((\lambda x. (x x)\big) Ω=(λx.(xx))((λx.(xx)) не имеет нормальной формы, так как приведение β\betaβ всегда приводит к выражению
В этой вики мы обсуждали только нетипизированный λ\lambdaλ исчисление.
Обратите внимание, что, хотя мы определяем логические значения, целые числа, функции для них и т. д., формального понятия недопустимости применения одного вида функции к другому не существует. В практическом программировании полезно различать типы, чтобы эффективно рассуждать о данных, с которыми мы работаем. Это также затрудняет для программиста написание программы на языке со статической типизацией.
Большое количество языков функционального программирования, включая Haskell, основано на идеях типизированного лямбда-исчисления и теории категорий.
Изоморфизм Карри-Ховарда-Ламбека представляет собой интересное математическое свойство, связывающее типизированное лямбда-исчисление или программирование в целом с логикой высказываний. В неформальной формулировке он говорит, что каждому соответствующему предложению соответствует соответствующий тип, который, если он обитаем (т. е. существует некоторая переменная этого типа), доказывает, что утверждение истинно, и, подобно каждому доказательству предложения, программа.
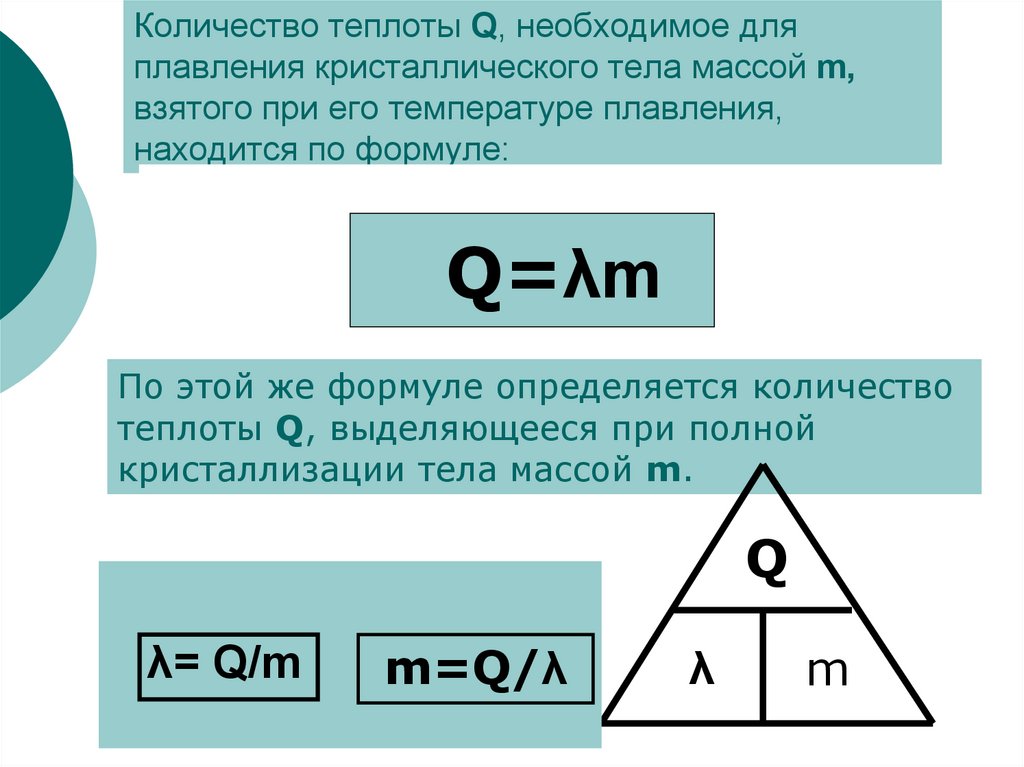
Цитировать как: Лямбда исчисление. Brilliant.org . Извлекаются из https://brilliant.org/wiki/lambda-calculus/
Измерение М-белка Тесты SPEP, UPEP
Эта важная группа анализов крови и мочи используется для оценки количества и активности миеломы. Эти тесты измеряют моноклональный белок, который клетки миеломы выделяют в кровь и/или мочу.
Электрофорез белков сыворотки и мочи (SPEP и UPEP)
Электрофорез белков сыворотки (SPEP) представляет собой тест, который измеряет количество моноклонального белка тяжелой цепи, вырабатываемого клетками миеломы. Подробнее читайте в разделе «Типы миеломы».
SPEP разделяет все белки в крови в соответствии с их электрическим зарядом. Электрофорез белков мочи, или UPEP, делает то же самое для белков в моче.
На первом графике представлен нормальный результат SPEP. Он показывает:
пик в измерении альбумина (наиболее распространенный белок в крови)
более низкие уровни других белков, сгруппированных в области, помеченные альфа 1 и 2
бета (с двумя выступами, также известными как 1 и 2)
гамма, где белки антител лежат на графике

Второй график представляет результат для пациента с миеломой. 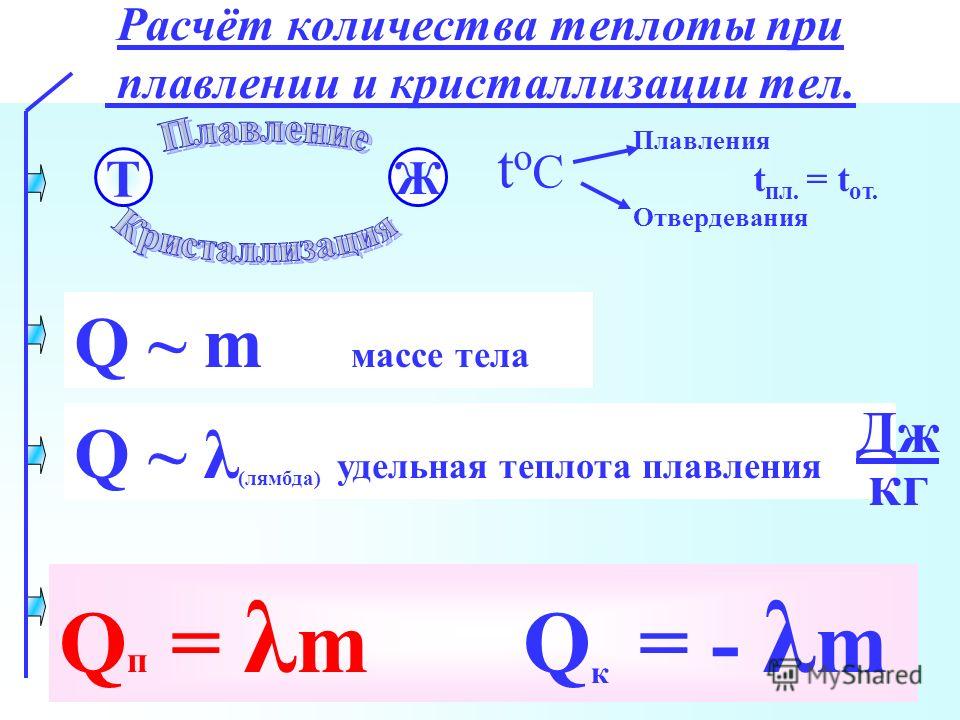Помимо всплеска альбумина, есть еще один высокий всплеск. Красная стрелка в гамма-диапазоне графика указывает на этот всплеск.
Патологоанатом измеряет площадь под шипом или кривой и вычитает нормальный уровень гамма-глобулинов из общего количества. Результатом является ваш уровень моноклонального белка (М-белка).
SPEP и UPEP говорят нам, сколько существует моноклонального белка, но не его тип. Моноклональный белок является продуктом миеломных клеток у большинства людей с миеломой. Тем не менее, миелома у каждого человека уникальна. Выход моноклонального белка может варьироваться от пациента к пациенту. Это также может варьироваться в зависимости от того, как это количество связано с поведением миеломы.
SPEP и UPEP не измеряют клетки миеломы; они измеряют выход клеток миеломы. Клетки миеломы человека не размножаются с одинаковой скоростью и не выделяют одинаковое количество белка на клетку.
Предостережение относительно SPEP: моноклональный белок иммуноглобулина А-типа (IgA) миеломы не выделяется в гамма-области графика. Он может «застрять» с бета- или даже альфа-белками. Пациенты с миеломой IgA должны обсудить лучший способ измерения моноклонального белка со своим врачом.
Иммунофиксационный электрофорез крови или мочи (ИФЭ)
Иммунофиксационный электрофорез крови или мочи (ИФЭ) является аналогом SPEP и UPEP. IFE сообщает нам ТИП моноклонального белка в крови и/или моче, но не его количество. Тестирование IFE разделяет белки по электрическому заряду. IFE измеряет только моноклональные или аномальные белки, но не нормальные (поликлональные)
Положительный или отрицательный результат на присутствие определенного типа моноклонального белка.
*Примечание: Дарзалекс может повлиять на результаты IFE, если у пациента есть IgG-каппа-миелома и его оценивают на предмет полного ответа. У пациента может быть очень глубокий полный ответ, но в тесте будет обнаружена крошечная полоска IgG каппа.
Количественное тестирование на иммуноглобулины или QIg
Количественное тестирование на иммуноглобулины часто проводится как часть раннего скрининга на ММ. Обычно это делается, если уровень общего белка повышен. QIg измеряет общий белок иммуноглобулина в крови, как в норме, так и в норме. Если QIg обнаруживает повышение уровня иммуноглобулина, необходимо пройти дополнительное тестирование с помощью ИФЭ. Цель состоит в том, чтобы увидеть, связано ли это увеличение с аномальным (моноклональным) белком.
Некоторые врачи также используют QIg для наблюдения за пациентами с миеломой IgA, потому что IgA трудно оценить с помощью SPEP.

Бессывороточный анализ легких цепей или тестирование Freelite®

Бессывороточный анализ легких цепей (торговая марка Freelite®) используется для диагностики и мониторинга миеломы. Белки иммуноглобулинов состоят из двух типов молекул: тяжелых цепей и легких цепей (см. схему).
Эти тяжелые и легкие цепи обычно связаны вместе как «цельные иммуноглобулины». По неизвестным нам причинам плазматические клетки производят больше легких цепей, чем тяжелых цепей. Избыток или несвязанные легкие цепи свободно циркулируют в крови. Поэтому их называют «свободными» легкими цепями. Эти свободные легкие цепи присутствуют как у здоровых людей, так и у пациентов с миеломой и родственными заболеваниями. Связанные расстройства включают:
МГУС
СММ
амилоидоз
Болезнь отложения легких цепей (LCDD)
Макроглобулинемия Вальденстрема
Пациенты с миеломой могут узнать, что их клетки секретируют:
как тяжелые, так и легкие цепи
только тяжелые цепи
только легкие цепи
У некоторых пациентов при оценке с помощью SPEP вообще не секретируется М-белок. Клетки миеломы этих пациентов не секретируют белок тяжелой цепи, а только очень небольшое количество белка легкой цепи. Тест Freelite используется для пациентов, которым
секретируют только легкие цепи, что часто называют «миеломой Бенс-Джонса».
секретируют как тяжелые, так и легкие цепи
выделяют очень низкий уровень белка, также известный как «олигосекреторная миелома»
Анализ Freelite также используется для:
диагностики и наблюдения за пациентами с MGUS, нераковым повышением уровня моноклонального белка.