Радиус скругления дорог: ГОСТ Р 58653-2019 Дороги автомобильные общего пользования. Пересечения и примыкания. Технические требования / 58653 2019

Содержание

Что такое радиус разворота, каким он бывает, и почему он важен?

  • Главная
  • Статьи
  • Что такое радиус разворота, каким он бывает, и почему он важен?

Автор: Алексей Кокорин

При выборе автомобиля обычно смотрят на его ключевые характеристики: размер, объем и мощность двигателя, тип трансмиссии и так далее. Однако в повседневной жизни есть и другие показатели, которые оказываются весьма важными – к примеру, радиус разворота. На что влияет это значение, как его замеряют, и почему важно не запутаться в этом, казалось бы, элементарном понятии?

 

Что такое радиус разворота?

Как нетрудно догадаться, радиус разворота – это радиус полуокружности, которую описывает автомобиль при развороте с места на 180 градусов при условии, что руль повернут до упора.

Правда, как мы убедимся чуть ниже, само словосочетание «радиус разворота» весьма коварное.

На что влияет радиус разворота?

Радиус разворота – показатель, во многом отражающий маневренность автомобиля. Чем он больше, тем больше места требуется автомобилю для совершения полного разворота на 180 градусов – то есть, в условиях, когда ширина дороги известна и ограничена, этот показатель отражает то, сможете ли вы развернуться на ней в один прием, или же придется сдавать назад и быстро крутить рулем на втором (а то и третьем) заходе. Однако очевидно, что сам по себе радиус разворота говорит не только о способности развернуться, но и о том, насколько маневренным является автомобиль: чем меньше это значение, тем удобнее будет управлять машиной в стесненных условиях и легче парковаться.

Как замеряется радиус разворота?

Даже для замера этого элементарного на первый взгляд показателя существует две методики: «от бордюра до бордюра» и «от стены до стены».

Первый отражает радиус полуокружности, которую описывают колеса автомобиля при развороте: то есть, чтобы его замерить, нужно отметить мелом стартовое положение наружного (относительно поворота) колеса, затем вывернуть руль до упора, развернуться на 180 градусов, отметить мелом конечную точку, замерить расстояние между ними и разделить его пополам. Соответственно, эта методика замера отражает, какой должна быть ширина гладкой дороги, чтобы автомобиль смог развернуться, не съехав с нее.

Однако в реальной жизни стоит учитывать тот факт, что у автомобиля есть передний свес – то есть, расстояние от оси передних колес до конца переднего бампера. И если дорога, к примеру, ограничена высокими бордюрами, то развернуться на ней, даже «укладываясь» по показателю от бордюра до бордюра, не выйдет: автомобиль упрется в препятствие выступающим вперед бампером. Для отражения этого «реального» радиуса разворота используют показатель «от стены до стены»: соответственно, чтобы замерить его, нужно закрепить мел на стержне, установленном на наружном (относительно поворота) углу бампера автомобиля, затем выполнить разворот, замерить диаметр получившейся полуокружности и разделить его пополам.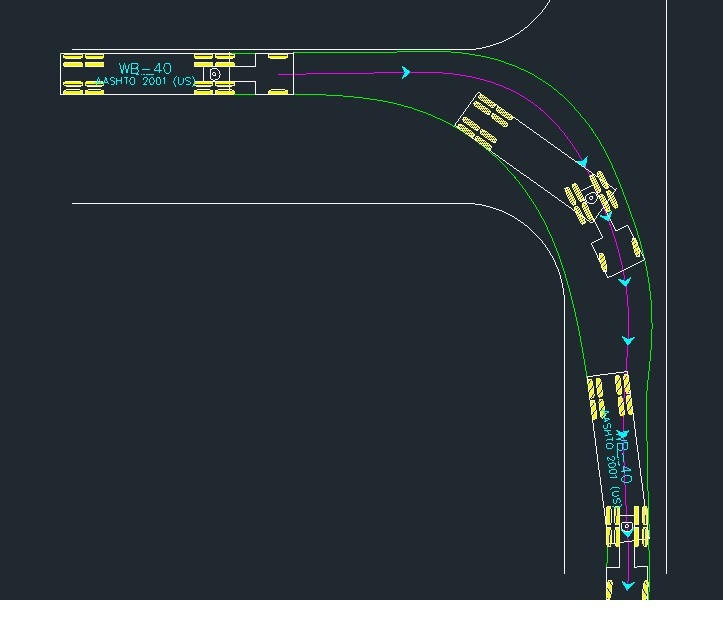

Разумеется, автопроизводители стремятся показать свои автомобили максимально маневренными, так что в брошюрах и списках характеристик практически всегда указывается радиус разворота от бордюра до бордюра, так как он меньше, чем от стены до стены. В реальной жизни, сравнивая машины по показателю маневренности, стоит учитывать не только на эту цифру, но и длину переднего свеса.

В чем часто ошибаются при указании радиуса разворота?

Главная проблема, связанная с радиусом разворота, заключается в том, что само словосочетание «радиус разворота» является скорее разговорным, ведь реальный показатель, отражающий расстояние, необходимое для разворота «от упора до упора» – это диаметр. Соответственно, при перечислении габаритных и технических характеристик автомобиля зачастую указывают именно его, хотя можно встретить и радиус. Но главное при этом – не перепутать эти два показателя. Ведь даже сами производители порой ошибаются: к примеру, в пресс-релизе о новом Land Cruiser Prado в Toyota говорят о том, что он «сохранил удобный

диаметр разворота, составляющий всего 5,8 м», что для машины длиной в 4,84 метра выглядит явно невозможным. А вот в брошюре по модели указано, что это «минимальный радиус разворота по колесам», что уже похоже на правду. Чтобы в этом убедиться, можно заглянуть, к примеру, на австралийский официальный сайт, где указан уже не радиус, а
диаметр разворота, равный 11,6 метра.

Можно ли изменить радиус разворота автомобиля?

Несложно догадаться, что радиус разворота зависит прежде всего от габаритных размеров автомобиля и угла поворота передних колес. Габариты машины поменять, очевидно, нельзя, а угол поворота колес на гражданских автомобилях ограничен параметрами работы рулевого управления, а на машинах с приводом на переднюю ось еще и рабочими диапазонами шарниров равных угловых скоростей (ШРУС, или «гранат»), которые крайне не любят работать при вывернутых колесах. Поэтому, не углубляясь в теорию, можно ответить так: без вмешательства в конструкцию с потерей гарантии нормальной работоспособности изменить радиус разворота машины нельзя.

Наглядным примером «вмешательства в конструкцию» можно считать автомобили, подготовленные для соревнований по дрифту: у них угол поворота передних колес («выворот») стараются сделать максимальным. Но нужно это уже не для уменьшения радиуса разворота, а для того, чтобы поддерживать как можно больший угол заноса при движении в повороте – то есть, это делается отнюдь не для улучшения показателей «гражданской» эксплуатации.

популярные вопросы

 

Новые статьи

Статьи / Интересно Долгожданное прощание: почему погибла Lada Xray, но об этом никто не пожалел На прошлой неделе мы официально попрощались с Lada Xray: президент АВТОВАЗа Максим Соколов заявил, что модель никогда не вернется на конвейер. Это угадывалось еще весной, когда вслед за ост… 1649 2 1 16.

09.2022

Статьи / Ралли Мой финиш – горизонт: как мы участвовали в гонке «Сила Сибири» Недавно мы рассказывали о том, как прокатились на Jeep Wrangler из Москвы в Томск, чтобы принять участие во внедорожном турнире «Сила Сибири». Разумеется, бороться за первое место мы планир… 277 0 1 16.09.2022

Статьи / Дилер Россия без Renault: как выживают дилеры и автовладельцы после ухода компании С момента, когда компания Renault объявила об уходе из России, прошло ровно четыре месяца. За это время многое стало понятно: доля французов в АВТОВАЗе ушла государству, завод в Москве переш… 2893 4 4 15.

09.2022

Популярные тест-драйвы

Тест-драйвы / Тест-драйв Полный привод, самый мощный мотор и силы в запасе: первый тест Chery Tiggo 8 PRO MAX Появление в российской линейке Chery модели Tiggo 8 PRO MAX можно назвать знаковым для бренда. Почему? Да хотя бы потому, что это первый с 2014 года полноприводный кроссовер Chery, приехавши… 17938 13 44 29.04.2022

Тест-драйвы / Тест-драйв Мотор от Mercedes, эмблема от Renault, сборка от Dacia: тест-драйв европейского Logan 1,0 Казалось бы, что нового можно рассказать про Renault Logan второго поколения, известный каждому российскому таксисту, что называется, вдоль и поперёк? Однако конкретно в этом автомобиле есть.

.. 9597 10 41 13.08.2022

Тест-драйвы / Тест-драйв Haval Dargo против Mitsubishi Outlander: собака лает, чужестранец идет В дилерском центре Haval на юге Москвы жизнь кипит: покупатели разглядывают машины, общаются с менеджерами и подписывают какие-то бумаги. Пока я ждал выдачи тестового Dargo, такой же кроссов… 8644 3 36 13.09.2022

схема, разворот еврофуры в метрах и на 90 градусов

Во время движения большегрузных автомобилей, особенно фур с прицепом, у которых линейные размеры 20 м и больше, происходят другие физические процессы при выполнении поворота, чем у легкового транспорта или автобусов. В специальной литературе эти технологические движения описаны тщательно, приведены схемы и рисунки. Некоторые нюансы постараемся доходчиво объяснить читателям в этой статье.

Содержание

  1. Что такое радиус поворота
  2. Особенности маневрирования
  3. Радиус разворота еврофуры
  4. Радиус поворота «американца»
  5. Расчет радиуса по лекалам
  6. Прохождение поворотов
  7. Советы дальнобойщику

Что такое радиус поворота

Многие автолюбители «не в теме», и редко кто из них знает, что такое радиус поворота фуры. Согласно специальной технической литературе – это воображаемая дуга, по линии которой перемещается центр тяжести тягача с полуприцепом при выполнении сложного маневрирования. Максимальное значение этой величины (радиуса) во многом зависит от специфической конструкции транспортного средства.

При движении по шоссе каждый водитель должен быть в курсе специфических нюансов при съезде фур на развязку или на перекрестках, чтобы случайно не получить боковой удар кормой полуприцепа.

Вот как фура во время поворота может зацепить своим полуприцепом легковой автомобиль:

Есть специальный термин – расчетный автомобиль, его тактико-технические показатели используются при разработке проектов трасс регионального значения. Такие параметры, например: размер и R min поворота должны быть идентичными у каждого класса автотранспорта.

Нормы европейского стандарта регламентируют следующие габариты для автотранспорта большегрузной категории во время движения на поворотах:

  • при R наружном в 12,5 м – R внутренний будет равен или меньше 5,3 м;
  • коридор для вписывания в поворот – 7,2 м;
  • R min наружный не должен превышать 12,5 м.

Например: для автопоезда типа А16, имеющего линейный размер до 16 метров, и аналогичного вида А20 с длиной до 20 м прописаны строгие ограничения, указанные в приведенной ниже таблице:

Тип автомобиляR min поворота, мR min внешний, мR min внутренний, м
А169,710,26,2
А2012,112,68,5

Типичными прототипами для расчетных автомобилей могут служить:

  • автопоезд до 16 м – MAN F-200019.403 FLT или европейская фура с габаритами 16,5 × 2,5 м, где первый параметр – линейный, а второй – ширина;
  • 20-метровый вариант – «Мерседес-Бенц Актрос» или СЗАП-8357А, с габаритами 19,8 на 2,5 м.

Автопоезда с двумя или тремя прицепами, имеющие длину больше 20 метров, используются всеми перевозчиками мира, поэтому при разработке макетов автотрасс нужно проводить дополнительное компьютерное моделирование такого специфического движения во время поворотов на пересечениях дорог или городских перекрестках.

Автопоезд на дороге

Особенности маневрирования

Водители-дальнобойщики обладают специфической подготовкой: уверенно входят в повороты на трассе и во время перемещений по городу, при прохождении перекрестков, потому что движения отработаны до автоматизма на специальных дорожках автодрома, как показано на этом видео:

Такой термин, как радиус разворота фуры должен учитываться при разработке подъездных путей к складским помещениям и местам разгрузки крупнотоннажного автомобильного транспорта. А разворотная площадка для фуры должна соответствовать утвержденным стандартам, чтобы большегрузный автомобиль мог уверенно маневрировать на выделенной для этих целей территории.

Таблица ширины площадки для ТС (транспортных средств)

Тип автоДлина ТС в мШирина площадки, м
Камаз1022
Еврофура1838

Для нормального выполнения маневрирования при движении ТС надо располагать на площадке разгрузки друг от друга на расстоянии 3–4 метра.

Радиус разворота еврофуры

Европейские стандарты регламентируют ограничения по длине, например, для седельного автопоезда этот параметр – 16,5 метра. Размеры полуприцепа: 12 м от оси ССУ до кормовой части и 2,1 м до переднего бампера.

Стандартный радиус разворота еврофуры, например, на 180 или 360 градусов внутри воображаемой площади, которая составлена двумя окружностями с R = 12,5 м и 5,3 м, должен свободно выполняться при условии, что выступающие части машины не пересекают обозначенные границы во время маневрирования.

Схематическое изображение радиуса разворота фуры

Радиус поворота «американца»

Тягачи с полуприцепами, разработанные американскими конструкторами, называют траками, а маневренность, особенно во время проезда по городу, ограниченная из-за большого линейного размера. Для поворота на 90 градусов такому крупногабаритному транспортному средству требуется в 2 раза больше радиуса, чем европейским аналогам. Поэтому иногда приходится видеть такие ситуации, как на фото.

Неправильный разворот фуры

В городской черте такие автомобили не могут осуществлять безаварийное движение, чтобы постоянно не нарушать ПДД, затрудняют перемещение другого автотранспорта, т. к. их длина не соответствует европейским стандартам. Владельцы легковых автомобилей вынуждены держаться на расстоянии от «американцев», чтобы не попасть под удар разворачивающегося «монстра».

Расчет радиуса по лекалам

При строительстве дорог во время осуществления проекта в компьютерном варианте используют специальные лекала, по которым скрупулезно выписывается кривизна каждого изгиба, особенно на развязке и пересечении с другими аналогами.

Как правило, лекала уже рассчитаны для всех типов автотранспортных средств. Такие данные можно скачать, например, по этой ссылке – https://dwg.ru/dnl/2627.

Прохождение поворотов

Умудренные опытом дальнобойщики чувствуют габариты автотранспортного средства, состоящего из тягача и полуприцепа с неуправляемой тележкой, а также возникающие сложности, связанные со смещением последней при вхождении в поворот.

Изящное прохождение перекрестка

Гораздо больше внимания водителю фуры требуется при выполнении маневрирования в черте города, где интенсивное движение пешеходов, а также легкового и общественного транспорта. Особо надо отметить сложности при проезде развязок и перекрестков – все необходимые маневры по изменению направления и смены полосы движения нужно выполнить заранее, но не ближе, чем за 20 метров от начала развязки или пересечения дорог.

Выполняя поворот направо, следует обратить внимание на встречную полосу дороги, т. к. автопоезд часто выезжает на нее, чтобы избежать заезда колесами тележки полуприцепа на бордюр, создавая угрозу травматизма пешеходов. При левом повороте не нужно стремиться проезжать центр перекрестка, потому что увеличивается площадь разворота, что затрудняет другому транспорту движение в нужную сторону.

Погрешности в повороте

Советы дальнобойщику

Управлять фурой так же трудно, как водить корабль по морю, здесь нужны навыки, многолетний опыт и профессионализм:

  • Никаких резких движений – сзади груз, который превосходит массу тягача. Его инерция толкает машину вперед, и это нужно постоянно помнить, потому что резко изменить направление проблематично.
  • Опасный момент вождения – это повороты, т. к. ведомая конструкция стремится по инерции вперед, что чревато складыванием пополам. Не стоит делать резких движений, а только плавно управлять техникой и не «газовать».
  • Когда выпадают осадки, то такие физические законы, как трение – не действуют, поэтому нужно правильно выбрать скорость пропорционально качеству дорожного полотна.
  • При поворотах на перекрестках помните, что водители соседних машин начинают движение раньше, чем задняя часть автопоезда проедет мимо. Не ленитесь посмотреть в зеркала, чтобы исключить столкновение.
  • Помните, что лихачи совершают рискованные обгоны, занимая освободившееся место между двигающимся транспортом. В случае экстренной ситуации нарушители успеют затормозить, а у вас сзади груз, так что мгновенно остановиться не получится.
  • Следует постоянно помнить, что у полуприцепа самостоятельная траектория движения, поэтому выбирайте радиус немногим больше, чтобы исключить выезд его за линию дороги.
  • Не стоит обгонять, когда не просматривается впереди лежащая дорога, резко свернуть или затормозить уже не получится.

Важно! Сложным маневром считается постановка фуры на разгрузку. Не забывайте – полуприцепом руководят задние, а не передние колеса. Постоянно совершенствуйте профессиональные навыки, выполняя тренировочное маневрирование на специальных площадках.

Надеемся, что приведенные в статье рекомендации по прохождению сложных участков дороги помогут дальнобойщикам избежать нарушений ПДД. Помните, что опытный шофер видит далеко, а профессионал уверенно контролирует ситуацию вокруг управляемого транспортного средства.

Радиус разворота легкового автомобиля таблица

Что такое радиус разворота

Уже из названия характеристики можно догадаться о её сути. Под этим параметром подразумевается полуокружность, которую описывает автомобиль во время манёвра при полностью вывернутом рулевом управлении. Знать это значение нужно обязательно. Более того, необходимо отличать разворот по малому и большому радиусу.

Схематичное изображение поворота авто

Некоторые производители указывают в качестве радиуса разворота два параметра, разделённых между собой дробью. Минимальный показатель поворота автомобиля соответствует следу от наружного колеса, который оставляет транспортное средство при манёвре. Такой показатель называется «от бордюра до бордюра». Это значение не учитывает размеры переднего свеса, от длины которого зависит точность показателя.

На практике удобнее использовать другое значение — радиус «от стены до стены». В этом случае учитываются препятствия, которые входят в минимальное пространство по наружным габаритам и могут быть задеты бампером. Но и на этом ещё не всё. Существует ещё один нюанс, который нужно учитывать водителю при езде в ограниченном пространстве.

Значение для авто с прицепом

При повороте некоторая часть кузова смещается во внутреннюю сторону. Потому при выезде со стоянки нельзя резко выворачивать руль до предельного положения. При таких действиях можно задеть соседний автомобиль. Чтобы понять какой радиус нужен для разворота, необходимо определить минимальный габаритный коридор для своей машины. Для этого нужно знать расстояние, которое отделяет максимальную и минимальную окружности.

Такая осведомлённость позволит не только без проблем маневрировать в сложных условиях и делать правильные манёвры на узкой дороге, но и выполнять поворот на дороге согласно разъяснениям ГИБДД 2020 года.

Насколько важен параметр

Современным водителям приходится ездить в непростых условиях: машин много, а места для них часто не хватает. Особенно это касается парковочных мест в больших городах и людных местах. Часто водителю приходится втискиваться между машинами впритык и выполнять сложные манёвры среди других автомобилей.

Радиус поворота отображает маневренность автомобиля, его способность выполнять повороты на узкой дороге и в ограниченном пространстве. Чем меньшим является этот параметр, тем более комфортным и простым будет управление ТС во время передвижения в ограниченном пространстве. Если известен радиус разворота и ширина дороги, то можно путём проведения несложных расчётов узнать вероятность осуществления манёвра за один раз.

Производители автомобилей обязательно указывают интересующее нас значение для каждого автомобиля. Этот показатель можно найти в практическом руководстве или техническом описании. Но здесь может ждать подвох. Многие производители указывают минимальный показатель — разворот по малому радиусу. Это позволят им представить своё творение более маневренным, чем есть на самом деле. Чтобы узнать действительный показатель, необходимо учитывать размеры свеса автомобиля.

Сравнение показателей маневренности с разными прицепами и без них

Как измеряем

Мы уже говорили выше о двух значениях, которые отображают радиус поворота автомобиля. Для вычисления каждого из них используются разные методы.

  1. Для вычисления параметра «от бордюра до бордюра» необходимо при помощи мела сделать отметку начального положения наружного колеса. Выворачиваем руль пока он не примет граничное положение, разворачиваем автомобиль на 180 градусов. Отмечаем конечное положение колеса. Между полученными отметками измеряем расстояние. Половина от этого результата будет отражать искомое значение. Он будет обозначать необходимую ширину дороги, которая потребуется для разворота авто.
  2. Более реальное значение отображает характеристика «от стены до стены». Для её вычисления потребуется зафиксировать стержень на наружном углу бампера. На стержне крепится мел и выполняется разворот машины, как это делалось в предыдущем случае. Получится полуокружность, в которой потребуется измерить диаметр. Половина этого значения будет отражать нужный нам радиус разворота машины.

В свободном доступе имеются таблицы с радиусом разворота легкового автомобиля. Также найти нужный показатель для конкретной марки машины можно в руководстве по эксплуатации и техническом описании

В любом случае, на этот параметр нужно обращать внимание. Эти знания позволят избежать неприятных ситуаций на дороге и паркинге

Лучшие цены и условия на покупку новых авто

Советы дальнобойщику

Управлять фурой так же трудно, как водить корабль по морю, здесь нужны навыки, многолетний опыт и профессионализм:

  • Никаких резких движений – сзади груз, который превосходит массу тягача. Его инерция толкает машину вперед, и это нужно постоянно помнить, потому что резко изменить направление проблематично.
  • Опасный момент вождения – это повороты, т. к. ведомая конструкция стремится по инерции вперед, что чревато складыванием пополам. Не стоит делать резких движений, а только плавно управлять техникой и не «газовать».
  • Когда выпадают осадки, то такие физические законы, как трение – не действуют, поэтому нужно правильно выбрать скорость пропорционально качеству дорожного полотна.
  • При поворотах на перекрестках помните, что водители соседних машин начинают движение раньше, чем задняя часть автопоезда проедет мимо. Не ленитесь посмотреть в зеркала, чтобы исключить столкновение.
  • Помните, что лихачи совершают рискованные обгоны, занимая освободившееся место между двигающимся транспортом. В случае экстренной ситуации нарушители успеют затормозить, а у вас сзади груз, так что мгновенно остановиться не получится.
  • Следует постоянно помнить, что у полуприцепа самостоятельная траектория движения, поэтому выбирайте радиус немногим больше, чтобы исключить выезд его за линию дороги.
  • Не стоит обгонять, когда не просматривается впереди лежащая дорога, резко свернуть или затормозить уже не получится.

Надеемся, что приведенные в статье рекомендации по прохождению сложных участков дороги помогут дальнобойщикам избежать нарушений ПДД. Помните, что опытный шофер видит далеко, а профессионал уверенно контролирует ситуацию вокруг управляемого транспортного средства.

Особенности маневрирования

Водители-дальнобойщики обладают специфической подготовкой: уверенно входят в повороты на трассе и во время перемещений по городу, при прохождении перекрестков, потому что движения отработаны до автоматизма на специальных дорожках автодрома, как показано на этом видео:

Такой термин, как радиус разворота фуры должен учитываться при разработке подъездных путей к складским помещениям и местам разгрузки крупнотоннажного автомобильного транспорта. А разворотная площадка для фуры должна соответствовать утвержденным стандартам, чтобы большегрузный автомобиль мог уверенно маневрировать на выделенной для этих целей территории.

Таблица ширины площадки для ТС (транспортных средств)

Тип автоДлина ТС в мШирина площадки, м
Камаз1022
Еврофура1838

Радиус разворота еврофуры

Европейские стандарты регламентируют ограничения по длине, например, для седельного автопоезда этот параметр – 16,5 метра. Размеры полуприцепа: 12 м от оси ССУ до кормовой части и 2,1 м до переднего бампера.

Стандартный радиус разворота еврофуры, например, на 180 или 360 градусов внутри воображаемой площади, которая составлена двумя окружностями с R = 12,5 м и 5,3 м, должен свободно выполняться при условии, что выступающие части машины не пересекают обозначенные границы во время маневрирования.

Схематическое изображение радиуса разворота фуры

Радиус поворота «американца»

Тягачи с полуприцепами, разработанные американскими конструкторами, называют траками, а маневренность, особенно во время проезда по городу, ограниченная из-за большого линейного размера.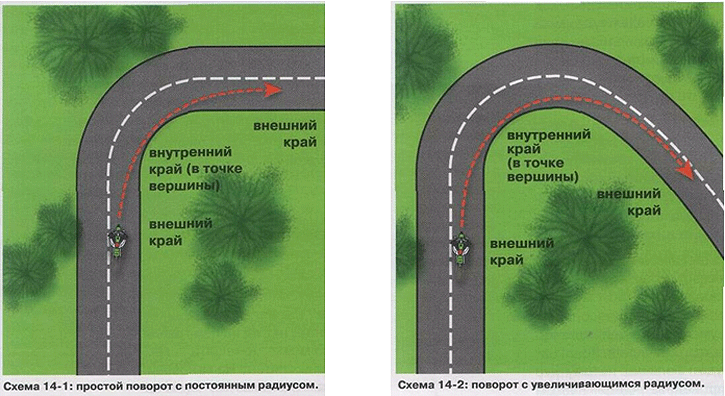 Для поворота на 90 градусов такому крупногабаритному транспортному средству требуется в 2 раза больше радиуса, чем европейским аналогам. Поэтому иногда приходится видеть такие ситуации, как на фото.

Неправильный разворот фуры

В городской черте такие автомобили не могут осуществлять безаварийное движение, чтобы постоянно не нарушать ПДД, затрудняют перемещение другого автотранспорта, т. к. их длина не соответствует европейским стандартам. Владельцы легковых автомобилей вынуждены держаться на расстоянии от «американцев», чтобы не попасть под удар разворачивающегося «монстра».

Как измеряем

Измерить радиус можно просто: отмечаем стартовое положение одного колеса (наружного), выворачиваем до конца рулевое колесо, разворачиваемся на полные 180 градусов, отмечаем конечное положение того же колеса. Между отметками замеряем расстояние, половина его и будет радиусом разворота. Этот размер является минимальной шириной дороги (именно гладкой части), которая позволит развернуться в один заход.

Это в теории, на практике же придётся учитывать и размер переднего свеса автомобиля, это расстояние от передней оси до кончика бампера. Дело в том, что ширина дороги не всегда ограничена низким бордюром, частенько бывают отбойники, а также сами бордюры могут быть до метра высотой. И если радиус разворота хорошо вписывается в идеальную дорогу, то с высокими ограничителями можно не вписаться. Так вот реальный радиус измеряется чуть сложнее – необходимо на наружной стороне бампера установить свес с мелом (можно на стержне), после разворота мел оставит отметки о реальном радиусе.

Радиус разворота на парковке

Рекомендуемые параметры расчетных автомобилей для Российской Федерации

Библиографическое описание:

Абдуназаров Ж. Н., Мамарасулова М. Н. Рекомендуемые параметры расчетных автомобилей для Российской Федерации // Молодой ученый. 2016. №7.2. С. 26-29. URL https://moluch.ru/archive/111/27588/ (дата обращения: 23.07.2019).

В связи с повышением динамических характеристик автомобилей совершенствуются требования к строительству и проектированию автомобильных дорог. При проектировании дорог возникает необходимость введения понятия «расчетный автомобиль». Этот термин определяется по-разному .

«Расчетный автомобиль – это транспортное средство, используемое для определения геометрических параметров автомобильных дорог (минимальные радиусы поворота пересечения в одном уровне, кольцевые пересечения), влияющих на безопасность, пропускную способность и стоимость пересечения. Это – условная транспортная единица, параметры которой используют в расчетах дорожной одежды и ее элементов».«Расчетный автомобиль – это такой автомобиль, массу, размеры и динамические качества которого используют при проектировании автомобильной дороги. Такие параметры расчетного автомобиля, как размеры и минимальный радиус поворота, должны быть такими же, как и у большинства других автомобилей этого же класса, которые предположительно будут использовать для движения проектируемую дорогу».

При проектировании автомобильных дорог и парковочных мест возникает необходимость определять ширину проездов, величину маневровых площадок, геометрические параметры. Это требует в каждом конкретном случае построения динамического габарита расчетных автомобилей, которое является процессом трудоемким (особенно для автопоездов) и не в достаточной мере освоенным проектировщиками.

Отсутствие систематизированного справочного материала по этим вопросам зачастую является причиной необоснованных проектных решений, которые либо ведут к завышению сметной стоимости объектов, либо не обеспечивают нормальных эксплуатационных условий работы автотранспорта.

Нами было исследован и изучен состав транспортных средств, передвигающихся по российским автомобильным дорогам, и разделен на следующие группы:

1. Легковой автомобиль;

2. Грузовой автомобиль;

Автобусы разделены на три типа: городской автобус, пригородный автобус, сочлененный автобус; автопоезда – два типа по длине.

Исходя из проведенных исследований нами были предложены параметры рекомендуемых расчетных автомобилей для проектирования автомобильных дорог. Были учтены не только длина и ширина расчетного автомобиля, но и база, передний свес, задний свес, который играет немаловажную роль при определении минимального радиуса автомобильной дороги (табл.1).

Размеры рекомендуемых расчетных автомобилей

Тип расчетного автомобилей

Прохождение поворотов

Умудренные опытом дальнобойщики чувствуют габариты автотранспортного средства, состоящего из тягача и полуприцепа с неуправляемой тележкой, а также возникающие сложности, связанные со смещением последней при вхождении в поворот.

Изящное прохождение перекрестка

Гораздо больше внимания водителю фуры требуется при выполнении маневрирования в черте города, где интенсивное движение пешеходов, а также легкового и общественного транспорта. Особо надо отметить сложности при проезде развязок и перекрестков – все необходимые маневры по изменению направления и смены полосы движения нужно выполнить заранее, но не ближе, чем за 20 метров от начала развязки или пересечения дорог.

Выполняя поворот направо, следует обратить внимание на встречную полосу дороги, т. к

автопоезд часто выезжает на нее, чтобы избежать заезда колесами тележки полуприцепа на бордюр, создавая угрозу травматизма пешеходов. При левом повороте не нужно стремиться проезжать центр перекрестка, потому что увеличивается площадь разворота, что затрудняет другому транспорту движение в нужную сторону.

Погрешности в повороте

Лонжерон автомобиля – конструкция, функционал, ремонт

Какой должен быть уровень антифриза: норма и тонкости проверки

Как поменять сальник распредвала: подробное пошаговое руководство

Какую жидкость лить в ГУР: разбираем все мифы

Шумоизоляция автомобиля: пошаговая инструкция + обзор материалов

Разбили стекло в автомобиле: кто виноват и что делать

Как снять датчик охлаждающей жидкости самостоятельно и заменить на новый

Заклинило колесо: что делать, если рядом нет СТО

Порядок ремонта насос-форсунок «Скания»

Ремонт рулевой рейки «Шевроле»: все не так страшно

Ремонт рулевой рейки «Опеля»: диагностика, профилактика, сервисное обслуживание

Ремонт рулевой рейки «Ауди»: диагностика и способы

Объем охлаждающей жидкости – важная характеристика технического состояния авто

Бескаркасные дворники: правила выбора и эксплуатации

Штраф за летнюю резину – есть ли он и какой?

Изменяем ли параметр

Отчего зависит радиус разворота? Во-первых, от габаритов авто, их поменять, разумеется, не получится. Во-вторых, от того, какой угол поворота у передних колёс. В общем, поменять радиус без серьёзного вмешательства в основную конструкцию не получится. А это потеря гарантии, а также возможные проблемы со стабильной работой. Обычно такие переделки можно встретить на машинах для дрифта, где выворот делают максимальным. Правда, это делается не для уменьшения радиуса разворота, а для увеличения угла заноса, который может держать машина. Обычные гражданские машины лучше не переделывать.

Статья написана по материалам сайтов: moluch.ru, www.drive2.ru, autowestnik.ru.

Что такое радиус поворота

Многие автолюбители «не в теме», и редко кто из них знает, что такое радиус поворота фуры. Согласно специальной технической литературе – это воображаемая дуга, по линии которой перемещается центр тяжести тягача с полуприцепом при выполнении сложного маневрирования. Максимальное значение этой величины (радиуса) во многом зависит от специфической конструкции транспортного средства.

Вот как фура во время поворота может зацепить своим полуприцепом легковой автомобиль:

Есть специальный термин – расчетный автомобиль, его тактико-технические показатели используются при разработке проектов трасс регионального значения. Такие параметры, например: размер и R min поворота должны быть идентичными у каждого класса автотранспорта.

Нормы европейского стандарта регламентируют следующие габариты для автотранспорта большегрузной категории во время движения на поворотах:

  • при R наружном в 12,5 м – R внутренний будет равен или меньше 5,3 м;
  • коридор для вписывания в поворот – 7,2 м;
  • R min наружный не должен превышать 12,5 м.

Например: для автопоезда типа А16, имеющего линейный размер до 16 метров, и аналогичного вида А20 с длиной до 20 м прописаны строгие ограничения, указанные в приведенной ниже таблице:

Тип автомобиляR min поворота, мR min внешний, мR min внутренний, м
А169,710,26,2
А2012,112,68,5

Типичными прототипами для расчетных автомобилей могут служить:

  • автопоезд до 16 м – MAN F-200019. 403 FLT или европейская фура с габаритами 16,5 × 2,5 м, где первый параметр – линейный, а второй – ширина;
  • 20-метровый вариант – «Мерседес-Бенц Актрос» или СЗАП-8357А, с габаритами 19,8 на 2,5 м.

Автопоезда с двумя или тремя прицепами, имеющие длину больше 20 метров, используются всеми перевозчиками мира, поэтому при разработке макетов автотрасс нужно проводить дополнительное компьютерное моделирование такого специфического движения во время поворотов на пересечениях дорог или городских перекрестках.

Автопоезд на дороге

Список источников

  • yvezi.ru
  • rad-star.ru
  • the-avto.ru

ДБН В.2.3-4-2000. . Автомобильные дороги. (На русском языке) /Отменен-приказ Минрегионбуду Украины N 292 от 31.10.2007р./ (43044)

2.19 Если по условиям рельефа и другим местным условиям невозможно выполнить требования 2.18 или выполнение их связано со значительными объемами работ и стоимостью строительства, при проектировании дорог допускается снижать нормативные параметры к предельно допустимым, определенным соответственно расчетным скоростям по таблице 2. 2 и таблице 1.3.

При проектировании участков дорог в горной местности Карпат и Крыма на подходах к туннелям максимальный продольный уклон проезжей части не должен превышать 45 ‰ на участке 250 м от портала туннеля.

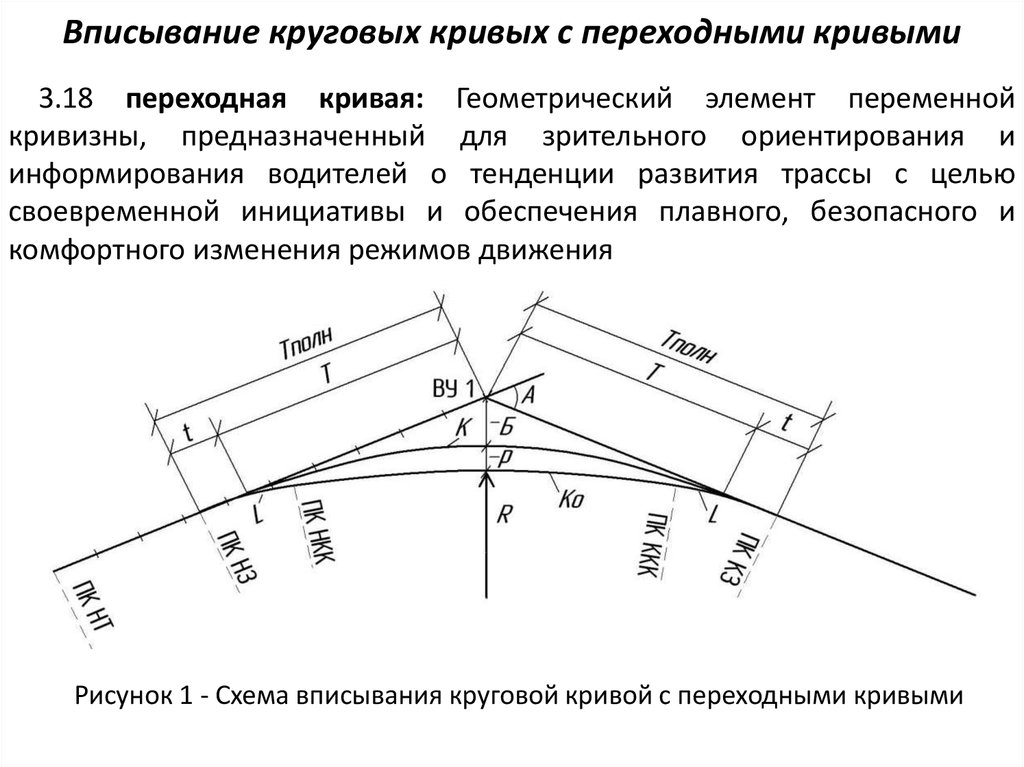
2.20 Переходные кривые следует предусматривать при радиусе кривой в плане 2000 м и менее. Минимальную длин]/ переходной кривой следует принимать по таблице 2.8.

Таблица 2.8 — Минимальные длины переходных кривых

В метрах

Радиус круговой кривой

30

50

60

80

100

150

200

250

300

400

500

600-1000

1000-2000

Длина переходной кривой

30

35

40

45

50

60

70

80

90

100

110

120

100

2. 21 Максимальный продольный уклон на кривой в плане с радиусом <—50 м следует уменьшать к значениям, приведенным в таблице 2.9.

Таблица 2.9 — Уменьшение продольных уклонов автомобильных дорог на горизонтальных кривых

Радиус кривой в плане, м

50

45

40

35

30

Уменьшение максимального продольного уклона по сравнению с приведенными в таблице 2.2, не менее, %

10

15

20

25

30

2.22 Ширину полос расчистки леса и кустов, величину срезки откосов выемок и расстояние переноса строений на участках кривых в плане с внутренней стороны для обеспечения расчетной видимости следует определять расчетом. Срезку откосов выемок следует выполнять на уровне бровки земляного полотна согласно ДСТУ 3587.

2.23 На сложных участках дорог в горной местности допускаются затяжные уклоны (свыше 60 ‰) с обязательным устройством участков с уменьшенным продольным уклоном (до 30 ‰) или устройством площадок для остановки автомобилей или дополнительных полос для остановки автомобилей на расстоянии не более длины участков, приведенных в таблице 2.10.

Таблица 2.10 — Длина участков с затяжным уклоном в горных условиях

Продольный уклон,‰

Длина участка, при высоте над уровнем моря (не более), м

до 1000

до 2000

60

2500

2200

70

2200

1900

80

2000

1600

90

1500

1200

Размеры площадок для остановки автомобилей определяются расчетом, но они должны вмещать не менее трех автопоездов длиной 22 м каждый. Выбор места их расположения определяется исходя из условий безопасности остановки, желательно в 15 местах за пределами появления осыпей, камнепадов и т.п.

Независимо от наличия площадок для остановки автомобилей на затяжных спусках с уклонами свыше 50 ‰ следует проектировать противоаварийные съезды в зоне кривых с радиусами <100 м (кроме серпантин), в конце спуска, а также на прямых участках спуска через каждые 0,8-1,0 км. Элементы противоаварийных съездов определяют расчетом для безопасной остановки автопоезда.

2.24 На крутых горных склонах целесообразно прокладывать дорогу серпантинами. Нормы проектирования серпантин следует принимать по таблице 2.11.

Таблица 2.11- Нормы проектирования серпантин

Параметр элемента серпантины

Норма проектирования серпантины при расчетной скорости движения, км/час

30

20

15

Минимальный радиус кривой в плане, м

30

20

15

Поперечный уклон проезжей части на вираже, %0

60

40

30

Длина переходной кривой, м

30

25

20

Уширение проезжей части, м

2,2

3,0

3,5

Максимальный продольный уклон на участках серпантин, ‰

30

35

40

Серпантина радиусом менее 30 м разрешается только на дорогах IV и V категорий при запрете движения транспортных средств с габаритами по длине более 11 м.

2.25 Расстояние между концами кривых двух соседних серпантин следует назначать не менее 400 м для дорог II и III категории, 300 м — для дорог IV категории и 200 м — для дорог V категории.

2.26 Проезжую часть на серпантинах допускается уширять на 0,5 м за счет внешней обочины, а остаток уширения — за счет внутренней обочины и дополнительного расширения земляного полотна.

2.27 Кривые в плане и продольном профиле целесообразно совмещать. При этом кривые в плане должны быть на 100-150 м длиннее кривых в продольном профиле.

Следует избегать соединения концов кривых в плане с началом кривых в продольном профиле. Расстояние между ними рекомендуется назначать не менее 150 м.

2.28 При малых углах поворота дороги в плане радиусы круговых кривых рекомендуется принимать по таблице 2.12.

Таблица 2.12 — Радиусы горизонтальных кривых при малых углах поворота

Угол поворота, град

1

2

3

4

5

6

7-8

Минимальный радиус круговой кривой, м

30000

20000

10000

6000

5000

3000

2500

2. 29 Если кривая в плане расположена в конце спуска длиной свыше 500 м и с уклоном свыше 30‰, радиус ее должен быть увеличен не менее чем в 1,5 раза по сравнению с величинами, приведенными в таблице 2.12, с совмещением кривой в плане и вогнутой кривой в продольном профиле в конце спуска.

2.30 Не рекомендуется короткая прямая вставка между двумя кривыми в плане, которые направлены в одну сторону. При ее длине менее 100 м рекомендуется заменить обе кривые одной кривой большего радиуса. При длине 100-300 м прямую вставку целесообразно заменять переходной кривой большего радиуса. Прямая вставка как самостоятельный элемент трассы допускается для дорог I и II категорий при ее длине свыше 700 м, для дорог III и IV категорий — свыше 300 м.

2.31 Не желательно допускать длинных прямых вставок в продольном профиле, максимальные предельные их длины приведены в таблице 2.13.

Таблица 2.13 — Предельные длины прямых вставок в продольном профиле

Радиус вогнутой кривой в продольном профиле, м

Максимальная длина прямой вставки в продольном профиле при алгебраической разности продольных уклонов, ‰

20

30

40

50

60

80

100

Для дорог I и II категорий

4000

150

100

50

—

—

—

—

8000

360

250

200

170

140

110

—

12000

680

500

400

350

250

200

—

20000

—

—

850

700

600

550

—

25000

—

—

—

—

900

800

—

Для дорог III и IV категорий

2000

120

100

50

—

—

—

—

6000

550

440

320

220

140

60

—

10000

—

—

680

600

420

300

200

15000

—

—

—

—

—

800

600

Велосипедные дорожки и тротуары

2. 32 Велосипедные дорожки следует проектировать вдоль автомобильных дорог на участках, где интенсивность движения велосипедов за первые пять лет эксплуатации дороги достигнет в одном направлении 60 и более велосипедов за час при максимальной интенсивности движения или 400 единиц в сутки. Велосипедные дорожки, как правило, проектируют для одностороннего движения шириной не менее 1,5 м, а для двухстороннего — не менее 2,2 м на обособленном земляном полотне, возле подошвы насыпи или за пределами откосов выемок, а также на специально построенных бермах или полках.

Велосипедные дорожки с одной полосой для движения в обоих направлениях, следует размещать с подветренной стороны дороги (в расчете на преобладающие летом ветры), а велосипедные дорожки, состоящие из двух полос для движения в противоположных направлениях, следует размещать в отдельности с обеих сторон дороги. В стесненных условиях и на подходах к искусственным сооружениям разрешается строительство велосипедных дорожек на обочине.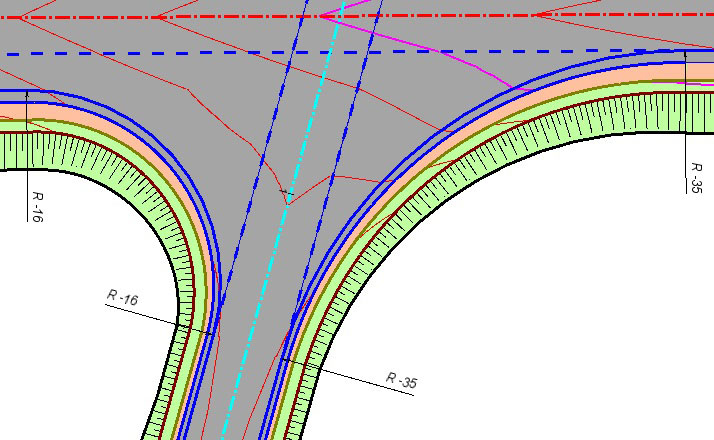 В таких случаях обочину следует отделять от проезжей части бордюром высотой 0,20 м, а расстояние между ближними кромками велосипедной дорожки и проезжей части дороги (вертикальной гранью бордюра) должна быть не менее 1,5 м.

2.33 Велосипедная дорожка, если она является самостоятельным объектом, проектируется в индивидуальном порядке.

2.34 Велосипедные дорожки в зоне развязок следует прокладывать за пределами земляного полотна дорог. Проезжую часть автомобильных дорог велосипедные дорожки должны пересекать под углом (90±10°).

При пересечении автомобильной дороги велосипедная дорожка на расстоянии по 3 м с каждой стороны от кромки проезжей части должна быть прямой в плане.

2.35 Пешеходные переходы в различных уровнях следует проектировать через дороги Iа категории, а — Iб-II категорий при интенсивности пешеходного движения свыше 200 чел./час.

2.36 При проектировании пешеходных дорожек в зоне развязок руководствуются теми ж правилами, что и при проектировании велосипедных дорожек.

2.37 На подходах к путепроводу через железнодорожные пути с обеих сторон проезжей части проектируют пешеходные дорожки с учетом, при обосновании, возможности движения по ним велосипедов и инвалидных колясок. Длину дорожки назначают равной расстоянию от начала подъема на путепровод до начала путепровода.

3 ДОРОЖНЫЕ РАЗВЯЗКИ, ПЕРЕСЕЧЕНИЕ АВТОМОБИЛЬНЫХ ДОРОГ С ИНЖЕНЕРНЫМИ КОММУНИКАЦИЯМИ

3.1 Развязки на пересечениях и примыканиях автомобильных дорог (далее — дорожные развязки) должны обеспечивать максимальную безопасность и удобство движения транспортных средств с минимальными затратами времени при их проезде.

3.2 Дорожные развязки следует проектировать на основании перспективной интенсивности движения и состава транспортных потоков во всех направлениях.

3.3 Выбор типа и схемы дорожных развязок и обоснование технических решений выполняют на основании технико-экономического сравнения вариантов с учетом их пропускной способности, безопасности и удобства движения, дорожно-транспортных затрат на их строительство и эксплуатацию, архитектурно-эстетических требований и требований охраны окружающей среды, рационального использования близлежащих земельных участков.

3.4 Дорожные развязки в зависимости от суммарной интенсивности движения на них делятся на классы согласно таблице 3.1.

Скачать бесплатно

Цельные твердосплавные концевые фрезы — HARVI™ I TE • РАДИУС СКРУГЛЕНИЯ • 4 зуба • С шейкой • Хвостовик Weldon®

Предложения по продукции

Product Family suggestions

ВЫЙТИ ИЗ ПОИСКА

Вернуться к решению

  • продукты
  • /
  • HARVI™ I TE • РАДИУС СКРУГЛЕНИЯ • 4 зуба • С шейкой • Хвостовик Weldon®
  • /
  • HARVI™ I TE • РАДИУС СКРУГЛЕНИЯ • 4 зуба •
    С шейкой • Хвостовик Weldon®

Загрузка чертежей САПР

SDS

HARVI™ I TE • РАДИУС СКРУГЛЕНИЯ • 4 зуба • С шейкой • Хвостовик Weldon®

Метрическая система

Дюймовая система

SAP Material Number6676284
ISO Catalog Numberh2TE4RA1600N024HBR100M
ANSI Catalog Numberh2TE4RA1600N024HBR100M
GradeKCSM15
Adapter Style Machine SideWeldon
[D1] Effective Cutting Diameter16. 0000 mm
[D1] Effective Cutting Diameter.6299 in
[D] Adapter / Shank / Bore Diameter16.0 mm
[D] Adapter / Shank / Bore Diameter.6299 in
[D3] Neck Diameter15.0400 mm
[D3] Neck Diameter.5921 in
[AP1MAX] 1st Maximum Cutting Depth24.0000 mm
[AP1MAX] 1st Maximum Cutting Depth.9449 in
[L3] Usable Length48.0000 mm
[L3] Usable Length1. 889 in
[L] Overall Length100.0000 mm
[L] Overall Length3.937 in
[Re] Corner Radius1.0000 mm
[Re] Corner Radius.0394 in
[Z] Number of Flutes4
Посмотреть все варианты продукции

Использование и область применения

  • Slotting: Square End
  • Trochoidal Milling
  • Tool Dimensions: Flute Configuration: 4
  • Helical Milling
  • Pocketing
  • Ramping: Blank
  • Side Milling/Shoulder Milling: Eased Chamfer
  • Plunge Milling
  • Side Milling/Shoulder Milling: Roughing
  • Shank — Cylindrical Weldon
  • Corner Style: Corner Radius
  • 100147465

Обрабатываемый материал

P Steel

M Stainless Steel

K Cast Iron

S High-Temp Alloys

H Hardened Materials

Характеристики и преимущества

  • Versatile solid carbide end mill for steels, stainless steel, cast iron, and high temperature alloys.

  • HARVI™ I TE solid carbide end mills cover a variety of operations, including dynamic milling, and extreme ramping operations.

  • HARVI™ I TE solid carbide end mills stand for maximum metal removal, maximum productivity, maximum benefit.

  • HARVI™ I TE solid carbide end mills feature asymmetrical divided flutes, variable helix, twisted end face, facteted eccentric relief, and chip gashes within the flutes.

  • Centre cutting for plunging and ramping operations.

{{name}}

{{#if ../commerceEnabled}} {{#if purchasable}}

Цена по прейскуранту:

Скидка: %

Ваша цена::

/упаковка. (упаковка из )/каждый.

Войдите в систему, чтобы увидеть цену

{{#if replacementProductUrl}}

Замена Данный товар недоступен
Продукция для замены {{replacementProductCode}} Данный товар можно приобрести у дистрибьютора

{{/if}}

Кол-во

Продается в упаковке из

Извините! У нас нет такого количества в наличии. Сегодня у нас есть только:

Корректируется в соответствии с минимальным размером упаковки.

{{/if}} {{/if}}

{{/each}}

Со стороны станка

загрузка…

Со стороны заготовки

загрузка…

  • Совместимые детали
  • Сплавы
  • TechnicalInfo
  • Режимы резания

Сплавы

  • Coated carbide grade with thick PVD coating and optimized chemistry
    and process for increased wear resistance. Outstanding protection in milling stainless steel to mitigate crater, DOCN (depth-of-cut notching), and flank wear. Excellent performance up to 52 HRC.

    P Steel

    S High-Temp Alloys

    H Hardened Materials

    K Cast Iron

    M Stainless Steel

Поддержка

Купить

Купить товары с фирменной символикой Kennametal

Найти нас на Ariba

Вакансии

✉ Оставайтесь на связи

⤓ приложение NOVO

Найдите замену устаревшим инструментам

© 2022 Terms & Conditions of Use | Conditions of Sale | Data Privacy Policy

Kennametal Inc. 525 William Penn Place Suite 3300, Pittsburgh, PA 15219

  • Найти решение
  • Избранное
  • Найти ближайшего дистрибьютора
  • Чат
  • Поддержка
  • Каталоги

Please adjust the following properties from

Номер по каталогу ISO

Номер по каталогу ANSI

to find similar products.

Совместимость решений

Вы собираетесь создать дубликат . Хотите продолжить?

Вы собираетесь удалить Хотите продолжить?

Как вы хотите переименовать ?

Фамилия

Введите действительное имя

Введите имя дубликата

Введите имя дубликата

Введите действительное имя

Вы собираетесь добавить на страницу «Мои решения». Хотите продолжить?

Create Name

Введите действительное имя

Отправить копию

Кому:

Введите действительный адрес электронной почты

Решение Фамилия:

Введите действительное имя

{{/each}}

Найдены следующие чертежи САПР

Выберите файлы, которые вы ищете, и загрузите их одновременно

Вы должны войти в систему, чтобы увидеть информацию на панели мониторинга

Session expired due to inactivity, please login again

Товары (), которые вы пытались добавить в корзину, недоступны, обратитесь в центр обслуживания клиентов.

товар(-ы) успешно добавлен(-ы) в корзину

Показать корзину

Корзина

Всего: {{subTotal.formattedValue}}

Позиция

Количество

Стоимость

Итого

{{#each entries}}

{{product.name}}

Номер изделия{{product.code}}

{{basePrice.formattedValue}} /{{#ifpkg packageQty}}упаковка {{else}}каждый {{/ifpkg}}

Номер по каталогу{{product.catalogISO}}

Количество: {{quantity}}

{{quantity}}

{{basePrice.formattedValue}} /{{#ifpkg packageQty}}упаковка {{else}}каждый {{/ifpkg}}

{{totalPrice.formattedValue}}

{{else}}

Ваша корзина пуста, Продолжить покупки

{{/each}}

Проектирование примыканий к автомобильным дорогам: обзор правил и норм

В этой статье:

  • Проектирование примыканий к автомобильным дорогам
  • Требования к примыканиям и пересечениям автомобильных дорог
  • Виды примыканий и разветвлений автомобильных дорог
  • Необходимость экспертизы при создании примыкания автомобильной дороги

Проектирование примыканий к автомобильным дорогам – это необходимый комплекс мероприятий, который проводится перед началом строительства объекта. Без проведения проектных работ законодательно запрещено эксплуатировать дорогу (примыкание, съезд, пересечение и т. д.).

Для создания качественного проекта необходимо обратиться к специалистам, имеющим соответственный опыт. В нашей статье мы расскажем, какие бывают примыкания дорог, поговорим о требованиях, которые предъявляются к ним, и затронем вопрос о необходимости экспертизы.

Проектирование примыканий к автомобильным дорогам

Действующие требования российского законодательства в отношении строительства или реконструкции автотранспортных магистралей и примыкающих к ним объектов предусматривают составление определенной проектной документации.

Проектирование объектов примыканий к автомобильным дорогам предполагает создание расчетных документов для сооружения:

  • Автозаправочных комплексов.
  • ТРЦ.
  • Новых съездов/въездов.
  • Транспортные развязки.
  • Площадки под строительство.
  • Объекты малого бизнеса и т.д.

Перед тем, как приступить к разработке проекта необходимо изучить технические условия и создать первоначальный план документации в соответствии с нормами законодательства.


Стандартные рабочие процедуры, в перечень которых входит составление необходимой документации для проектов строительства или реконструкции пересечений и примыканий автомобильных дорог:

  • Создание полного генерального плана будущего объекта строительства или реконструкции, соединенного с автомобильной дорогой.
  • Составление сводного сборочного плана всех основных инженерных коммуникаций, необходимых для полноценного функционирования обслуживаемого объекта.
  • Полоса для отведения линейных объектов (электропередач, связи).
  • Создание и подтверждение условия технического состояния.
  • В зависимости от объекта строительства или реконструкции собирается дополнительная документация и разрешения в соответствующих структурах власти (определяется в индивидуальном порядке).

В процессе сбора документации и накопления информации для полного согласования и утверждения всех работ по строительству или реконструкции необходимо посетить определенные государственные учреждения.

Основной список государственных организаций и структур для получения официального документационного утверждения:

  • Районная администрация;
  • Районная префектура;
  • отдел ГИБДД;
  • ЦОДД;
  • Сетевые учреждения.

На утверждение технических нормативов проектной и прочей документации влияют вид предстоящих работ (строительство/реконструкция), тип обслуживаемого объекта и остальные особенности.


Требования к примыканиям и пересечениям автомобильных дорог

В Своде Правил (СП 34.13330.2012) об автомобильных дорогах можно найти основные требования, предъявляемые к примыканиям и пересечениям автодорог. Обновленная информация содержится в СНиП 2. 05.02-85.

Это интересно!

“Виды малоэтажного строительства: разбираемся в классификации”

Подробнее

В 6 пункте Свода Правил установлено, что проектирование пересечений и примыканий автомобильных дорог зависит от их типа, а также разновидностей транспортных средств. В процессе создания проекта прогнозируют повышение интенсивности движения потока ТС, поэтому оставляют возможность стадийного развития.

Также в Своде Правил утверждено, для каких категорий дорог разрешено проектирование пересечений и примыканий: оно возможно на прямых и кривых дорогах.

  • для не скоростных дорог с двумя полосами (тип III и IV) радиус поворота начинается от 0,8 км;
  • для автомагистралей, скоростных участков и не скоростных дорог с четырьмя полосами (тип IA, IБ, IB и II) радиус поворота должен составлять не менее 2 км.

В таблице из Свода Правил автомобильных дорог (п.5.9) установлено, что уклоны в продольной плоскости при подъезде к примыканиям и пересечениям автомобильных дорог должны быть не выше 40 ‰. В таком случае будет сохранено безопасное движение автомобилей при поворотах, разгонах, снижении скорости или смене полос.

В представленной ниже таблице указаны минимальные расстояния видимости при различных скоростях движения. Они указаны в соответствии со Сводом Правил, в котором определено, что расстояние видимости равно расстоянию остановочного пути.

Скорость движения (км/ч)

Минимальное расстояние видимости в м

для остановки

встречного автотранспорта

при обгоне

150

300

—

—

120

250

450

800

100

200

350

700

80

150

250

600

60

85

170

500

50

75

130

400

40

55

110

—

30

45

90

—

20

25

50

—

Водитель должен иметь возможность определить очертания любых объектов посередине полосы движения с высоты одного метра от дорожного покрытия. Размер предметов начинается от 0,2 метра, тогда безопасный тормозной путь будет обеспечен. Два параметра (расчетная скорость и расстояние видимости) главным образом влияют на расположение элементов при планировании как в вертикальном разрезе дороги, так и в горизонтальном.

Если строительство пересечений и примыканий автомобильных дорог к тоннелям проводится в местностях с горным рельефом, необходимо обеспечить условия видимости объектов исходя из установленной скорости движения.

Пункт 6 Свода Правил автомобильных дорог определяет разновидности пересечений и примыканий при создании проекта. В итоге дороги делятся на главные и второстепенные в категориях автомагистралей, скоростных и не скоростных дорог (включительно до III категории). Здесь число разветвлений и пересечений не может быть велико. На автомагистралях (не на территории населенных пунктов) пересечения и примыкания автомобильных дорог могут появляться только каждые 10 км. На скоростных трассах и дорогах категории II расстояние уменьшается в два раза, что позволяет строить разъезды каждые 5 км. На не скоростных дорогах III типа присутствуют условия, которые необходимо учитывать (строительство объектов, особенности дорог). Тогда пересечения и примыкания могут появляться каждые 2 км.

Это интересно!

“Последовательность этапов проектирования: от сбора разрешительной документации до проведения экспертизы”

Подробнее

Как утверждено в пункте 6 Свода Правил постоянные примыкания к скоростным и не скоростным (до категории III включительно) дорогам могут иметь:

  • грунтовое покрытие из тяжелых суглинистых пород, чернозема и глины на 200 метров;
  • грунтовое покрытие из легких суглинистых пород и песка на 100 метров.

Обочины в описанных выше категориях дорог должны быть укреплены на указанную длину. Ширины составляет до 0,75 м.

Расстояние покрытия съездов и въездов на скоростных и не скоростных (до категории III включительно) дорогах в два раза больше, чем на не скоростных дорогах с двумя полосами.

Виды примыканий и разветвлений автомобильных дорог

Примыкания на транспортных развязках могут быть разного вида, поэтому часто они встречаются в виде разветвлений. Что касается характеристик безопасности или комфорта передвижения, разветвления показали себя с наилучшей стороны.

В некоторых случаях предусмотрено использование исключительно разветвления на дорогах определенного уровня.

Для проектирования разветвлений или примыканий прямого типа, как «трубы», используют схему строения «клеверного листа». Каждый транспортный поток имеет отдельный съезд, чтобы при поворотах они не смешивались. Что касается съездов левоповоротного типа, там предусмотрен достаточно длинный путь, выполненный в виде двухполюсной дороги. Автомобили движутся в обоих направлениях, пока окончательно не разъедутся.


У путепровода левоповоротный съезд не должен располагаться только слева. Он может быть выполнен с правой стороны в зависимости от особенностей территории. Определяющим фактором является интенсивность движения транспорта.

Если говорить о безопасности движения на автомагистралях, левоповоротный съезд листовидного типа является относительно спокойным. На одном уровне не пересекаются транспортные средства разных потоков. Однако на отрезке общего земляного полотна появляется движение в обе стороны, что вызывает некоторую опасность на дороге. При выезде на автомагистраль транспортный поток присоединяется к основному исключительно справа. Потоки противоположного направления в данном случае никак не смешиваются.

Потоки правого и левого поворота не пересекаются друг с другом. Левоповоротный поток входит в главный транспортный поток. Водители не испытывают затруднений при выполнении разъездов или съездов, поскольку схема развязок логична. В отличие от примыкания «трубы» здесь потребуется больше квадратных метров для обустройства дороги.

Транспортная развязка типа клеверного листа имеет минус, поскольку на одном уровне дорог находится точка, в которой два потока смешиваются.


Достоинства:

  • водители транспортных средств интуитивно понимают схему строения развязки, поскольку ее схема проста;
  • в процессе развязки поворот транспорта может быть, как вправо, так и влево при левоповоротном движении.

Широкое распространение нашли и кольцеобразные развязки. К ним относятся два вида разветвлений: грушевидный и кольцевой. За основу берется распределительное кольцо, по которому и строится разветвление или примыкание автомобильных дорог. Также предусмотрено два путепровода. Транспортный поток въезжает на кольцо справа, затем вливается обратно в главный поток магистрали также с правой стороны. При правоповоротном съезде кольцо присоединяется слева. При кольцевом движении левоповоротные потоки начинают смешение. Здесь водители также не испытывают затруднений в процессе движения.

В отличие от вышеописанного вида разветвлений в грушевидном типе за основу берется турбинное пересечение. Важное отличие, что потоки левого поворота не пересекаются между собой, поскольку каждый из них имеет отдельный съезд. Движение более безопасное и спокойное. Автомобили, начинающие вливание на основную часть магистрали, делают это справа. Примыкание левоповоротного съезда к правоповоротному происходит слева. В данном случае грушевидный тип примыканий и разветвлений также имеет простую конфигурацию, которая понятна водителю.

Существуют другие разновидности разветвлений и примыканий:

  • грибообразный — также имеет в основе элемент кольца;
  • линейный;
  • крючкообразный;
  • лирообразный;
  • тип криволинейного треугольника с одним путепроводом;
  • V-образный.

Необходимость экспертизы при создании примыкания автомобильной дороги

Заказчик, которому требуется проектирование пересечений и примыканий автомобильных дорог к придорожному объекту (чаще всего это автозаправки, кафе или хостелы, станции техобслуживания, магазины, в редких случаях могут быть аэродромы или площадки для воздушного транспорта), имеет цель не просто построить сервисное здание, но и обеспечить ему условия для функционирования и удобный проезд.

Подключить дорожный съезд к официальному использованию можно только при условии, что имеется разрешение на его возведение. Процедура оформления занимает некоторое время, поскольку требуется создание проекта, проведение экспертизы пакета документов. В зависимости от источника финансирования тип проверки будет отличаться. При использовании средств бюджета понадобится государственная экспертиза проектной документации и процесса возведения объекта. Если средства из частного источника — достаточно негосударственной проверки. В итоге будет принято заключение:

  1. Вынесение положительного решения экспертизой в отношении проектной документации.
  2. Согласование проекта межевания и планировки земельного участка, взятого под строительство объекта.
  3. Установление отношений по территории (временная аренда или полное владение).

Перечисленные результаты относятся только к объектам линейных коммуникаций (линии железной дороги, мосты, электропровод и т. п.).

В некоторых случаях экспертиза не является обязательной, если будущее примыкание планируется строить в границах установленной полосы отвода. Тогда подается обращение к владельцу главной дороги, чтобы утвердить проект съезда. В основном заявка идет в РосАвтоДор. Далее запрашиваемое разрешение получит необходимые технические условия, после которых можно начинать строительство. Не забываем про переходно-скоростные полосы.

Прохождение экспертизы и утверждение проектной документации являются обязательным условием, если строительство съезда будет выходить за отведенные границы отвода. Процедура должна быть выполнена, поскольку владелец главной дороги в таком случае не является ответственным за проведение работ лицом. Его внимание распространяется только до конца территории полосы отвода. Не забываем о постановке участка на кадастровый учет. Застройщик создает проект планировки территории, проект межевания и затем разрабатывает градостроительный план. Необходимо изучить весь периметр участка, чтобы со всей документацией обращаться на экспертизу.

Как это работает – Кривизна

Хотя я добился определенных успехов в поиске интересных дорог на карте, одним из недостатков бумажной карты является то, что крутые изгибы, на которые можно опереться, имеют тенденцию быть ниже разрешения, отображаемого на карте. страница. Бумажные атласы и электронные карты позволяют вам увеличивать масштаб, чтобы увидеть больше деталей, но тогда возникает проблема поиска жемчужин в море данных. Я понял, что мне нужен способ выделить только самые извилистые дороги, чтобы я знал, куда идти дальше.

Для тех, кто менее знаком с пересечением картографии и программного обеспечения, электронные картографические системы мира (ваш Garmin/TomTom GPS, OpenStreetMap, Google Earth, MapQuest, Bing Maps и т. д.) имеют базы данных, в которых хранятся последовательности тысяч координат, которые связаны между собой, определяют пути дорог по поверхности земли.

В то время как большинство этих систем основаны на проприетарных наборах данных, недоступных для всех без бюджета крупной корпорации, проект OpenStreetMap (OSM) представляет собой общедоступный набор данных, который отображает весь мир. OpenStreetMap — это проект сообщества, который может добавлять и редактировать каждый — Википедия для картографических данных. В некоторых частях мира Open Street Map имеет лучшее покрытие, чем любые коммерческие поставщики; в США исходные данные были импортированы из общедоступного набора данных USGS TIGER, а затем были расширены и улучшены сообществом.

Я могу получить необработанные данные из OpenStreetMap для каждой дороги, но как определить, какие из них самые извилистые? Вначале я пробовал такие стратегии, как вычисление отношения пройденного расстояния по дороге к расстоянию между начальной и конечной точками. К сожалению, во всех этих первоначальных методах были ситуации, которые путали алгоритмы (например, кольцевые дороги) или не различали забавные кривые и скучные широкие изменения направления, которые были бы захватывающими только при превышении ограничения скорости. В конце концов я придумал процесс вычисления радиуса кривизны на каждом сегменте каждой дороги, а затем суммирования длины самых извилистых сегментов, чтобы получить общее расстояние, затрачиваемое на повороты. Чем извилистее дорога, тем больше расстояние (и времени) тратится на повороты.

Curvature — это небольшая программа командной строки, которая считывает данные OpenStreetMap и анализирует форму каждой дороги. Он берет эти результаты и отфильтровывает все, кроме самых извилистых дорог, которые затем выводятся в базу данных карт и файлы KML (Google Earth). Исходный код Curvature доступен на Github здесь: https://github.com/adamfranco/curvature

Расчет кривизны дороги

Как упоминалось выше, каждый путь (дорога) состоит из последовательности точек. определяется как пара значений широты и долготы. Каждая последовательность из трех точек образует треугольник, две стороны которого являются сегментами дороги с гипотенузой между 1-й и 3-й точками. Поскольку у нас есть широта и долгота каждой точки, мы можем легко вычислить расстояния между ними, но выяснить, какова кривизна дороги в этом наборе точек, немного сложно. Поскольку точки расположены неравномерно, угол между тремя точками нам ничего не говорит. Вместо этого мы должны обратиться к геометрическому соотношению, согласно которому для каждого треугольника существует описанная окружность, пересекающая три его точки. Используя уравнения для описанной окружности, мы можем подставить расстояния между тремя точками и получить радиус этой окружности. Радиус этого круга соответствует радиусу кривой дороги в середине трех точек.

Вот видео, объясняющее процесс:

После того, как радиус кривой для каждого сегмента был рассчитан, мы можем пройтись по каждому сегменту и классифицировать его по нескольким группам:

  • Повороты с большим радиусом, которые мы рассмотрите «прямой» и дайте вес «0».
    (зеленые сегменты на изображении ниже)
  • Широкие, широкие повороты, которым мы присвоим вес «1».
    (желтые сегменты на изображении ниже)
  • Более крутые повороты, которым мы присвоим вес «2».
    (оранжевые сегменты на изображении ниже)
  • Сверхплотные углы, которым мы присвоим вес «4».
    (красные сегменты на изображении ниже)

Так как пронумерованные автомагистрали могут иметь протяженность в сотни и тысячи миль, из которых только часть извилистая, каждая дорога впоследствии разбивается на участки, если она проходит более двух миль без поворотов. которые выталкивают сегмент из прямого ведра. Этот процесс разделения позволяет выделять только извилистые участки без примыкания к ним длинных прямых участков.

Разделив каждый сегмент на взвешенное ведро, мы можем затем умножить длину каждого сегмента на его вес и суммировать взвешенные длины в одно число. Это число представляет собой значение кривизны участка дороги и примерно соответствует количеству километров, на которое мотоцикл наклоняется в поворот при движении по участку дороги.

После того, как для каждого участка дороги будет рассчитано значение кривизны , весь набор данных фильтруется для удаления любых участков дороги ниже заданного порога. В карте и загрузках KML я указываю два порога: кривизна ≥ 1000 и кривизна ≥ 300. Дороги в наборе данных имеют цветовую кодировку в диапазоне от желтого (наименее извилистая) до розового (наиболее извилистая).

Что такое значений кривизны ?
Кривизна Значения представляют собой взвешенную меру длины кривых проезжей части (выраженную в метрах). Основываясь на своем опыте просмотра данных и езды по дорогам, я обнаружил, что значения кривизны регулярно коррелируют с тем, насколько мне нравится ездить по дороге — при хорошем дорожном покрытии, малом трафике и не слишком большом количестве остановок. знаки.
  • кривизна : < 300
    На них может быть несколько забавных поворотов, но эти дороги преимущественно прямые или имеют большие расстояния между каждым значительным поворотом.
  • кривизна : 300-1,000
    Эти дороги имеют несколько важных поворотов, расположенных близко друг к другу. Скорее всего, они не являются туристическими направлениями, если только вы не застряли на прямых дорогах в регионе, но если вы хотите оживить свои поездки несколькими поворотами, это может быть интереснее, чем самый прямой маршрут.
  • кривизна : 1,000-3,000
    В этом диапазоне много интересных дорог. Обычно они имеют несколько десятков углов и обычно кажутся более извилистыми, чем прямыми.
  • кривизна : 3,000-10,000
    Для большей части мира этот диапазон включает дороги назначения, по которым люди могут ездить часами, чтобы посетить. Эти дороги обычно имеют длинные участки крутых поворотов, часто на несколько миль подряд. На северо-востоке США все лучшие дороги находятся в этом диапазоне.
  • кривизна : 10,000+
    Это поистине эпические дороги с милей за милей изгибов и поворотов.

Помимо фильтрации «прямых» дорог, Кривизна также будет отфильтровывать грунтовые дороги, которые идентифицируются по тегу поверхности в OpenStreetMap. К сожалению, на момент написания этой статьи большая часть мира не имеет универсального охвата поверхностных тегов, поэтому Curvature выполняет следующие действия:

  • Если есть грунтовая, гравийная, грязная и т.п. метка поверхности, отфильтровать дорогу.
  • Если имеется тег мощеной, асфальтовой или бетонной поверхности, включите дорогу и сделайте ее толстой и непрозрачной.
  • Если дорога является основной, второстепенной, магистралей или автомагистралью, включите ее и сделайте ее толстой и непрозрачной.
  • Если дорога относится к более низкой классификации и нет тега поверхности, включите его, но сделайте его тонким и полупрозрачным.

Стилизация дорог с неизвестным покрытием как менее непрозрачных обеспечивает визуальную индикацию того, что эти дороги могут быть грунтовыми. Увеличение спутниковых изображений может быть полезно для проверки дорожного покрытия, пока вы находитесь дома, вместо того, чтобы путешествовать часами только для того, чтобы обнаружить, что ваша эпическая дорога на самом деле представляет собой грунтовую лесовозную колею. Когда вы идентифицируете грунтовые дороги, вы можете редактировать их теги поверхности в OpenStreetMap, чтобы улучшить данные для всех.

Кривизна бега

Если вам нужны только результаты, я предоставлю веб-карту по адресу roadcurvature.com/map/ и бесплатно загружу выходные файлы Curvature для всего мира на kml.roadcurvature.com. Карта и загрузки автоматически обновляются примерно каждый месяц. Тем не менее, некоторые люди могут захотеть запустить Curvature самостоятельно, чтобы настроить вывод в соответствии со своими потребностями.

При запуске Curvature вы можете создавать пользовательские цепочки обработки (как описано в README), которые позволяют вам выделять дороги, которые вас больше всего интересуют. Например, если вы живете на плоском Среднем Западе, вы можете пройти его с низкой оценкой Порог кривизны , чтобы попытаться найти дороги, которые имеют любых кривых. Дайте ему средний порог, и результаты помогут вам найти более интересный маршрут для работы. Точно так же, если вы хотите найти только самые сумасшедшие извилистые дороги в регионе, установите для него высокий порог, чтобы отфильтровать пшеницу от плевел.

При выводе curvature-output-kml-curve-radius файлы KML будут генерироваться с цветовой кодировкой каждого сегмента дороги в соответствии с его радиусом кривой. Зеленые сегменты находятся выше порога, считающегося «прямым», тогда как желтые — это широкие кривые, оранжевые — средние, а красные — самые узкие:

Этот вывод особенно полезен для проверки вывода программы и поиска фиктивных поворотов, вызванных дрожащими дорожными данными.

7.4: Горизонтальные кривые — Инженерные тексты LibreTexts

  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    47345
    • David Levinson et al.
    • Ассоциированный профессор (инженерия) через Википедию

    Горизонтальные кривые являются одним из двух важных переходных элементов в геометрическом проектировании автомобильных дорог (наряду с вертикальными кривыми). Горизонтальная кривая обеспечивает переход между двумя касательными полосами проезжей части, позволяя транспортному средству проходить поворот постепенно, а не резко. Дизайн кривой зависит от предполагаемой расчетной скорости проезжей части, а также от других факторов, включая дренаж и трение. Эти кривые представляют собой полукруги, чтобы обеспечить водителю постоянную скорость поворота с радиусами, определяемыми законами физики, окружающей центростремительную силу.

    Основные свойства горизонтальной кривой

    Горизонтальная кривая в Осло, Норвегия

    Физические свойства

    Помимо импульса, когда транспортное средство совершает поворот, на него действуют две силы. Во-первых, это гравитация, которая притягивает транспортное средство к земле. Вторая — центробежная сила, для которой требуется противоположное центростремительное ускорение, чтобы удерживать транспортное средство на криволинейной траектории. Для любой заданной скорости центростремительная сила должна быть больше для более крутого поворота (с меньшим радиусом), чем для более широкого (с большим радиусом). На ровной поверхности боковое трение \(f_s\) служит противодействующей силой центробежной силе, но обычно оно оказывает очень небольшое сопротивление/силу. Таким образом, транспортное средство должно сделать очень широкий круг, чтобы сделать поворот на уровне.

    Учитывая, что конструкция дорог обычно ограничена очень узкими проектными зонами, широкие повороты, как правило, не рекомендуются. Чтобы решить эту проблему, проектировщики горизонтальных кривых включают дороги, наклоненные под небольшим углом. Этот наклон определяется как вираж, или \(e\), который представляет собой величину подъема, видимого на наклонном поперечном сечении дороги при определенном пробеге, также известном как уклон. Наличие виража на кривой позволяет частично противодействовать центростремительной силе земли, что позволяет выполнять поворот с большей скоростью, чем это было бы разрешено на плоской поверхности. Вираж также играет еще одну важную роль, способствуя дренажу во время осадков, поскольку вода стекает с дороги, а не собирается на ней. Как правило, вираж ограничивается значением менее 14 процентов, поскольку инженерам необходимо учитывать остановившиеся транспортные средства на кривой, где центростремительная сила отсутствует. 92}{g(e+f_s)}\]

    С помощью этого радиуса врачи-практики могут определить степень искривления, чтобы увидеть, соответствует ли она приемлемым стандартам. Степень кривой, \(D_a\), можно вычислить по следующей формуле, которая приведена в метрике.

    \[%R=\frac{1746}{D_a}%\]

    Где:

    • \(D_a\)= степень изгиба [угол, образуемый дугой длиной 30,5 м (100 футов) вдоль горизонтали кривая

    Применение виража Bristol Motor Speedway

    Одно место, где вы увидите крутые виражи, это автомобильные ипподромы. Эти трассы не работают зимой, поэтому можно избежать проблем с креном в зимнюю погоду. Водители также отличаются особой квалификацией, хотя аварии нередки. Для поклонников NASCAR может быть интересна следующая таблица.

    Таблица: Банковские услуги на ипподромах США

    Трек Длина (мили) Банковское дело (градусы)
    Чикаго Мотор Спидвей 1 0,00
    Гоночная трасса Infineon 1,949
    Уоткинс Глен Интернэшнл 2,45
    Гоночная трасса Поконо 2,5 6,00
    Хомстед-Майами Спидвей 1,5 8.00
    Индианаполис Мотор Спидвей 2,5 9. 00
    Парк Мемфиса Моторспортс 0,75 11.00
    Международная гоночная трасса Феникс 1 11.00
    Лас-Вегас Мотор Спидвей 1,5 12.00
    Мартинсвилл Спидвей 0,526 12.00
    Международная гоночная трасса Нью-Гэмпшира 1.058 12.00
    Калифорния Спидвей 2 14.00
    Кентукки Спидвей 1,5 14.00
    Международная гоночная трасса Ричмонда 0,75 14.00
    Канзас Спидвей 1,5 15. 00
    Международная гоночная трасса Мичигана 2 18.00
    Нэшвилл Спидвей США 0,596 18.00
    Спидвей Северной Каролины 1.017 22.00
    Гоночная трасса Дарлингтона 1,366 23.00
    Атланта Мотор Спидвей 1,54 24.00
    Международная гоночная трасса Довер-Даунс 1 24.00
    Автодром Лоу 1,5 24.00
    Техас Мотор Спидвей 1,5 24.00
    Международная гоночная трасса Дайтона 2,5 31. 00
    Талладега Суперспидвей 2,66 33,00
    Бристоль Мотор Спидвей 0,533 36.00

    Геометрические свойства

    Горизонтальные кривые возникают в местах пересечения двух дорог, обеспечивая постепенный переход между ними. Точка пересечения двух дорог определяется как точка пересечения тангенса (PI) . Местоположение начальной точки кривой определяется как Point of Curve (PC) , а положение конечной точки кривой определяется как Точка касательной (PT) . PC — это расстояние \(T\) от PI, где \(T\) определяется как длина касательной. Длину касательной можно рассчитать, найдя центральный угол кривой в градусах. Этот угол равен сумме внутреннего угла между двумя касательными к дороге.

    Типичная горизонтальная кривая (вид в плане)

    \[T=Rtan \left( \frac{\Delta}{2} \right)\]

    Где:

    • \(T\)= длина касательной (в длине ед. )
    • \(\Delta\)= центральный угол кривой, в градусах
    • \(R\)= радиус кривой (в единицах длины)

    PT — это расстояние \(L\) от PC, где \(L\) определяется как длина кривой. Длину кривой можно определить по формуле для длины полуокружности:

    \[L=\frac{R \Delta \pi}{180}\]

    Расстояние между PI и вершиной кривой можно легко рассчитать по формуле используя свойство прямоугольных треугольников с \(T\) и \(R\). Взяв это расстояние и вычтя радиус кривой \(R\), можно найти внешнее расстояние \(E\), которое является наименьшим расстоянием между кривой и PI.

    \[E=R \left( \frac{1}{cos(\frac{\Delta}{2})}-1 \right)\]

    Где:

    • \(E\)= внешний расстояние (в единицах длины)

    Аналогичным образом можно найти среднюю ординату \(M\). Средняя ордината — это максимальное расстояние между линией, проведенной между PC и PT, и кривой. Он падает вдоль линии между вершиной кривой и ТП.

    \[M=R \left(1-cos \left(\frac{\Delta}{2} \right) \right)\]

    Где:

    • \(M\)= средняя ордината (в единицы длины)

    Точно так же геометрическая формула для длины хорды может найти \(C\), которая представляет собой длину хорды для этой кривой.

    \[C=2Rsin \left( \frac{\Delta}{2} \right)\]

    Свойства расстояния видимости Ограниченное расстояние обзора по кривой впереди

    В отличие от прямых, ровных дорог, которые имеют четкую линию видеть на большом расстоянии, горизонтальные кривые представляют собой уникальную проблему. Естественный ландшафт внутри кривой, такой как деревья, скалы или здания, потенциально может блокировать обзор водителю предстоящей дороги, если он расположен слишком близко к дороге. В результате приемлемая расчетная скорость часто снижается из-за ограничений по дальности видимости.

    Существует два сценария расчета приемлемого расстояния видимости для заданной кривой. Во-первых, расстояние видимости меньше длины кривой. Во-вторых, когда расстояние видимости превышает длину кривой. Каждый сценарий имеет соответствующую формулу, которая определяет расстояние видимости на основе геометрических свойств. Определение того, какой сценарий является правильным, часто требует тестирования обоих, чтобы выяснить, какой из них верен.

    При определенном расстоянии видимости \(S\) и известной длине кривой \(L\) и радиусе осевой линии внутренней полосы движения \(R_v\) расстояние, на котором может находиться препятствие видимости от внутреннего края дороги, \( M_s\) можно вычислить по следующим формулам.

    \[S

    \[S>L:M_s=R_v \left( 1-cos\frac {28.65L}{R_v} \right)+\left( \frac{S-L}{2} \right)sin \left(\frac{28.56L}{R_v} \right)\]

    Демонстрации

    • Flash анимация: Roadside Clear Zone (Карен Диксон и Томас Уолл)
    • Флэш-анимация: Вираж (Карен Диксон и Томас Уолл)

    Примеры

    Пример 1: Радиус кривой

    Извилистая дорога имеет расчетную скорость 110 км/ч. На одной горизонтальной кривой вираж установлен равным 6,0%, а коэффициент бокового трения равен 0,10. Определить минимальный радиус кривой, обеспечивающий безопасную эксплуатацию автомобиля. 92}{9,8(0,06+0,10)}=595 /text{ } метров\)

    Пример 2. Определение пикетажа

    Горизонтальная кривая спроектирована с радиусом 600 м и, как известно, имеет длину касательной 52 м. . PI находится на станции 200+00. Определить местонахождение ПТ.

    Решение

    Что известно об этой проблеме

    \(T=Rtan \left(\frac{\Delta}{2} \right)\)

    \(52=600tan \left(\frac{\Delta}{2} \right)\)

    \ (\Delta=9.9 \text{ } град\)

    \(L=\frac{R \pi \Delta}{180}=\frac{600 \pi 9.9}{180}=104\)

    \(ПК=PI-T=200+00-0+52=199+48\)

    \(PT=ПК+L=199+48+1+04 =200+52\)

    Пример 3: Тормозной путь

    Очень длинный горизонтальный поворот на однонаправленной гоночной трассе имеет радиус центральной линии 1750 метров, две полосы шириной 4 метра и расчетную скорость 200 км/ч. Определите ближайшее расстояние от внутреннего края трассы, на котором зрители могут припарковаться, не мешая водителям на необходимом расстоянии обзора. Предположим, что расстояние видимости меньше длины кривой, коэффициент трения равен 0,3, а время восприятия-реакции равно 2,5 секунды.

    Решение

    При радиусе осевой линии 1750 метров осевая линия внутренней полосы находится на расстоянии 1748 метров от вершины (1750 — (4/2)). Используя формулу расстояния видимости при остановке (см. Расстояние видимости), SSD вычисляется равным 664 метрам. При этом можно легко определить расстояние от трассы, на котором могут парковаться зрители.

    \(S

    Указывает расстояние (31,43 м) до центра внутренней полосы движения. Вычитание половины ширины полосы движения (в данном случае 2 м) дает расстояние до края дорожки, равное 29,43 м.

    Пример задачи

    Данная кривая была построена очень плохо. Используемая двухполосная дорога имеет коэффициент трения ниже среднего (0,05), отсутствие виража и ширину полосы движения 4 метра. 900-килограммовые автомобили имеют тенденцию двигаться по этой кривой и стилистически являются очень тяжелыми. Инженеры округа предупредили, что этот поворот не может быть пройден так же безопасно, как другие повороты в этом районе, но политики хотят сохранить скорость, чтобы стимулировать туризм в этом районе. Кривые имеют радиус 500 футов и расчетную скорость 80 км/ч. Поскольку транспортные средства, использующие кривую, очень тяжелые, они имеют тенденцию переворачиваться, если на них действует слишком большая боковая сила (местные дети часто мчатся по кривой ночью, чтобы получить острые ощущения от «двухколесного»). Как инженер, вы должны доказать, что эта кривая невозможна, прежде чем произойдет авария. Как вы можете показать это? 92}{9,8(0,05+0)=500-(4/2)\)

    \(v=15,62 \text{ } м/с=56,23 \text{ } км/ч\)

    80 км/ч намного больше, чем 56,23 км/ч, что по умолчанию означает, что на автомобиль действует больше силы, чем может противостоять дорога. Таким образом, ограничение скорости на кривой опасно и должно быть изменено.

    Демонстрации

    Дополнительные вопросы

    Домашнее задание

    1. Почему максимальный вираж может быть выше в Южном Техасе, чем в Северной Миннесоте?

    2. Какое коническое сечение лежит в основе горизонтальных кривых?

    3. Когда транспортное средство движется по горизонтальной кривой, на него действуют две силы. Что это за силы и как они действуют на транспортное средство (нарисуйте четкую схему, иллюстрирующую силы).

    4. Существующая горизонтальная кривая имеет радиус 100 метров, что ограничивает максимальную скорость на этом участке дороги. Дорожные службы хотят, чтобы максимальная расчетная скорость составляла 150 км/ч.

    Предположим, что коэффициент бокового трения равен 0,15, а скорость виража как на исходной, так и на восстановленной секции равна 0,06.

    Вычислите существующую скорость и найдите новый радиус кривизны.

    5. Плоская горизонтальная кривая на 2-х полосной магистрали спроектирована с радиусом 609,600 м, кривая имеет длину касательной 121,920 м и PI находится на станции 3+139,440

    Расчетная скорость (км /ч) Расстояние реакции тормоза (м) Тормозной путь на уровне (м) Расчетная дистанция видимости для остановки (м) Расчетное расстояние видимости для остановки (м)
    80 55,2 73,4 129,0 130
    90 62,6 92,9 155,5 160
    100 69,5 114,7 184,2 185
    110 76,5 138,8 215,3 220

    Источник: AASHTO: Политика геометрического проектирования автомагистралей и улиц

    Дорога имеет 3,6 м полосы движения и расчетную скорость 96 км/ч.

    а. Определить местонахождение ПТ. Нарисуйте свое решение. б. Определите расстояние, которое необходимо преодолеть от внутреннего края внутренней полосы движения, чтобы обеспечить достаточную дистанцию ​​видимости для остановки. Нарисуйте свое решение.

    6. Горизонтальная кривая спроектирована радиусом 600 м. Кривая имеет касательную 125 м, а PI находится на метрической станции 10+000 (10 километров и 0 метров). Определить местонахождение ПТ. Нарисуйте схему, показывающую ваш ответ.

    Дополнительные вопросы

    1. Назовите 4 типа горизонтальных кривых.
    2. Когда чаще всего используются непростые типы? Почему обратные кривые так плохи? → Особые условия, включая горы, ограниченное право проезда или любое другое место, где невозможно использовать простой поворот.
    3. Как учитывается погода (например, лед) → вираж (e)
    4. Объясни м? Когда m и M будут равны? Используются ли уравнения для «m» при определении размещения зданий или рекламных щитов на существующих дорогах? → Используется в качестве оправдания, чтобы держать вещи подальше от дороги. Может использоваться при строительстве дорог, чтобы избежать неподвижных объектов, или при размещении объектов, чтобы избежать неподвижной дороги.
    5. Когда следует проектировать скорость для кривых, а не кривую для скорости? → Если это новая конструкция, спроектируйте радиус таким образом, чтобы обеспечить желаемую скорость. Если вы устанавливаете ограничения скорости, установите скорость на основе существующей кривой.
    6. При увеличении угла увеличивается или уменьшается длина касательной
    7. Написать ограничения на расчет горизонтальных кривых
    8. Каковы характеристики горизонтальных кривых
    9. Нарисуйте простую горизонтальную кривую и ее компоненты.
    10. Можно ли добавить T к станции PI, чтобы получить станцию ​​ПК? (№)
    11. Насколько распространена горизонтальная кривая на вертикальной кривой? → Зависит от того, где вы находитесь, очень часто встречается в горных районах. Не особенно редко.
    12. Большинство горизонтальных кривых построены с использованием кругов? → (В США почти равномерно да. Так же проще водителю, которому нужно только выставить руль, не требуется постоянная подрегулировка)
    13. Что в английских единицах означает станция 10+25? Это указывает на то, что станция находится на расстоянии 1025 футов от 0+00.
    14. На бетонных дорогах имеются канавки, перпендикулярные направлению движения, для увеличения трения при торможении. Снижают ли эти канавки боковое трение?
    15. Какой максимальный вираж, когда дорога действительно гололедица? → вираж не может меняться в зависимости от сезона (домкратить дорогу будет слишком дорого). Таким образом, Max \(e\) является годовым.
    16. Почему коэффициенты бокового трения для городских и сельских дорог различаются? Чем отличаются сельские и городские районы?
    17. Почему радиус кривизны важен при строительстве дорог?
    18. Каковы самые высокие значения e и \(f_s\) в стране?
    19. Почему стандарты (максимумы/минимумы) для e и \(f_s\) меняются в зависимости от местоположения?
    20. Обозначьте все силы, действующие на транспортное средство, движущееся в гору (и за угол)
    21. Что такое сопротивление кривой? Что влияет есть? Почему это имеет значение?
    22. Какие основные переменные используются в задачах кривизны, виража?
    23. Почему инженеры делают кривые?
    24. Что такое центробежная сила?
    25. Зачем инженеру увеличивать или уменьшать радиус кривизны?
    26. Что представляет собой вираж
    27. Какие формы имеют горизонтальные и вертикальные кривые. Почему это полезно для драйвера
    28. Если вы хотите уменьшить \(R,\), какие у вас есть стратегии?
    29. Является ли боковое трение таким же, как трение покоя? Что это значит?
    30. Когда задано максимальное значение \(e\), можно ли использовать меньшее число в окончательном ответе → да
    31. Что такое вираж? Как на него действует центробежная сила?
    32. Как \(f_s\) влияет на проектные скорости

    Переменные

    • \(R\) — Радиус центральной линии
    • \(D_a\) — Степень кривой [угол, образуемый дугой 30,5 м (100 футов) вдоль горизонтальной кривой
    • \(T\) — длина касательной (в единицах длины)
    • \(\Delta\) — Угол отклонения касательных кривой. Также центральный угол кривой в градусах.
    • \(E\) — Внешний. Наименьшее расстояние между кривой и PI
    • \(M\) — Средняя ордината
    • \(L\) — Длина кривой
    • \(C\) — Длина хорды
    • \(S\) — Расстояние видимости
    • \(M_s\) — Приемлемое расстояние от внутреннего края дороги для размещения препятствия видимости, не мешающего обзору
    • \(R_v\) — Радиус центральной линии самой внутренней полосы движения

    Ключевые термины

    • ПК: точка кривой
    • PI: точка пересечения касательной
    • PT: точка касания

    Эта страница под названием 7. 4: Горизонтальные кривые распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Дэвидом Левинсоном и др. (Википедия) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

    1. Наверх
      • Была ли эта статья полезной?
      1. Тип изделия
        Раздел или страница
        Автор
        Дэвид Левинсон, Генри Лю, Уильям Гаррисон, Марк Хикман, Адам Данчик, Майкл Корбетт, Брендан Ни. Карен Диксон и ее студенты
        Лицензия
        CC BY-SA
        Версия лицензии
        4,0
      2. Метки
        1. source@https://en. wikibooks.org/wiki/Fundamentals_of_Transportation

      ROCA — набор инструментов ArcGIS для определения трассы дорог и расчета радиусов горизонтальных кривых

      PLoS One. 2018; 13(12): e0208407.

      Опубликовано в сети 26 декабря 2018 г. doi: 10.1371/journal.pone.0208407

      , Концептуализация, Исследование, Методология, Управление проектом, Надзор, Проверка, Написание – первоначальный проект, Написание – обзор и редактирование, # * , Методология, Написание – обзор и редактирование, # , Курирование данных, Формальный анализ, Программное обеспечение, Письмо – рецензирование и редактирование, и , Формальный анализ, Программное обеспечение, Письмо – рецензирование и редактирование #

      Чжися Ли, редактор

      Информация об авторе Примечания к статье Информация об авторских правах и лицензии Отказ от ответственности

      Заявление о доступности данных

      Мы представляем программное обеспечение ROCA (Road Curvature Analyst) в форме ESRI ArcGIS Toolbox, предназначенное для обработки векторных линейных данных. Программное обеспечение сегментирует данные дорожной сети на касательные и горизонтальные кривые. Затем автоматически вычисляются горизонтальные радиусы кривых и азимуты касательных. Одновременно рассчитываются дополнительные часто используемые характеристики участка дороги, такие как извилистость участка дороги (коэффициент объезда), количество поворотов на отдельном участке дороги и средний суммарный угол для участка дороги. Идентификация кривых основана на наивном байесовском классификаторе, и пользователям разрешено подготавливать свои собственные файлы обучающих данных. Мы применили программное обеспечение ROCA к второстепенным дорогам чешской дорожной сети (9,980 км). Обработка данных заняла менее десяти минут. Приблизительно 43% рассматриваемой дорожной сети состоит из 42 752 горизонтальных поворотов. Программное обеспечение ROCA превосходит другие существующие автоматические методы на 26% по проценту правильно идентифицированных кривых. Сегментированные второстепенные дороги в сети автомобильных дорог Чехии можно просмотреть в приложении веб-карты roca. cdvgis.cz/czechia. Мы объединили данные о геометрии дороги с базой данных дорожно-транспортных происшествий, чтобы разработать коэффициенты модификации аварии для горизонтальных кривых с различными радиусами. Установлено, что горизонтальные кривые радиусом 50 м примерно в 3,7 раза более опасны, чем горизонтальные кривые радиусом 1000 м. Программное обеспечение ROCA можно бесплатно загрузить для некоммерческого использования с веб-сайта https://roca.cdvinfo.cz/.

      Хотя выравнивание дорог используется во многих исследованиях, связанных с безопасностью дорожного движения, информация о том, является ли участок дороги кривой или прямой, часто отсутствует в исходных базах данных дорожной сети. Идентификация горизонтальных кривых по данным дорожной сети по-прежнему является трудоемким и подверженным ошибкам процессом. Более того, при ручном выводе такие работы невозможно воспроизвести в будущем. В настоящее время в ГИС хранится большой объем данных о дорожной сети с достаточной пространственной точностью, позволяющей проводить автоматизированную обработку данных. Таким образом, существует потребность в полностью автоматизированном инструменте для извлечения трассы дорог из цифровых данных (например, [1, 2, 3]).

      Отсутствие данных о выравнивании дорог и необходимость определения геометрии дорог вручную, по всей вероятности, являются причиной относительно небольшого количества отдельных горизонтальных кривых, используемых в большинстве исследований. McBean [4] имел, например, всего 100 горизонтальных кривых при работе с данными из Великобритании, как и Othman при соавт. [5] при изучении характеристик безопасности горизонтальных кривых на основе данных натуралистического вождения. Фитцпатрик и др. [6] работал с 260 кривыми. Fink и Krammes [7] и Persaud et al. [8] использовали большее количество данных, более 500. Напротив, Zegeer et al. [9], Сакшауг [10] и Khan et al. [11] имел более 10 000 кривых. Они получили информацию о геометрии дорог из национальных дорожных баз данных. Большинство национальных дорожных баз данных обычно не содержат такой информации для всей сети.

      Предыдущая работа по автоматизированному распознаванию горизонтальных кривых из цифровых данных

      В настоящее время не существует полностью автоматического инструмента, способного точно идентифицировать горизонтальные кривые и касательные из цифровых векторных данных. Часто используется полуавтоматическая идентификация [12, 13]. Эксперт определяет конечные точки горизонтальной кривой на экране, после чего автоматически вычисляются ее радиус и длина. Однако этот подход не подходит для больших наборов данных. Типичным представителем этих методов является «Калькулятор кривых» [14].

      Xu и Wei [3] представили метод, основанный на вычислении азимута для каждой вершины дороги. Они утверждают, что работа с ГИС является наиболее эффективным способом как с точки зрения времени, так и с экономической точки зрения при анализе больших наборов данных. Ли и др. [1] разработали полностью автоматизированный метод для ГИС, который вычисляет «угол пеленга». Они применили порог при выборе между горизонтальными кривыми и касательными. Ли и др. [1] заявил, что «Помимо этого полуавтоматического подхода , не было найдено литературы, документирующей полностью автоматический метод . Таким образом, , CurveFinder является поистине инновационным и уникальным, предлагая средства для автоматического получения местоположения кривой и геометрической информации из карт дорог ГИС . » Мы представим здесь подход, который превосходит CurveFinder, потому что наш подход использует не только угол пеленга, чтобы решить, принадлежит ли вершина дороги горизонтальной кривой или касательной, но еще пять независимых переменных (EV) геометрии дороги. и процедура классификации вместо простого порога (подробности см. В разделе «Методы» ниже).

      Коэффициенты модификации при столкновении для горизонтальных кривых в различных странах

      Коэффициенты модификации при аварии (CMF) для горизонтальных кривых относятся к наиболее часто применяемым областям, где используется геометрия дорог. Мы выбрали это приложение, чтобы продемонстрировать эффективность программного обеспечения ROCA в исследованиях, связанных с безопасностью дорожного движения.

      Юревич и Пита [15] работали с горизонтальными кривыми, ранее разделенными на три группы. Они пришли к выводу, что если количество аварий на кривых радиусом более 1500 м установить равным 1, соответствующие значения будут 1,422 для кривых радиусом от 600 до 1500 м и 2,437 для кривых радиусом менее 600 м. . Персо и др. [8] использовали данные о горизонтальных кривых радиусом от 87 до 1150 м в своих исследованиях по выявлению опасных кривых автомагистралей. Они нашли 15 наихудших кривых с самым высоким риском на основе вычисления эмпирической байесовской оценки. Элвик [16] представил метаисследование CMF, основанное на данных нескольких ранее опубликованных исследований из разных стран. Интенсивность аварий на кривых по отношению к длине предшествующей касательной также находится в центре внимания исследований (например, [17, 18]), а также различия в частоте аварий между горизонтальными кривыми и касательными (например, [19]). , 20]).

      Целью данной работы является представление программного обеспечения ROCA, способного существенно повысить эффективность исследований, связанных с безопасностью дорожного движения, где требуется информация о геометрии участков дороги.

      Данные

      Участки дорожной сети Чехии были предоставлены Управлением дорог и автомагистралей Чешской Республики в виде пространственных (ГИС) данных. Мы сосредоточились на второстепенных дорогах, которые предназначены для обслуживания различных регионов Чешской Республики. Эксперт вручную определил геометрию дороги для 52 случайно выбранных второстепенных дорог. Мы разделили эти дороги на две группы: обучающий набор, состоящий из 32 дорог (2385 вершин, 68,6 км) и проверочный набор, состоящий из 20 дорог (3360 вершин, 74,1 км).

      Мы также работали с дорожно-транспортными происшествиями, произошедшими на второстепенных дорогах чешской дорожной сети в период 2009–2016 гг. Эти данные взяты из базы данных дорожно-транспортных происшествий Полиции Чешской Республики. По состоянию на 2009 год данные были геолокализованы с помощью GPS. В анализе использовались все дорожно-транспортные происшествия, за исключением перекрестков и улиц в городских районах. Всего мы рассмотрели 56 710 ДТП.

      Методы

      Эта работа основывается на классификационном подходе для эффективной идентификации геометрии дороги, предложенном Андрашиком и Билом [2]. В частности, мы применили ту же идею использования метода классификации для определения горизонтальных кривых и прямых участков дорожной сети, но выбрали другой подход к классификации, позволяющий полностью автоматизировать весь процесс (создание набора инструментов в ArcGIS).

      Дерево классификации [21] было первоначально применено в Andrášik и Bíl [2] как лучший подход среди рассмотренных классификаторов (дерево классификации, нейронная сеть, множественная логистическая регрессия и простой порог для описанных и соприкасающихся кругов в качестве эталона). Подход с использованием дерева классификации имеет несколько преимуществ: простое применение, автоматический выбор соответствующих EV и простая интерпретация [22]. Сообщалось также о недостатках [22], однако наиболее важным из них была общая проблема переобучения, которая требовала дальнейшей обрезки дерева и, таким образом, усложняла весь процесс с точки зрения автоматизированной обработки данных. Поэтому мы заменили метод дерева классификации наивным байесовским классификатором [23]. Наивный байесовский классификатор не страдает от переобучения [24] и хорошо работает даже с очень небольшими обучающими наборами данных [25]. Следовательно, это подходящий подход для автоматизированного использования в нашем программном обеспечении. Кроме того, наивный байесовский классификатор требует мало памяти и времени вычислений [26].

      Наивный байесовский классификатор

      Наивный байесовский классификатор основан на применении теоремы Байеса и предположении о независимости независимых переменных. Хотя это предположение в большинстве случаев нереалистично, как и в нашем случае, производительность наивного байесовского классификатора сравнима с более сложными современными классификаторами [24, 26]. Упомянем лишь основные идеи наивного байесовского классификатора. Теоретические подробности см. в Догерти [23].

      Согласно теореме Байеса выполняется равенство

      P(h.curve|EVs)=f(EVs|h.curve)P(h.curve)Z,

      (1)

      P(тангенс|EVs)=f(EVs|тангенс)P(тангенс )Z,

      (2)

      где f ( EVs | h . кривая ) и f ( EVs | тангенс ) — совместные функции плотности вероятности EVs | ( h . кривая ) и P ( тангенс ) — априорные вероятности наблюдения горизонтальной кривой и касательной соответственно при случайном выборе вершины (точки; набор вершин образует линию в ГИС), а Z — нормировочная константа.

      Априорные вероятности могут быть установлены как равными 0,5, так и в соответствии с относительными частотами вершин, принадлежащих горизонтальным кривым и касательным соответственно. Поскольку нормировочная константа одинакова для обоих P ( h . кривая | ЭВс ) и Р ( тангенс | ЭВс ), нет необходимости его оценивать. Если P ( h . кривая | EVs ) больше, чем P ( тангенс | EVs ), мы классифицируем вершину как принадлежащую горизонтальной кривой. В противном случае вершина классифицируется как принадлежащая касательной.

      Предположение о независимости приводит к следующему упрощению совместных функций плотности вероятности:

      f(EVs|h.curve)=∏i=1nf(EVi|h.curve),

      (3)

      f(EVs|тангенс)=∏i=1nf(EVi|тангенс),

      ( 4)

      где n — общее количество электромобилей.

      Гораздо проще оценить несколько одномерных функций плотности вероятности, чем пытаться оценить совместную функцию плотности вероятности. Кроме того, это позволяет нам избежать проклятия размерности. Эти одномерные функции плотности вероятности должны быть оценены из обучающего набора данных. Джон и Лэнгли [27] продемонстрировали, что производительность наивного байесовского классификатора может быть значительно улучшена за счет использования оценки плотности ядра (непараметрический метод оценки функции плотности вероятности) по сравнению со смешанным допущением нормальности и использованием гауссовских распределений. Поэтому мы применили ядерный подход для оценки одномерных функций плотности вероятности.

      Мы использовали те же шесть EV, что и в Андрашике и Биле [2]:

      • Угол между тремя последовательными точками (иногда называемый «угол азимута» [1],

      • совокупный угол в трех точках ,

      • кумулятивный угол в пяти точках (аналогичная характеристика изменения направления, используемая Xu и Wei [3])

      • радиус описанной окружности,

      • расстояние между двумя последовательными точками.

      Эти электромобили поясняются графически в . См. Andrášik and Bíl [2] для получения подробной информации о расчетах EV. Выбранные EV часто используются для идентификации кривой [28]. В частности, подходящими характеристиками кривизны дороги являются угол между тремя последовательными точками [1], совокупный угол в свободной и пяти точках и радиус описанной окружности [29]. Радиус соприкасающейся окружности также был выбран, поскольку он четко различает горизонтальные кривые и касательные [2]. Мы также рассмотрели расстояния между последовательными точками, чтобы учесть плотность точек.

      Открыть в отдельном окне

      Графическое описание электромобилей.

      Таблица 1

      Описательные данные для идентифицированных горизонтальных кривых.

      Были выбраны два варианта «Максимальный радиус кривой».

      Maximal radius of curve 2100 m 1000 m
      Number of curves 42,752 39,943
      Total length of curves 4,314 km 3,577
      Proportion of the total length of curves 43% 36%
      Number of TCs per kilometer at curves 5. 9 6.1

      Open в отдельном окне

      CMF для горизонтальных кривых

      Мы рассчитали CMF для горизонтальных кривых второстепенных дорог в сети автомобильных дорог Чехии, чтобы продемонстрировать возможности и одно из потенциальных применений программного обеспечения ROCA. Затем дорожно-транспортные происшествия были объединены с ближайшими однородными сегментами дороги для получения основных описательных статистических данных и исходных данных для оценки CMF.

      Мы следовали подходу Persaud et al. [8], который также был применен Элвиком [16] для сравнения CMF, разработанных в разных странах мира. Мы предполагаем, что количество дорожно-транспортных происшествий (ДТП) в пределах горизонтальной кривой зависит от среднегодового суточного трафика (AADT), длины горизонтальной кривой (L [м]), радиуса горизонтальной кривой (R [м] ) и отношение R/L следующим образом:

      Количество ТС в год=eβ1+β2(L/R)AADTβ3Lβ4Rβ5.

      (5)

      Параметры β i , i = 1, …, 5, могут быть подобраны с помощью отрицательно-биномиальной регрессии.

      На следующем шаге мы рассчитали интенсивность аварий (количество ТС в год на миллион километров пути) по горизонтальным кривым с радиусами от R мин = 50 м до R макс

    3. 0
    4. 0
    5. 0
    6. 0
    7. 0 мин. = 1000 м для достижения ЦМП, сравнимой с ЦМП, представленными Элвиком [16]. Поскольку горизонтальная кривая обычно является частью окружности, можно предположить, что длина горизонтальной кривой линейно зависит от ее радиуса, т.е. е. L = ωR , где ω > 0 — угол отклонения в радианах.

      Наконец, мы рассчитали относительную частоту аварий для горизонтальных кривых, установив частоту аварий в горизонтальных кривых с наибольшим радиусом (1000 м) в качестве эталона. Это означает, что относительный коэффициент аварийности для таких кривых равен единице, а остальные коэффициенты аварийности пересчитываются в соответствии с этим перемасштабированием. В заключение, относительная частота аварий зависит только от переменного радиуса горизонтальной кривой:

      Relativecrashrate=(RRmax)(β4−1)β5

      (6)

      Мы также рассчитали дополнительные частые параметры, используемые при оценке участков дорог, такие как коэффициент объезда [30], количество поворотов [31] и средний кумулятивный угол [32].

      Подготовка данных

      Дорожная сеть должна быть разделена на отдельные участки дорог. Пользователи должны сначала проверить качество своей геометрии данных, особенно если существует какая-либо исходная сегментация данных. Это происходит, например, когда дороги пересекают региональные границы. Дополнительные распространенные ошибки данных геометрии линий (пересечение вершин, избыточность вершин) могут исказить классификацию и идентифицированный тип геометрии объекта. Поэтому мы рекомендуем проверять качество входных линейных данных и заранее изменять их форму в панели инструментов Editor или Topology.

      Входные данные

      Помимо входного линейного класса объектов участков дорожной сети, пользователям разрешено вводить предопределенный или собственный текстовый файл (Ввод файла обучающих данных, см. ) с координатами вершин участка дороги и определяемой пользователем геометрической классификацией. . Структура обучающего текстового файла следующая:

      Открыть в отдельном окне

      Среда ROCA в программном обеспечении ArcGIS.

      • ID участка дороги                           #

      • x координата# координаты полилин -вершины

      • Y координата#

      • Классификация геометрии {0,1}# 0 для тангенса и 1 для горизонтальной вклинания

      Пользователи. максимальное значение радиуса, выше которого отрезок считается касательной (Максимальный радиус кривой [м], см. ). Обычно используемые пороговые значения радиуса обычно составляют от 1000 до 2500 м (например, [16]).

      Значение минимально допустимого радиуса горизонтальной кривой (Минимально допустимый радиус кривой [м], см. ), может быть установлено для выявления возможных ошибок во входных данных. Предупреждение с количеством и общей длиной кривых с меньшим радиусом, чем задано здесь, будет показано в итоговом сообщении отчета.

      Мы настоятельно рекомендуем пользователю применить обобщение данных, чтобы отфильтровать возможные ошибки в линейных данных. Можно установить допуск (Допуск обобщения линии [м], см. ). Алгоритм обобщения Дугласа-Пекера встроен в программное обеспечение ROCA для упрощения входных строк и удаления избыточных вершин, которые также могут исказить окончательную классификацию (см. Ресурсы).

      Открыть в отдельном окне

      Примеры ошибок, которые обычно присутствуют в базах данных, содержащих вручную оцифрованные данные.

      Результирующие геометрии ROCA являются гладкими и бесшумными, когда применяется алгоритм обобщения Дугласа-Пекера (с заданным пользователем допуском). Результаты также могут быть неправильно классифицированы в случаях, когда алгоритм обобщения не используется. Цифры обозначают отдельные однородные сегменты дороги.

      Обработка данных

      Общий процесс ROCA описан в . Мы рекомендуем пользователям подготовить свои собственные обучающие наборы данных (шаг 1), в противном случае будет использоваться обучающий набор по умолчанию (основанный на второстепенных дорогах чешской дорожной сети). Затем набор обучающих данных обобщается (шаг 2) и для каждой вершины вычисляются шесть EV (дополнительную информацию см. в разделе «Методы»). Алгоритм обучения (этап 3) применяется для подготовки наивного байесовского классификатора для всего набора данных (этап 4). Выполняется обобщение, и для всех данных вычисляются EV. Наивный байесовский классификатор затем используется для идентификации кривых и касательных (шаг 7). Метод наименьших квадратов и эвристика применяются для оценки радиусов горизонтальных кривых (шаг 8). Наконец, создается выходной файл, содержащий индивидуальную геометрию трассы дороги (шаг 9).) и три новых поля с атрибутами кривизны добавляются в исходный файл данных линии (шаг 10).

      Выходные данные ROCA

      Основные выходные данные ROCA представляют собой новый класс линейных объектов, содержащий как горизонтальные кривые, так и касательные. Каждый выходной сегмент сохраняется как отдельная геометрия линейного объекта со следующими атрибутами:

      • Идентификатор входного участка линии дорожной сети,

      • тип геометрии ROCA (0 – касательная, 1 – кривая),

      • радиус горизонтальной кривой,

      • X, Y центра горизонтальной кривой,

      • азимут касательной (горизонтальный угол между касательной и направлением на север; измеряется по часовой стрелке),

      • длина геометрии ROCA.

      К исходным входным участкам дорожной сети также добавлены новые атрибуты:

      • коэффициент объезда (извилистость участка дороги) как отношение реального (маршрут сети, длина ломаной) и кратчайшего (евклидова) расстояние между конечными точками участка дороги,

      • количество поворотов на участке дороги,

      • средний суммарный угол поворота на километр участка дороги.

      Итоговый отчет, когда анализ ROCA завершен, записывается в виде сообщения при выполнении окна инструментов анализа ROCA. Он содержит:

      • количество касательных с их общей длиной,

      • количество горизонтальных кривых (с определенными радиусами) с их общей длиной,

      • количество горизонтальных кривых радиусом меньше минимально допустимого радиуса кривой (задается пользователем) и их общая длина; он выделяет возможные ошибки во входной геометрии класса линейных объектов.

      Набор инструментов был запрограммирован на Python 2. 7 и может использоваться в ESRI ArcGIS (10.1–10.5). Установка набора инструментов ROCA не требуется, набор инструментов можно просто добавить в наборы инструментов ArcToolboxes. Наше программное обеспечение можно бесплатно загрузить с веб-сайта roca.cdvinfo.cz для некоммерческого использования.

      Проверка наивного байесовского классификатора

      Мы построили наивный байесовский классификатор на основе нашего обучающего набора, состоящего из 32 второстепенных дорог (2385 вершин, 259 кривых). Сначала мы рассчитали EV для всей обучающей выборки. Затем мы оценили функции плотности вероятности EV отдельно для горизонтальных кривых и для прямых сегментов с использованием оценки плотности ядра. На основе этих функций плотности вероятности можно классифицировать любую новую геометрию дорог (см. раздел Наивный байесовский классификатор).

      Мы оценили производительность программного обеспечения ROCA, используя отдельный проверочный набор, состоящий из 20 второстепенных дорог (3360 вершин). Проверочный набор содержал 220 горизонтальных кривых. Вероятность успеха (доля правильно классифицированных вершин) байесовского классификатора составила 82,4%, что аналогично другим классификаторам, рассмотренным в [2]. Большинство неправильно классифицированных вершин располагались на концах горизонтальных кривых.

      Расдорф и др. [29] оценили вероятность успеха правильного определения горизонтальной кривой в 78% для «Калькулятора кривых», 69% для «Поиска кривых» и 80% для «Расширения кривизны». Наш подход позволил правильно определить 95% горизонтальных кривых из проверочного набора. Поэтому кажется, что наш подход превосходит автоматический «Поиск кривой» на 26%, а полуавтоматический «Калькулятор кривой» и «Расширение кривизны» на 17% и 15% соответственно.

      Пример результатов ROCA

      ROCA был применен к второстепенным дорогам в сети автомобильных дорог Чехии (9 980 км), чтобы продемонстрировать свою вычислительную эффективность. Расчет длился менее десяти минут (9мин 45 с) на стандартном ПК (4-ядерный процессор Intel i7-2600 3,4 ГГц, ОЗУ 8 ГБ, Windows 10 Pro 64bit).

      Было установлено, что примерно 43% (4 314 км) второстепенных дорог чешской дорожной сети образованы горизонтальными кривыми. Всего было выявлено 42 752 горизонтальные кривые. Все результаты, включая сегментированную дорожную сеть на однородные сегменты, можно увидеть в приложении веб-карты roca.cdvgis.cz/czechia. Как и следовало ожидать, наиболее частым является радиус 50–200 м. Чуть более 40% горизонтальных поворотов на второстепенных дорогах имеют радиус менее 200 м. Только 2% горизонтальных поворотов на второстепенных дорогах имеют радиус более 1000 м ().

      Открыть в отдельном окне

      Распределение радиусов второстепенных дорог в Чехии.

      За период 2009–2016 гг. зарегистрировано 56 710 дорожно-транспортных происшествий (ДТП), произошедших на второстепенных дорогах. Всего мы рассмотрели 7 911 участков дорог. На 18,1 % участков дорог (6,3 % дорожной сети) ДТП не было. Выяснилось, что 45,2% ТЦ приходится на горизонтальные кривые (см. их распределение по радиусу горизонтальной кривой). Дополнительная информация о полученных результатах представлена ​​в .

      Открыть в отдельном окне

      ВК, возникшие на горизонтальных кривых, и суммарные длины горизонтальных кривых по отношению к радиусу горизонтальной кривой.

      Коэффициент объезда и средний кумулятивный угол поворота на километр рассчитывались для каждого участка дороги как выходные данные программного обеспечения ROCA. Коэффициент объезда варьируется от 1,0 (для участка дороги без горизонтальной кривой) до 6,0. Приблизительно 99% участков дорог имеют коэффициент объезда ниже 1,6 (см. ). Средний кумулятивный угол колеблется от 0 до 5044 градусов на километр с 95% значений ниже 642 градусов на километр (см. ). Среднее значение и медиана среднего суммарного угла составляют 224 и 94 градуса на километр соответственно.

      Открыть в отдельном окне

      Распределения коэффициента объезда (слева) и среднего суммарного угла поворота на километр (справа).

      CMF для горизонтальных кривых в Чешской Республике

      После определения геометрии второстепенных дорог в сети автомобильных дорог Чехии мы разработали CMF для горизонтальных кривых. Во-первых, мы подогнали модель (5) с помощью отрицательно-биномиальной регрессии. Коэффициенты регрессии и их 95% доверительные интервалы приведены в . Затем мы рассчитали относительную частоту аварий по формуле (6).

      Таблица 2

      Коэффициенты регрессии, полученные из отрицательно-биномиальной регрессии, вместе с их 95% доверительными интервалами (в скобках) и среднеквадратической ошибкой прогнозирования (RMSE), оцененной с использованием 10-кратной перекрестной проверки .

      Коэффициент (95% доверительный интервал)
      β 1 -10.1 (-9.9, -10.4)
      β 2 0. 78 (0.92, 0.97)
      β 3 0.88 (0.77, 0.87)
      β 4 -0.15 (-0.21, -0.31)
      β 5 0.32 ( 0,23, 0,40)
      RMSE 1,58

      Открыть в отдельном окне Норвегия (см. ). Обе эти CMF намного более пологие, чем суммарная CMF для восьми стран, разработанная Элвиком [16].

      Открыть в отдельном окне

      CMF радиусов горизонтальных кривых второстепенных дорог в Чехии, Норвегии [10] и средневзвешенное значение для восьми стран, рассчитанное Элвиком [16].

      Представленное программное обеспечение ROCA позволяет быстро обрабатывать данные дорожной сети и идентифицировать прямые и горизонтальные кривые с их радиусами. Он способен значительно сократить время исследований, связанных с безопасностью движения, когда требуется выравнивание дорог. Вся чешская дорожная сеть, разделенная на однородные сегменты, доступна через roca.cdvgis.cz/czechia.

      Программное обеспечение ROCA еще не учитывает переходные (спиральные) кривые, соединяющие касательные и горизонтальные кривые. Основная причина заключается в том, что большинство данных, хранящихся в настоящее время в базах данных, оцифровываются вручную, и поэтому эти сегменты с определенной геометрией обычно не представлены в данных, т.е. их идентификация достаточно сложна.

      Программное обеспечение ROCA позволяет пользователям определять свои собственные наборы данных для тренировок. Эта функция, когда пользователям разрешено определять типы геометрии своими данными, чрезвычайно полезна, так как национальные базы данных были созданы с помощью различных подходов и в различных масштабах (разрешении). Программное обеспечение ROCA можно бесплатно загрузить для некоммерческого использования и исследования с сайта roca.cdvinfo.cz.

      Стоит отметить, что производительность любого программного обеспечения сильно зависит от качества входных данных. Очевидно, что при анализе сильно неточных данных невозможно получить точные результаты (см. также [1]). Поэтому мы рекомендуем пользователям проверять качество исходных данных о дорожной сети до проведения анализа.

      CMF для дорожной сети Чехии

      Мы оценили CMF для второстепенных дорог в чешской дорожной сети, чтобы продемонстрировать потенциал ROCA SW. Горизонтальные кривые с наименьшим радиусом (50 м) примерно в 3,7 раза более опасны, чем кривые с радиусом 1000 м. Результаты, полученные в нашем исследовании, согласуются с выводами, обобщенными Elvik [16], который представил метаисследование CMF на основе данных ранее опубликованных исследований из разных стран. Он приходит к выводу, что «обнаружена тенденция увеличения аварийности по мере уменьшения радиуса кривой» . Это также справедливо для второстепенных дорог в сети дорог Чехии (см. ).

      Статья подготовлена ​​при финансовой поддержке Министерства транспорта в рамках программы долгосрочного концептуального развития научно-исследовательских учреждений по исследовательской инфраструктуре, полученной в рамках Оперативной программы исследований и разработок для инноваций (CZ.1.05/2.1.00/ 03.0064). Спонсоры не участвовали в разработке исследования, сборе и анализе данных, принятии решения о публикации или подготовке рукописи.

      Все данные, необходимые для воспроизведения результатов этого исследования, можно бесплатно загрузить с нашего веб-сайта: https://roca.cdvinfo.cz/downloads/. Мы также включили файл с инструкциями: https://roca.cdvinfo.cz/file/howtoroca/.

      1. Ли З., Читтури М.В., Билл А.Р., Чжэн Д., Нойс Д.А. Автоматизированное извлечение информации о горизонтальных кривых для дорог с малой интенсивностью движения. Протокол транспортных исследований. 2015; 2472: 172–184. [Google Scholar]

      2. Андрашик Р., Бил М. Эффективная идентификация геометрии дороги по цифровым векторным данным. Журнал географических систем. 2016;18(3): 249–264. [Google Scholar]

      3. Xu H, Wei D. Улучшенная идентификация и расчет горизонтальных кривых с помощью слоев дорог географической информационной системы. Протокол транспортных исследований. 2016;2595: 50–58. [Google Scholar]

      4. McBean PA. Влияние геометрии дороги на выборку мест ДТП Отчет лаборатории TRRL 1053. Лаборатория транспортных и дорожных исследований, Кроуторн: 1982. [Google Scholar]

      5. Отман С., Томсон Р., Ланнер Г. Использование данных натуралистических полевых эксплуатационных испытаний для определения горизонтальных кривых. Дж. Трансп. англ. 2012;138(9): 1151–1160. [Google Scholar]

      6. Фитцпатрик К.П.И., Лорд Д., Парк Б.Дж. Коэффициент модификации дорожно-транспортного происшествия на горизонтальной кривой с учетом плотности проезжей части на сельских четырехполосных автомагистралях в Техасе. Журнал транспортного машиностроения. 2010;136(9): 827–835. [Google Scholar]

      7. Финк К.Л., Краммес Р.А. Влияние длины касательной и расстояния видимости на уровень аварийности на горизонтальных поворотах на сельских двухполосных дорогах. Протокол транспортных исследований. 1995; 1500: 162–167. [Академия Google]

      8. Персо Б., Реттинг Р., Лайон С. Рекомендации по идентификации опасных поворотов автомагистралей. Протокол транспортных исследований. 2000; 1717: 14–18. [Google Scholar]

      9. Zegeer CV, Stewart RJ, Council FM, Reinfurt DW, Hamilton E. Влияние геометрических улучшений на горизонтальные кривые на безопасность. Протокол транспортных исследований. 1992; 1356: 11–19. [Google Scholar]. Нота от 2.11.1998. SINTEF, Bygg og miljøteknikk, Тронхейм.

      11. Хан Г., Билл А., Читтури М., Нойс Д.А. Оценка безопасности горизонтальных кривых на сельских неразделенных дорогах. Протокол транспортных исследований. 2014; 2386: 147–157. [Google Scholar]

      12. Богенрайф С., Сулейретт Р. Р., Ханс З. Определение и измерение горизонтальных кривых и их влияние на безопасность дорожного движения. Журнал транспортной безопасности и Безопасность. 2012;4(3): 179–192. [Google Scholar]

      13. Финдли Д., Хаммер Дж. Э., Расдорф В., Зегер К. В., Фаулер Т. Дж. Моделирование влияния пространственных отношений на безопасность горизонтальной кривой. Анализ и предотвращение несчастных случаев. 2012;45:296–304. 10.1016/j.aap.2011.07.018 [PubMed] [CrossRef] [Google Scholar]

      14. ESRI. ArcGIS Desktop: выпуск 10.2 Redlands. Научно-исследовательский институт экологических систем, Калифорния. 2013.

      15. Jurewicz C, Pyta V. Влияние ширины свободной зоны на результаты аварий при съезде с дороги. В: Материалы Австралазийской конференции по исследованию безопасности дорожного движения, охране правопорядка и образованию, 31 августа — 3 сентября 2010 г., Канберра, Австралия.

      16. Элвик Р. Международная переносимость функций модификации аварии для горизонтальных кривых. Анализ и предотвращение несчастных случаев. 2013;59: 487–496. 10.1016/j.aap.2013.07.010 [PubMed] [CrossRef] [Google Scholar]

      17. Хауэр Э. Безопасность и выбор степени искривления. Протокол транспортных исследований. 1999; 1665: 22–27. [Google Scholar]

      18. Findley DJ, Zegeer CV, Sundstrom CA, Hummer JE, Rasdorf W, Fowler TJ. Поиск и измерение горизонтальных кривых в большой сети автомагистралей: подход ГИС. Политика управления общественными работами. 2012;17(2): 189–211. [Google Scholar]

      19. Johnston IR. Изменение поведения водителя на поворотах сельских дорог: обзор недавних исследований. В проц. 11-я конференция Австралийского совета по дорожным исследованиям (ARRB), ARRB Group Limited. 1982;11: 115–124.

      20. Кардосо Х.Л. Оценка безопасности при проектировании и реконструкции горизонтальных кривых. В: Доклад, представленный на 3-м Международном симпозиуме по геометрическому проектированию шоссе, 29 июня — 1 июля 2005 г., Чикаго.

      21. Тан П.Н., Штайнбах М., Кумар В. Введение в интеллектуальный анализ данных Эддисон-Уэсли, США: 2005. [Google Scholar]

      22. Джеймс Г., Виттен Д. , Хасти Т., Тибширани Р. Введение в статистическое обучение. Спрингер, Нью-Йорк; 2015. [Google Scholar]

      23. Догерти Г. Распознавание образов и классификация: введение. Спрингер, Нью-Йорк: 2013. [Google Академия]

      24. Фридман Н. О предвзятости, дисперсии, 0/1-потере и проклятии размерности. Интеллектуальный анализ данных и обнаружение знаний. 1997; 1: 55–77. [Google Scholar]

      25. Форман Г., Коэн И. Обучение на малом: сравнение классификаторов после небольшого обучения. В: Булико Дж. Ф., Эспозито Ф., Джаннотти Ф., Педрески Д. (ред.) Обнаружение знаний в базах данных: PKDD 2004. Конспект лекций по информатике. 2004;3202. [Google Scholar]

      26. Домингос П., Паццани М. Об оптимальности простого байесовского классификатора при нулевых потерях, Машинное обучение. 1997;29: 103–130. [Google Scholar]

      27. Джон Г., Лэнгли П. Оценка непрерывных распределений в байесовских классификаторах. Материалы одиннадцатой конференции по неопределенности в искусственном интеллекте. Монреаль, Канада: Морган Кауфманн. 1995: 338–345.

      28. Имран М., Хассан Й., Паттерсон Д. Процедура на основе GPS–ГИС для отслеживания пути транспортного средства на горизонтальной трассе. Компьютерная гражданская инфраструктура Eng. 2006 г.; 21: 383–394. [Google Scholar]

      29. Rasdorf W, Findley DJ, Zegeer CV, Sundstrom CA, Hummer JE. Оценка ГИС-приложений для сбора данных по горизонтальным кривым. Журнал вычислительной техники в гражданском строительстве. 2012;26(2): 191–203. [Google Scholar]

      30. Алиан С., Бейкер RGV, Вуд С. ДТП с участием пострадавших в сельской местности на Кингс-Хайвей: новый подход к исследованиям безопасности дорожного движения. Анализ и предотвращение несчастных случаев. 2016; 95: 8–19. 10.1016/j.aap.2016.06.005 [PubMed] [CrossRef] [Google Scholar]

      31. Ван С., Куддус М., Исон С. Влияние скорости и кривизны дороги на дорожно-транспортные происшествия в Англии. Журнал географии транспорта. 2009; 17: 385–395. [Google Scholar]

      32. Haynes R, Lake IR, Kingham S, Sabel CE, Pearce J, Barnett R. Влияние кривизны дороги на аварии со смертельным исходом в Новой Зеландии. Анализ и предотвращение несчастных случаев. 2008; 40: 843–850. 10.1016/j.aap.2007.090,013 [PubMed] [CrossRef] [Google Scholar]

      curvature.py — найдите самые извилистые дороги вокруг — AdamFranco.com

      Обновление от октября 2020 г.: кривизна теперь доступна в виде карты в браузере.

      Обновление за ноябрь 2016 г.: Новый специализированный сайт Curvature — roadcurvature.com

      Обновление за октябрь 2013 г.: KML-файлы Google Планета Земля, сгенерированные curvature.py, теперь доступны по всему миру.

      Этим летом, когда я начал заниматься мотоциклетным спортом, у меня появилось дополнительное хобби: я изучал карты и путеводители, чтобы найти дороги, по которым было бы весело ездить. Хотя я отлично провел время на грунтовых дорогах через сельскохозяйственные угодья и широкие открытые шоссе, ничто не сравнится с острыми ощущениями от поворотов на извилистой дороге.

      Несмотря на то, что мне удавалось находить дороги по карте (например, Трейси-роуд), одним из недостатков карты являются крутые повороты, на которые можно опереться, разрешение которых, как правило, ниже разрешения многих карт. Атласы и электронные карты, такие как Google Earth, позволяют увеличивать масштаб, но тогда возникает проблема с поиском жемчужин в море данных. Я понял, что мне нужен способ выделить только самые извилистые дороги, чтобы я знал, куда идти дальше.

      Для тех, кто менее знаком с пересечением картографии и программного обеспечения, электронные картографические системы мира (ваш Garmin/TomTom GPS, Google Earth, MapQuest и т. д.) имеют последовательности тысяч координат, которые связаны друг с другом, определяют пути дорог. по поверхности земли.

      Хотя в большинстве этих систем используются проприетарные наборы данных, служба под названием Open Street Map (OSM) представляет собой проект, управляемый сообществом, который каждый может добавлять и редактировать — Википедия для картографических данных. В некоторых частях мира Open Street Map имеет лучшее покрытие, чем любые коммерческие поставщики; в США исходные данные были импортированы из общедоступного набора данных USGS TIGER, а затем были расширены и улучшены сообществом. Я знал, что эти данные были доступны в течение длительного времени, но только на прошлой неделе я понял, что можно будет искать координаты, из которых состоят дороги, для анализа их геометрии, а не только их положения.

      Я могу получить необработанные данные из Open Street Map для каждой дороги, но как определить, какие из них самые извилистые? Вначале я пробовал такие стратегии, как вычисление отношения пройденного расстояния по дороге к расстоянию между начальной и конечной точками. К сожалению, во всех этих методах были ситуации, которые путали алгоритмы (например, кольцевые дороги) или не различали веселые кривые и скучные широкие изменения направления, которые были бы захватывающими только при превышении ограничения скорости. В конце концов я придумал процесс вычисления радиуса кривизны на каждом сегменте каждой дороги, а затем суммирования длины самых извилистых сегментов, чтобы получить общее расстояние, затраченное на поворот. Чем извилистее дорога, тем больше времени уходит на повороты.

      Я вернусь к более подробной информации чуть позже, но в итоге я написал небольшую программу, которая считывает данные Open Street Map и выдает файлы KML (Google Earth), в которых выделяются только извилистые дороги. Эта программа называется curvature.py и доступна на Github здесь: https://github.com/adamfranco/curvature/wiki

      При запуске curvature.py вы можете передавать различные параметры, позволяющие выделить дороги, которые вас больше всего интересуют. Например, если вы живете на плоском Среднем Западе, вы можете пройти порог низкой кривизны, чтобы попытаться найти дороги, которые имеют любые кривых. Дайте ему средний порог, и результаты помогут вам найти более интересный маршрут для работы. Точно так же, если вы хотите найти только самые сумасшедшие извилистые дороги в регионе, установите для него высокий порог, чтобы отфильтровать пшеницу от плевел.

      При использовании параметра --colorize файлы KML будут генерироваться с цветовой кодировкой каждого сегмента дороги в соответствии с его радиусом кривой. Зеленые сегменты находятся выше порога, считающегося «прямым», тогда как желтые — это широкие кривые, оранжевые — более узкие, а красные — самые узкие:

      Подробнее о расчете кривизны

      Каждый путь (дорога) состоит из последовательности точек, определяемых парой значений широты и долготы. Каждая последовательность из трех точек образует треугольник, две стороны которого являются сегментами дороги с гипотенузой между 1-й и 3-й точками. Поскольку у нас есть широта и долгота каждой точки, мы можем легко вычислить расстояния между ними, но выяснить, какова кривизна дороги в этом наборе точек, немного сложно. Поскольку точки расположены неравномерно, угол между тремя точками нам ничего не говорит. Вместо этого мы должны вернуться к геометрическому соотношению, согласно которому для каждого треугольника существует описанная окружность, пересекающая три его точки. Используя уравнения для описанной окружности, мы можем подставить расстояния между тремя точками и получить радиус этой окружности. Радиус этого круга соответствует радиусу кривой дороги в середине трех точек.

      Вот видео, объясняющее процесс:

      Использование Curvature
      На странице Curvature Examples показано несколько примеров и приведены ссылки на файлы KML, которые можно открыть в Google Планета Земля. Если вы хотите просто просмотреть созданные мной KML-файлы кривизны, вы можете найти их по адресу: http://www2.adamfranco.com/curvature/kml/

      Формула радиуса кривизны — Узнайте формулу для радиуса кривизны

      Радиусом кривизны кривой называется любой примерный радиус окружности в любой заданной точке. По мере движения по кривой радиус кривизны изменяется. Формула радиуса кривизны обозначается как «R». Величина, на которую кривая превращается из плоской в ​​кривую и из кривой обратно в прямую, называется кривизной. Это скалярная величина. Радиус кривизны обратно пропорционален кривизне. Радиус кривизны — это не реальная форма или фигура, а воображаемый круг. {2}} |}\) 9{2}} |}\)

      8. где K — кривизна кривой, K = dT/ds, (функция тангенса-вектора)

      R — радиус кривизны

      Разбивайте сложные понятия с помощью простых визуальных средств.

      Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

      Закажите бесплатный пробный урок

      Давайте быстро рассмотрим пару примеров, чтобы лучше понять формулу радиуса кривизны. 9{2}} |}\).

      Различные типы кривых автомагистралей и их значение

      Дом Оборудование Оборудование Артикул Различные типы кривых автомагистралей и их значение

      Кривые шоссе

      Кривая шоссе представляет собой дугу, соединяющую две прямые линии, разделенные некоторым углом, называемым углом отклонения. Эта ситуация возникает, когда трасса проезжей части или железной дороги меняет свое направление из-за неизбежных объектов или условий. В строительстве автомобильных дорог есть два типа кривых: горизонтальная кривая и вертикальная кривая. Кривые отображаются всякий раз, когда дорога меняет свое направление с правого на S (наоборот) или меняет направление с верхнего на нижнее (наоборот). Кривые являются важным элементом в дизайне дорожного покрытия. Для них предусмотрено максимальное ограничение скорости, которое следует соблюдать очень строго. Соблюдение ограничения скорости становится важным, поскольку превышение скорости может привести к тому, что транспортное средство выйдет из-под контроля во время прохождения поворота, и, таким образом, увеличить вероятность несчастных случаев со смертельным исходом. Кроме того, крайне необходимо принять соответствующие меры безопасности на всех горизонтальных и вертикальных поворотах, чтобы сделать дорожную инфраструктуру удобной для пользователей и снизить риск возникновения опасных обстоятельств.

      Важность поворотов на шоссе

      • Если посредине шоссе внезапно появляются препятствия, такие как горы, скалы и т. д., которые невозможно переместить, поэтому для движения вперед к месту назначения предусмотрен плавный поворот .
      • Автомагистрали, как правило, представляют собой прямые дороги большей протяженности, поэтому может быть более высокая вероятность несчастных случаев из-за перерасхода средств или сонливости за рулем.
      • При наличии искривления водитель приходит в сознание и контролирует свою скорость и сонливость во время движения.
      • Сонливость является основной причиной дорожно-транспортных происшествий на автомагистралях. Если на шоссе имеется кривая, водитель становится бдительным и реагирует на кривизну.
      • Изгибы дорог предусмотрены для удобства пассажиров.
      • Постепенное изменение направления или ориентации выравнивания может быть выполнено с помощью кривых.
      • Кривые предусмотрены для облегчения поворота на дороге и колеи

      Различные типы кривых шоссе

      Существует два типа кривых – горизонтальные и вертикальные кривые. Каждая из них имеет различные подкатегории, каждая из которых описана ниже.

      Горизонтальные кривые

      Кривая, расположенная в горизонтальной плоскости земли или земли, называется горизонтальной кривой. Он соединяет две прямые линии, находящиеся на одном уровне, но имеющие разные или одинаковые направления. Существуют различные типы горизонтальных кривых, описание каждого из них приведено ниже.

      Простая круговая кривая

      Это кривая, состоящая из одной дуги с постоянным радиусом, соединяющей две касательные. Это наиболее распространенный тип горизонтальной кривой. Простая дуга, предусмотренная на дороге или железнодорожном полотне для наложения кривой между двумя прямыми линиями, является простой кривой окружности. Чем меньше степень изгиба, тем более пологая кривая и наоборот. Острота простой кривой также определяется радиусом R. Большие радиусы плоские, а малые радиусы острые. Простая кривая обычно представлена ​​длиной ее радиуса или степенью кривой

      Составная кривая

      Это кривая, состоящая из двух или более дуг окружностей последовательно более коротких или длинных радиусов, соединенных по касательной без изменения кривизны и используемая на некоторых железнодорожных путях и автомагистралях в качестве кривой сервитута для обеспечения меньшего резкий переход от касательной к полной кривой или наоборот. Поскольку длины касательных к ним различаются, составные кривые соответствуют топографии намного лучше, чем простые кривые. Эти кривые легко адаптируются к гористой местности или районам, прорезанным большими извилистыми реками. Однако, поскольку составные кривые более опасны, чем простые кривые, их никогда не следует использовать там, где подойдет простая кривая.

      Горизонтальные кривые

      Обратная кривая

      Обратная кривая состоит из двух или более простых кривых, поворачивающихся в противоположных направлениях. Их точки пересечения лежат на противоположных концах общей касательной, а ПТ первой кривой совпадает с ПК второй. Эта точка называется точкой обратной кривизны (PRC). Обратная кривая состоит из двух дуг одинакового или разного радиуса, изгибающихся или изгибающихся в противоположных направлениях с общей касательной на их стыке, причем их центры находятся на противоположных сторонах кривой.

      Кривая перехода пути

      Кривая перехода пути или спиральный сервитут представляет собой математически рассчитанную кривую на участке шоссе, в которой прямой участок превращается в кривую. Он предназначен для предотвращения резких изменений поперечного направления В плоскости (если смотреть сверху) начало перехода горизонтальной кривой находится на бесконечном радиусе, а в конце перехода оно имеет тот же радиус, что и сама кривая и т.д. образует очень широкую спираль. В то же время в вертикальной плоскости внешняя часть кривой постепенно поднимается до тех пор, пока не будет достигнута правильная степень крена.

      Спиральная кривая

      Спиральные кривые обычно используются для постепенного изменения кривизны от прямого участка дороги к изогнутому участку. Они помогают водителю, обеспечивая естественный путь следования. Спиральные кривые также улучшают внешний вид круговых кривых, уменьшая нарушение выравнивания, воспринимаемое водителями. Использование спирали заключается в том, чтобы заставить дорогу или колею следовать той же форме, которую естественно принимает транспортное средство. В автомобиле вы не переходите сразу от движения прямо к полному повороту. Есть переходная зона, где вы медленно поворачиваете руль. На автомагистралях полосы достаточно широкие, чтобы можно было проехать по спирали, просто передвигаясь с одной стороны полосы на другую.

      Вертикальные кривые

      Эти кривые предназначены для изменения уклона дороги и могут быть или не быть симметричными. Они параболические, а не круговые, как горизонтальные кривые. Определение надлежащего уклона и безопасного расстояния видимости является основным критерием проектирования вертикальной кривой, длина гребня вертикальной кривой должна быть достаточной для обеспечения безопасного расстояния видимости при остановке, а на провисающей вертикальной кривой длина важна, поскольку она влияет на такие факторы, как дальность видимости фар, комфорт водителя и требования к дренажу. Есть два типа вертикальных кривых, которые обсуждаются ниже/9.0003

      Кривая впадины/прогиба

      Кривые впадины или кривые впадины представляют собой вертикальные кривые с выпуклостью вниз. В кривых долины центробежная сила будет действовать вниз вместе с весом транспортного средства, и, следовательно, воздействие на транспортное средство будет больше. Это приведет к рывкам автомобиля и причинит дискомфорт пассажирам. Таким образом, наиболее важными конструктивными факторами, учитываемыми в кривых долины, являются безударное движение транспортных средств с расчетной скоростью и наличие тормозной дистанции при свете фар транспортных средств для ночного вождения. Кривая впадины делается полностью переходной путем предоставления двух аналогичных переходных кривых одинаковой длины.

      Вертикальные кривые

      Кривая вершины

      Кривые вершины — это вертикальные кривые с уклоном вверх. Требования к дальности видимости для безопасности наиболее важны на поворотах вершины. На этих кривых должна быть указана тормозная дистанция или абсолютная минимальная дистанция видимости, а там, где обгон не запрещен, по возможности должна быть указана дистанция видимости для обгона или промежуточная дистанция видимости. Когда быстро движущееся транспортное средство движется по кривой вершины, пассажиры испытывают меньше дискомфорта. Это связано с тем, что центробежная сила будет действовать вверх, пока транспортное средство преодолевает кривую вершины, которая противодействует силе тяжести, и, следовательно, часть давления в шинах сбрасывается. Кроме того, если кривая имеет достаточное расстояние видимости, длина будет достаточной, чтобы ослабить удар из-за изменения уклона.

      Заключение

      Кривые играют жизненно важную роль в геометрическом проектировании трасс, поэтому они должны быть правильно спроектированы, чтобы обеспечить безопасность, комфорт и удобство во время движения транспортных средств или поездов по кривым дорогам. Дизайн кривой зависит от предполагаемой расчетной скорости проезжей части, а также от других факторов, включая дренаж и трение.

      Предыдущая статьяРегистрация собственности в Мумбаи снизилась в августе

      Следующая статьяOmaxe Ltd.

      Добавить комментарий

      Ваш адрес email не будет опубликован. Обязательные поля помечены *