Теплоемкость газов: ᐉ Теплоемкость газов

3. Теплоемкость газов

3.1. Основные определения

Теплоемкость – величина, равная отношению сообщаемой телу или отводимой от него теплоты к соответствующему изменению его температуры: ,

где С – теплоемкость; Q – подведенная (или отведенная) теплота; ∆Т – изменение температуры тела.

В теплотехнических расчетах широко используются удельная и молярная теплоемкости.

Массовой теплоемкостью называется отношение теплоемкости тела к его массе: ,

где с – массовая теплоемкость; m – масса тела.

Молярной теплоемкостью называется отношение теплоемкости к количеству вещества: ,

где μc – молярная теплоемкость; n – количество вещества.

Объемной теплоемкостью называется отношение теплоемкости к 1 м³ газа при нормальных условиях: ,

где – объемная теплоемкость; v₀ – объем газа при нормальных условиях.

Между массовой, объемной и мольной теплоемкостями имеется следующая связь:

3.2. Истинная и средняя теплоемкости

Теплоемкости газов и паров являются переменными величинами; для идеальных газов они зависят от их температуры, а для реальных газов и паров также и от их давления. Поэтому различают теплоемкости истинные и средние. Истинной называется теплоемкость при заданной температуре, а средней – среднее значение теплоемкости в заданном интервале температур, в пределах которых производится подвод или отвод теплоты.

В тепловых расчетах пользуются средними теплоемкостями: удельной и молярной. Средняя удельная теплоемкость вещества равна отношению подведенной теплоты к массе вещества и разности температур в конце и в начале подвода теплоты: .

Средняя молярная теплоемкость вещества равна отношению подведенной теплоты к количеству вещества и разности температур в конце и в начале подвода теплоты: .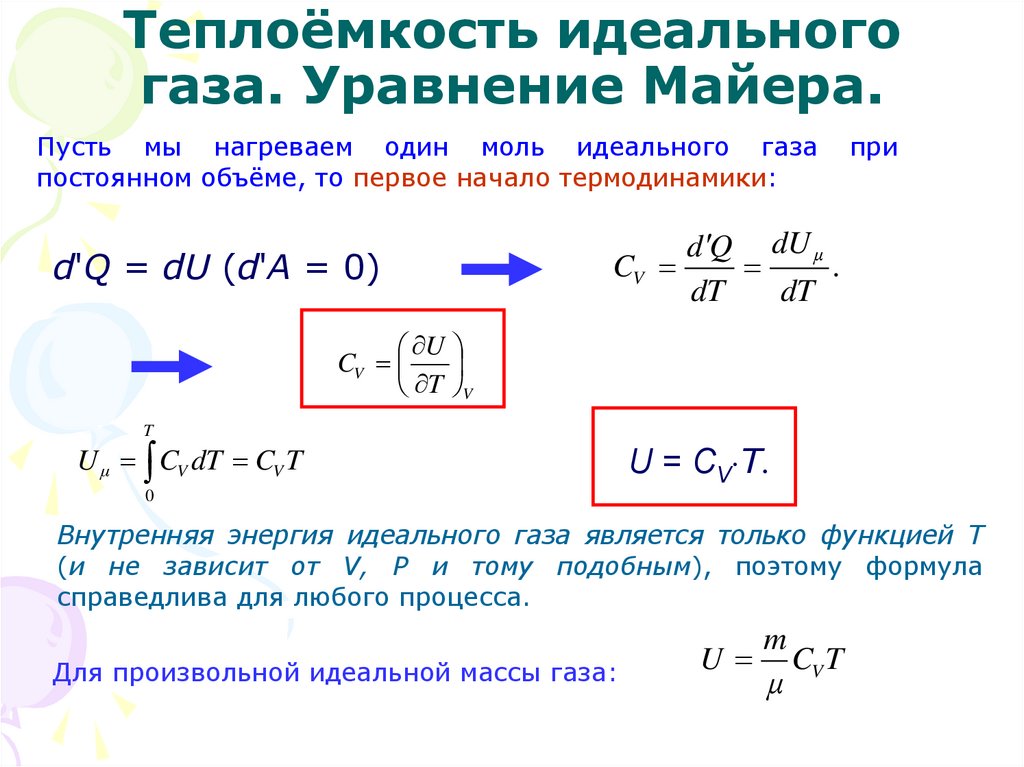

В СИ теплоемкость измеряется , молярная теплоемкость – , объемная теплоемкость с’ – .

3.3. Зависимость теплоемкости от характера процесса

Как было сказано выше, теплоемкость газов в сильной степени зависит от тех условий, при которых происходят процессы их нагревания или охлаждения. Среди этих процессов в технике наиболее важное значение имеют процессы, протекающие при постоянном объеме газа (изохорный процесс) и при постоянном давлении газа (изобарный процесс). В связи с этим различают теплоемкость при постоянном объеме (с_v – массовая изохорная теплоемкость, μс_v– молярная изохорная теплоемкость) и теплоемкость при постоянном давлении (с_p – массовая изобарная теплоемкость, μс_р – молярная изобарная теплоемкость). Количественное соотношение между с_р и с_v устанавливают с помощью уравнения Р. Майера: с

р − с_v= R₀ или μс_р − μс_v= R_μ = 8314,31 , откуда μс_р=μс_v+8314,31 . Таким образом, разность между молярными изобарной и изохорной теплоемкостями для всех газов есть величина постоянная и равна универсальной газовой постоянной.

3.4. Нахождение истинных и средних теплоемкостей

Для нахождения истинной массовой, объемной или молярной теп­лоемкости используют два способа: графический – по c,t–диаграмме и табличный – с использованием специальных таблиц.

В c,t–диаграмме по оси ординат откладываются значения истинной теплоемкости (массовой, объемной или молярной), а по оси абсцисс – температуры.

Пусть истинная удельная теплоемкость на c,t–диаграмме изображается линией 1-2, которая в общем случае являет­ся кривой (рис 3.4.1).

Рис. 3.4.1. Графическое определение средней теплоемкости

в заданном интервале температур

Тогда отрезок 4-1 в масштабе будет истинной удельной теплоемкостью при температуре t_l, a отрезок 3-2 – истинной удель­ной теплоемкостью при темпе­ратуре t₂.

Если заменить площадь 1234 равновеликим ей прямоуголь­ником l’2’З4 с основанием 4–3, то высота его 4–1′ (или 3-2′) и бу­дет представлять в масштабе среднюю удельную теплоем­кость с в процессе 1-2.

Площадь этого прямоуголь­ника равна произведению высо­ты на основание или в данном случае произведению: А = с_m(t₂– t₁).

Умножим пра­вую и левую части уравнения для средней массовой теплоемкости на разность температур (Т

2–Т₁), по­лучим: q_1,2=c_m(Т₂–Т₁)

Сопоставляя правые части последних уравнений, видим, что они равны, поэтому пл. 1234, равнове­ликая пл. 1’2’34, определяет в масштабе удельную подве­денную (или отведенную) теплоту.

Следовательно, на c,t–диаграмме площадь, ограниченная линией истинной удельной теплоемкости, крайними орди­натами этой линии и осью абсцисс, определяет в масштабе удельное количество подведенной или отведенной теплоты.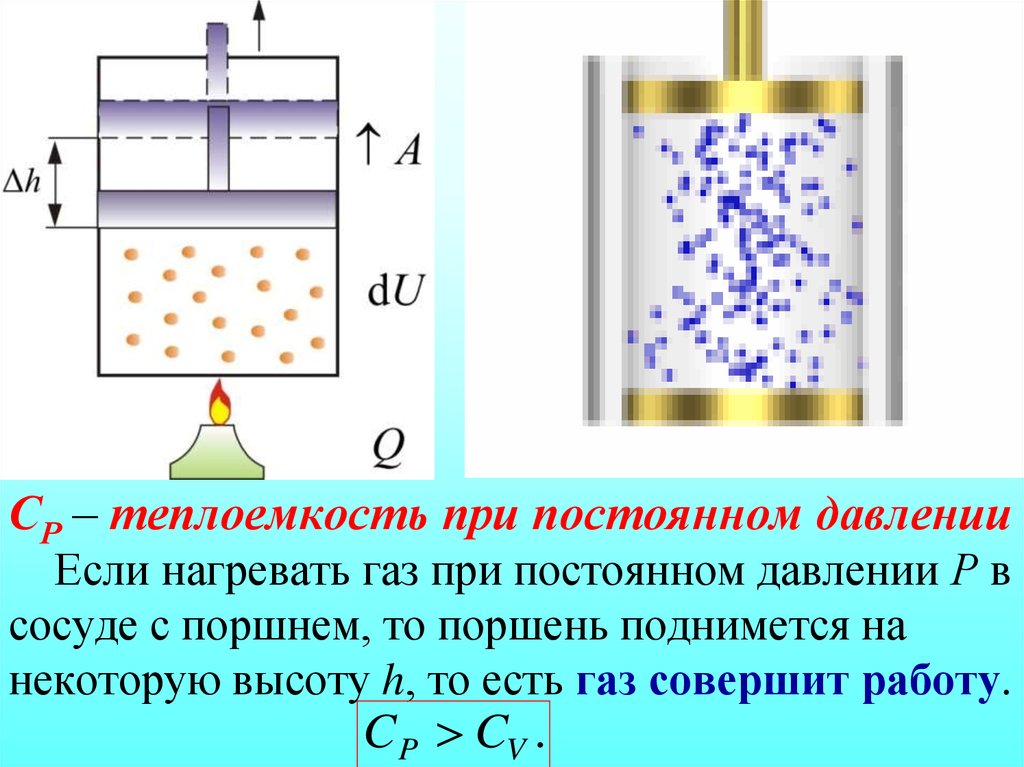

Задача определения средней удельной теплоемкости в заданном процессе значительно упрощается, если линию истинной теплоемкости представить в виде прямой (рис. ).

В этом случае средняя удельная теплоемкость в интер­вале температур t

1–t₂ может быть принята как среднеарифметическая между истинными теплоемкостями с₁ (при темпе­ратуре t₁) и с₂ (при температуре t₂) (рис.3.4.2, а), т. е.

.

Задача нахождения средней удельной теплоемкости (в случае прямолинейной зависимости теплоемкости от темпе­ратуры) может быть еще упрощена, если в качестве ее взять истинную удельную теплоемкость при среднеарифметиче­ской температуре процесса, т.е. при температуре (рис. 3.4.2, б).

Рис. 3.4.2. Определение средней теплоемкости в заданном интервале температур упрощенным способом

Замена криволинейной зависимости теплоемкости от тем­пературы прямолинейной зависимостью вносит некоторую неточность в расчеты, однако незначительную, и поэтому часто ею можно пренебречь.

Нахождение теплоемкостей табличным способом произ­водится с помощью таблиц молярных или удельных теплоемкостей.

В таблице 3 приложения приведены истинные массовые теплоем­кости, часто встречающиеся в тепловых расчетах воздуха и отдельных газов.

Теплоемкость газов | PHYWE

45 Протокол

45 Протокол

Университет

большой сайт

Студенты

Принцип

В сосуд с газом подается тепло при помощи нагревателя, включаемого на непродолжительное время. Рост температуры приводит к повышению давления, измеряемого манометром.

При изобарных условиях повышение температуры приводит к расширению объема, считываемого газовым шприцом. Из изменений объема или давления рассчитываются молярная теплоемкость CV и Cp.

Задание

Определить молярную теплоемкость воздуха при постоянном объеме Cv и постоянном давлении Cp.

Получаем понятие о

уравнении состояния идеального газа 1-м законе термодинамики универсальной газовой постоянной степени свободы молярном объеме изобарах изотермах изохорах и адиабатическом изменении состояния

Наименование

Кат.номер

Количество

Прецизионный манометр

Кат.номер 03091-00

1

Цифровой универсальный счетчик, 4 декады

Кат.номер 13601-99

1

Цифровой мультиметр, 3 1/2 разрядный дисплей с NiCr-Ni термопарой

Кат.номер 07122-00

2

Сосуд Мариотта, 10 л

Кат.номер 02629-00

1

Запорный кран, 1- ходовой, прямой, стеклян.

Кат.номер 36705-00

1

3-ходовой кран, Т-образный, капиллярный, стекло

Кат. номер 36732-00

1

Резиновая пробка, d=32/26 мм, с 3 отверстиями, 7 мм+2х1,5 мм

Кат.номер 39258-14

1

Резиновая пробка, d=59.5/50.5 мм, с 1 отверстием, 7 мм

Кат.номер 39268-01

1

Резиновые трубки, внутренний d=10 мм | :

Кат.номер 39282-00

2

Силиконовые трубки, внутренний d=3 мм | :

Кат.номер 39292-00

1

Никелевый электрод, d=3 мм, с гнездом

Кат.номер 45231-00

2

Хромоникелевая проволока, d=0,1 мм, 100 м

Кат.номер 06109-00

1

Ножницы, прямые, с тупыми концами, l=140 мм

Кат.номер 64625-00

1

Переключатель для 2-х цепей, однополюсный

Кат.номер 06005-00

1

Соединительный проводник, 500 мм, красный | :

Кат.номер 07361-01

4

Соединительный проводник, 500 мм, красный | :

Кат.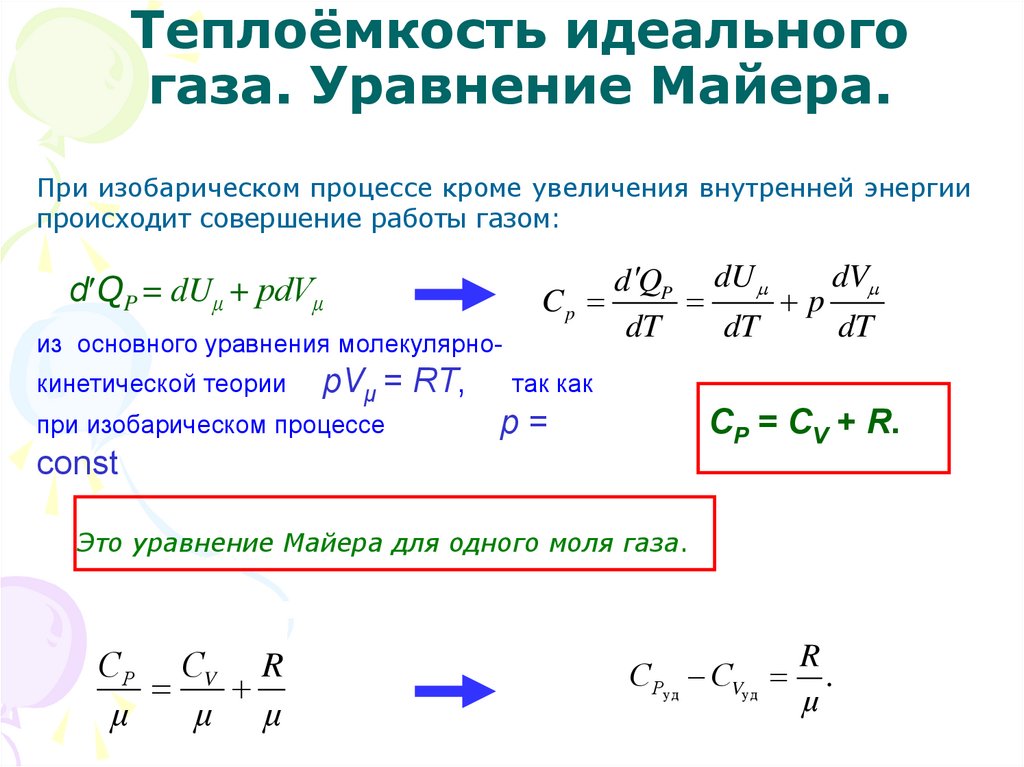 номер 07360-01

1

Соединительный проводник, 500 мм, синий | :

Кат.номер 07361-04

1

Соединительный проводник, 500 мм, синий | :

Кат.номер 07360-04

1

Соединительный проводник, 500 мм, синий | :

Кат.номер 07359-04

2

Шприц,10 мл

Кат.номер 02590-10

1

Переходник для трубок, прямой, d=3-5/6-10мм

Кат.номер 47517-01

1

Электронная погодная метеостанция

Кат.номер 87997-10

1

Треножник

Кат.номер 02002-55

1

Название

Имя файла

Размер файла

Тип файла

(en) Versuchsbeschreibung

p2320201_en .pdf

Размер файла 1.64 Mb

(es) Versuchsbeschreibung

p2320201_es .pdf

Размер файла 1.64 Mb

Бесплатная доставка от 300,- €

Nach oben

Информация

• Контактное лицо
• Условия сотрудничества
• Декларация о конфиденциальности
• Вводные данные

Обслуживание

• Краткий обзор услуг
• Скачать
• Каталоги
• Вебинары и Видео
• Связаться со службой поддержки клиентов

Компания

• О нас
• Качественная политика
• Безопасность в классе

Please note

* Prices subject to VAT.

We only supply companies, institutions and educational facilities. No sales to private individuals.

Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions.

Что такое удельная теплоемкость газов?

Газы выражают свою поглощенную энергию в условиях, когда один грамм газа повышает его температуру на 1 градус Цельсия в виде удельной теплоемкости. Удельная теплоемкость имеет два подкласса, называемых молярной удельной теплоемкостью при постоянном давлении и молярной удельной теплоемкостью при постоянном объеме. Символически они представлены как CP и CV соответственно. Удельная теплоемкость газа может оставаться несколько выше, когда ему позволяют расширяться в результате его нагревания, т. е. представлять как удельную теплоемкость при постоянном давлении по сравнению с тем, когда его нагревают в закрытом сосуде, останавливающем его расширение, что представлена ​​как удельная теплоемкость при постоянном объеме.

Теплоемкость

Теплоемкость просто определяется как количество тепла, необходимое для изменения теплосодержания 1 моля вещества точно на 10°С.

Что такое удельная теплоемкость?

Удельная теплоемкость газа – это количество энергии, необходимое одному грамму газа для повышения температуры на единицу градуса Цельсия. Ее обычно называют теплоемкостью газа, а также молярной теплоемкостью, когда речь идет о молях газа.

Математически удельная теплоемкость представлена ​​как- 

c=CM

Где c = удельная теплоемкость образца, C = теплоемкость вещества и M = масса образца.

 

Теплоемкость является экстенсивным свойством, поскольку зависит от массы вещества. Однако удельная теплоемкость относится к категории интенсивных свойств. Он имеет внутреннюю характеристику, которая не показывает никакой зависимости от размера или формы вещества.

 

Значения удельной теплоемкости можно понимать следующим образом: 

Когда два материала, которые изначально находились при разных температурах, вступают в контакт друг с другом, поток тепла будет направлен от более теплого материала к более холодному.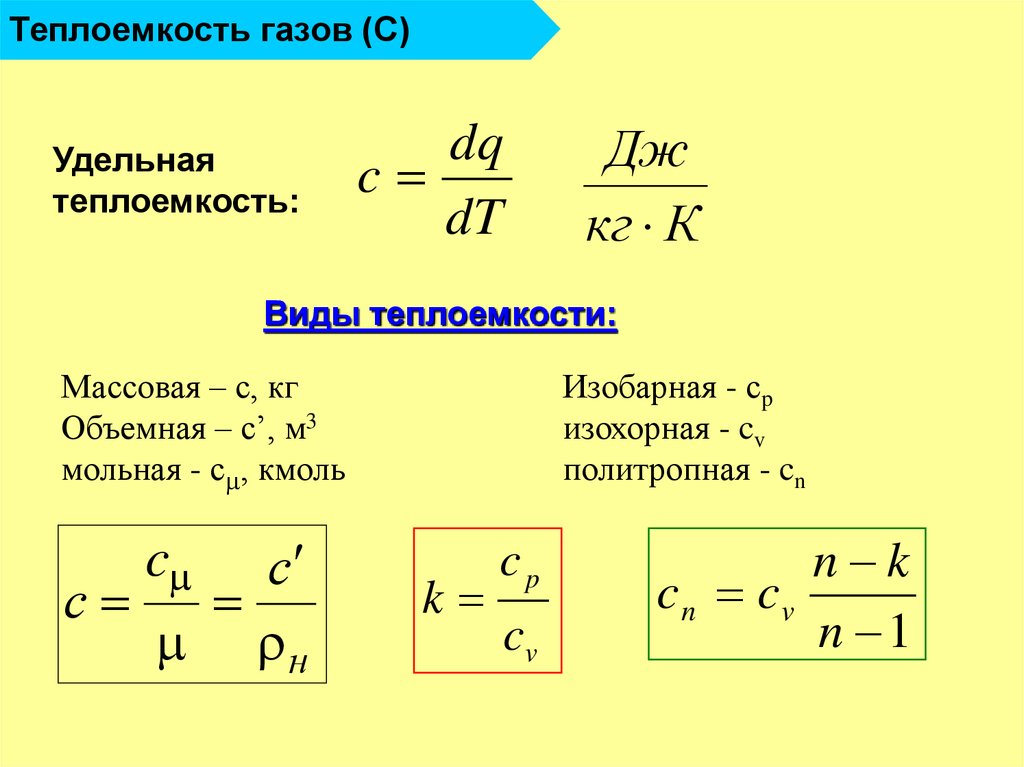 Это будет продолжаться до тех пор, пока оба материала не достигнут одинаковой температуры. Уже понятно, что при поглощении тепловой энергии веществом его температура продолжает увеличиваться. Если одно и то же количество теплоты дается разным веществам, имеющим одинаковую массу, то наблюдается, что повышение температуры для каждого вещества будет различным.

Единица удельной теплоемкости

Единица удельной теплоемкости газов или других веществ в системе СИ определяется как – Джоуль на кельвин на килограмм, т.е. 1моль-1

 

Молярная удельная теплоемкость при постоянном давлении

Молярная удельная теплоемкость при постоянном давлении для идеальных одноатомных газов определяется как количество тепловой энергии, подводимой к образцу, когда он находится при постоянном давлении.

 

Математически это может быть представлено как:

 

CP=52R      – – – – – – (1)

 

Молярная удельная теплоемкость при постоянном объеме

Молярная удельная теплоемкость при постоянном объеме 9000 газов определяется как количество тепловой энергии, подводимой к образцу газов, когда он удерживается при постоянном объеме.

Математически это можно представить как: 

CV=32R       – – – – – – – (2) 

Соотношение между уравнениями (1) и (2):  

CP =CV+R

Однако было замечено, что для многоатомных молекул, относящихся к категории двухатомных или линейных, добавляются две вращательные степени свободы, которые соответствует вращению вокруг двух перпендикулярных осей, проходящих через центр молекулы. Таким образом, можно было бы ожидать, что формула даст CV = 52R, что наблюдается в таких газах, как азот и кислород. Точно так же нелинейные многоатомные молекулы смогут вращаться вокруг трех перпендикулярных осей, что, в свою очередь, изменит формулу на CV=3R

Example of Specific Heat Capacities for Gases

 

Gases	Helium	Argon	Neon	Carbon Dioxide	Метан
С В	79 3. 1036 3 0.3122	0.6179	0.657	1.7354
C P	5.1926	0.5203 ​​	1.0299	0.846	2,2537

Заключение

Удельная теплоемкость газа – это количество энергии в виде теплоты, необходимое единице моля газа для повышения температуры на один градус Цельсия. Он представлен единицей СИ ДжК-1 кг-1 или Дж/(кгК) или ДжК-1моль-1. Далее он делится на два класса по молярной удельной теплоемкости при постоянном давлении и постоянном объеме, представленные C P и C V , соответственно.

Теплоемкость газов

31 мая 2015 г. 30 ноября 2011 г. от Mini Physics

Подводимая теплота (Q), необходимая для повышения температуры n молей газа с T ₁ до T ₂ , зависит не только от ΔT, но и от того, как изменяются давление и объем газа.

 

Существуют две важные теплоемкости:

Нагрев или охлаждение при постоянном объеме: Q _v = nC _v ΔT, где C _v — молярная теплоемкость при постоянном объеме.

Нагрев или охлаждение при постоянном давлении: Q _p = nC _p ΔT, где C _p – молярная теплоемкость при постоянном давлении.

 

Теплоемкость при постоянном объеме (C

_v ) для газов

Значение C _v : Подвод тепла к газу при постоянном объеме идет исключительно на увеличение внутренней энергии (E _int ) газа, не совершая никакой механической работы.

$$Q_{V} = n C_{V} \Delta T = \Delta E_{int}$$

$\Delta E_{int}$ состоит из изменения поступательной КЭ, вращательной КЭ, колебательных энергий частицы газа. Значение $E_{int}$ будет обсуждаться позже.

Для одноатомных идеальных газов:

Изменение внутренней энергии определяется изменением поступательной кинетической энергии атомов:

$$\Delta E_{int} = \Delta E_{trans} = \ frac{3}{2} n R \Delta T$$ 9{-1}$ для одноатомного идеального газа

Следовательно, теплоемкость при постоянном объеме на одну частицу:

$$C_{v} = \frac{3}{2} k_{B} $$

Для двухатомных идеальные газы:

Изменение внутренней энергии при комнатной температуре определяется как изменение поступательной кинетической энергии молекул плюс изменение вращательной кинетической энергии:

$$\begin{aligned} \Delta E_{int} & = \Delta E_{trans} + \Delta E_{rot} \\ &= \frac{3}{2} nR \Delta T + \frac{2}{2} nR \Delta T \end{aligned}$$ 9{-1}$ для двухатомного идеального газа при высокой температуре.

Многоатомные газы: с увеличением числа атомов мы можем ожидать увеличения C _v .