Пластическая деформация — это… Что такое Пластическая деформация?
Диаграмма, показывающая зависимость между силой приложенного усилия и деформацией пластичного металла.
Деформа́ция (от лат. deformatio — искажение) — изменение относительного положения частиц тела, связанное с их перемещением. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое напряжение.
Деформации разделяют на упругие и пластические. Упругие деформации исчезают[1], а пластические остаются после окончания действия приложенных сил. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия; в основе пластических — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия.
Способность веществ пластически деформироваться называется пластичностью.
Виды деформации
Наиболее простые виды деформации тела в целом:
В большинстве случаев наблюдаемая деформация представляет собой несколько деформаций одновременно. В конечном счёте, однако, любую деформацию можно свести к 2 наиболее простым:
Изучение деформации
Деформация тела вполне определяется, если известен вектор перемещения каждой его точки. Деформация твёрдых тел в связи со структурными особенностями последних изучается физикой твёрдого тела, а движения и напряжения в деформируемых твёрдых телах — теорией упругости и пластичности. У жидкостей и газов, частицы которых легкоподвижны, исследование деформации заменяется изучением мгновенного распределения скоростей.
Причины возникновения деформации твёрдых тел
Деформация твёрдого тела может явиться следствием фазовых превращений, связанных с изменением объёма, теплового расширения, намагничивания (магнитострикционный эффект), появления электрического заряда (пьезоэлектрический эффект) или же результатом действия внешних сил.
Упругая и пластическая деформация
Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки, и пластической, если после снятия нагрузки она не исчезает (во всяком случае полностью). Все реальные твёрдые тела при деформации в большей или меньшей мере обладают пластическими свойствами. При некоторых условиях пластическими свойствами тел можно пренебречь, как это и делается в теории упругости. Твёрдое тело с достаточной точностью можно считать упругим, то есть не обнаруживающим заметных пластических деформаций, пока нагрузка не превысит некоторого предела.
Природа пластической деформации может быть различной в зависимости от температуры, продолжительности действия нагрузки или скорости
 Частными случаями ползучести являются релаксация и последействие упругое. Одной из теорий, объясняющих механизм пластической деформации, является теория дислокаций в кристаллах.
Частными случаями ползучести являются релаксация и последействие упругое. Одной из теорий, объясняющих механизм пластической деформации, является теория дислокаций в кристаллах.Сплошность
В теории упругости и пластичности тела рассматриваются как «сплошные». Сплошность, то есть способность заполнять весь объём, занимаемый материалом тела без всяких пустот является одним из основных свойств, приписываемых реальным телам. Понятие сплошности относится также к элементарным объёмам, на которые можно мысленно разбить тело. Изменение расстояния между центрами каждых двух смежных бесконечно малых объёмов у тела, не испытывающего разрывов, должно быть малым по сравнению с исходной величиной этого расстояния.
Простейшая элементарная деформация
Простейшей элементарной деформацией является относительное удлинение некоторого элемента:
где
- l1 — длина элемента после деформации;
- l — первоначальная длина этого элемента.

На практике чаще встречаются малые деформации, так что e << 1.
Измерение деформации
Измерение деформации производится либо в процессе испытания материалов с целью определения их механических свойств, либо при исследовании сооружения в натуре или на моделях для суждения о величинах напряжений. Упругие деформации весьма малы, и измерение их требует высокой точности. Наиболее распространённый метод исследования деформации — с помощью тензометров. Кроме того, широко применяются тензодатчики сопротивления, поляризационно-оптический метод исследования напряжения, рентгеновский структурный анализ. Для суждения о местных пластических
Примечания
- ↑ Теоретически упругие деформации исчезают, но практически они частично остаются и накапливаются.
Литература
- Работнов Ю.
 Н., Сопротивление материалов, М., 1950;
Н., Сопротивление материалов, М., 1950; - Кузнецов В. Д., Физика твердого тела, т. 2-4, 2 изд., Томск, 1941-47;
- Седов Л. И., Введение в механику сплошной среды, М., 1962.
Wikimedia Foundation. 2010.
РАЗНИЦА МЕЖДУ УПРУГОЙ И ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИЕЙ | СРАВНИТЕ РАЗНИЦУ МЕЖДУ ПОХОЖИМИ ТЕРМИНАМИ — НАУКА
Упругая и пластическая деформация Деформация — это эффект изменения формы физического объекта при приложении к поверхности внешней силы. Силы могут быть приложены к поверхности по нормали, касательно
Упругая и пластическая деформация
Деформация — это эффект изменения формы физического объекта при приложении к поверхности внешней силы. Силы могут быть приложены к поверхности по нормали, касательной или по крутящему моменту. Если тело не меняет своей формы даже незначительно из-за внешних сил, объект определяется как идеальный твердый объект. Совершенных твердых тел в природе нет; каждый объект имеет свои деформации.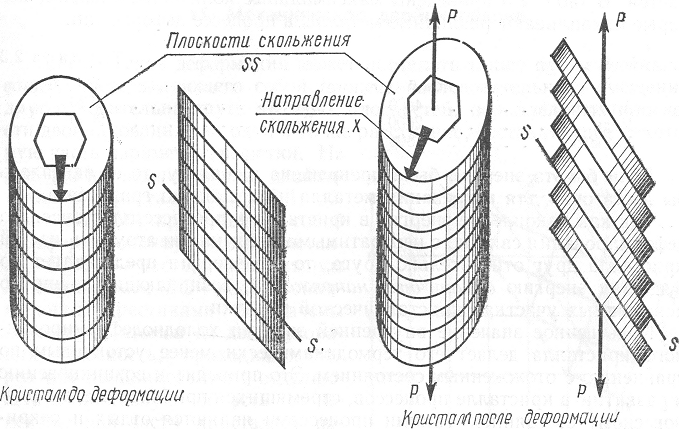 В этой статье мы собираемся обсудить, что такое упругая деформация и пластическая деформация, как они встречаются в природе и каковы их приложения.
В этой статье мы собираемся обсудить, что такое упругая деформация и пластическая деформация, как они встречаются в природе и каковы их приложения.
Упругая деформация
Когда к твердому телу прикладывается внешнее напряжение, оно имеет тенденцию разъединяться. Это приводит к увеличению расстояния между атомами в решетке. Каждый атом пытается притянуть к себе соседа как можно ближе. Это вызывает силу, пытающуюся сопротивляться деформации. Эта сила известна как деформация. Если построить график зависимости напряжения от деформации, то график будет линейным для некоторых более низких значений деформации. Эта линейная область представляет собой зону, в которой объект упруго деформируется. Упругая деформация всегда обратима. Он рассчитывается по закону Гука. Закон Гука гласит, что для диапазона упругости материала приложенное напряжение равно произведению модуля Юнга и деформации материала. Упругая деформация твердого тела — обратимый процесс, когда приложенное напряжение снимается, твердое тело возвращается в исходное состояние.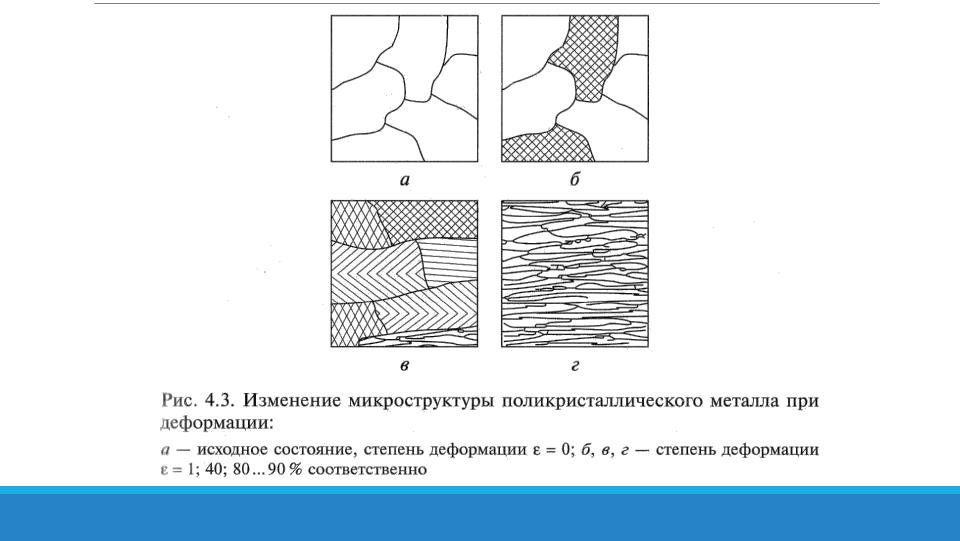
Пластическая деформация
Когда график зависимости напряжения от деформации является линейным, говорят, что система находится в упругом состоянии. Однако при высоком напряжении график проходит небольшой скачок по осям. Это предел, при котором происходит пластическая деформация. Этот предел известен как предел текучести материала. Пластическая деформация происходит в основном за счет скольжения двух слоев твердого тела. Этот процесс скольжения необратим. Пластическая деформация иногда называется необратимой деформацией, но некоторые виды пластической деформации на самом деле обратимы. После скачка предела текучести график зависимости напряжения от деформации становится плавной кривой с пиком. Пик этой кривой известен как предел прочности. После предела прочности материал начинает «сужаться», создавая неравномерность плотности по длине. Это приводит к образованию участков с очень низкой плотностью материала, что делает его легко ломким. Пластическая деформация используется при закалке металла для тщательной упаковки атомов.
В чем разница между упругой деформацией и пластической деформацией? — Основное различие между упругой деформацией и пластической деформацией состоит в том, что упругая деформация всегда обратима, а пластическая деформация необратима, за исключением некоторых очень редких случаев. — При упругой деформации связи между молекулами или атомами остаются нетронутыми, а изменяются только их длины; Явления пластической деформации, такие как скольжение пластины, происходят из-за полного расщепления связей. — Упругая деформация имеет линейную зависимость от напряжения, в то время как пластическая деформация имеет криволинейную зависимость с пиком. |
стройка, ремонт, недвижимость, ландшафтный дизайн
Основные виды деформации тела внешними силами
Основные виды деформации тела внешними силами, являются (рис. XVI.1):
а) сжатие — силы действуют по продольной оси тела и стремятся его укоротить;
б) растяжение — силы действуют по той же оси, что и в предыдущем случае, но стремятся удлинить его;
г) кручение — силы дают вращающий момент относительно продольной оси стержня; они закручивают два соседних сечения стержня вокруг общей оси и превращают прямые продольные волокна в винтообразные линии;
д) изгиб — силы дают вращающие, изгибающие моменты относительно линий перпендикулярных к оси стержня, и стремятся вызвать искривление первоначально прямого стержня (чистый изгиб без сдвига).
В почвах возникают, главным образом, сжимающие и сдвигающие напряжения.
Сжатие тела вызывается сжимающими усилиями и проявляется в укорочении длины, которое сопровождается увеличением поперечного сечения исследуемого тела.
Растяжение, напротив, вызывает удлинение по продольной оси и вместе с тем укорочение поперечных размеров испытуемого образца.
Изменение длины, выраженное в частях первоначальной длины тела, или отнесенное к ней, как к единице, называется относительным удлинением: ε = Δl/l.
Удлинение Δl до некоторого предела пропорционально нагрузке и, следовательно, в этой области деформации применим закон Гука, который выражается следующим уравнением:
где коэффициент Е называется модулем Юнга; Р — приложенная сила; S -площадь поперечного сечения образца.
Точно так же относительное поперечное сжатие определяют как отношение AS к первоначальному значению поперечного сечения:
Эта величина в известных пределах может считаться материальной константой, т.
 е. зависит только от свойств вещества данного тела и не зависит от геометрических и механических факторов. Она называется коэффициентом Пуассона.
е. зависит только от свойств вещества данного тела и не зависит от геометрических и механических факторов. Она называется коэффициентом Пуассона.Деформация металла. Физическая природа деформации металлов.
Деформация — изменение формы и размеров тела под действием напряжений. Напряжение – сила, действующая на единицу площади сечения детали.
Напряжения и вызываемые ими деформации могут возникать при действии на тело внешних сил растяжения, сжатия и т.д., а также в результате фазовых (структурных) превращений, усадки и других физико-химических процессов, протекающих в металлах, и связанных с изменением объема.
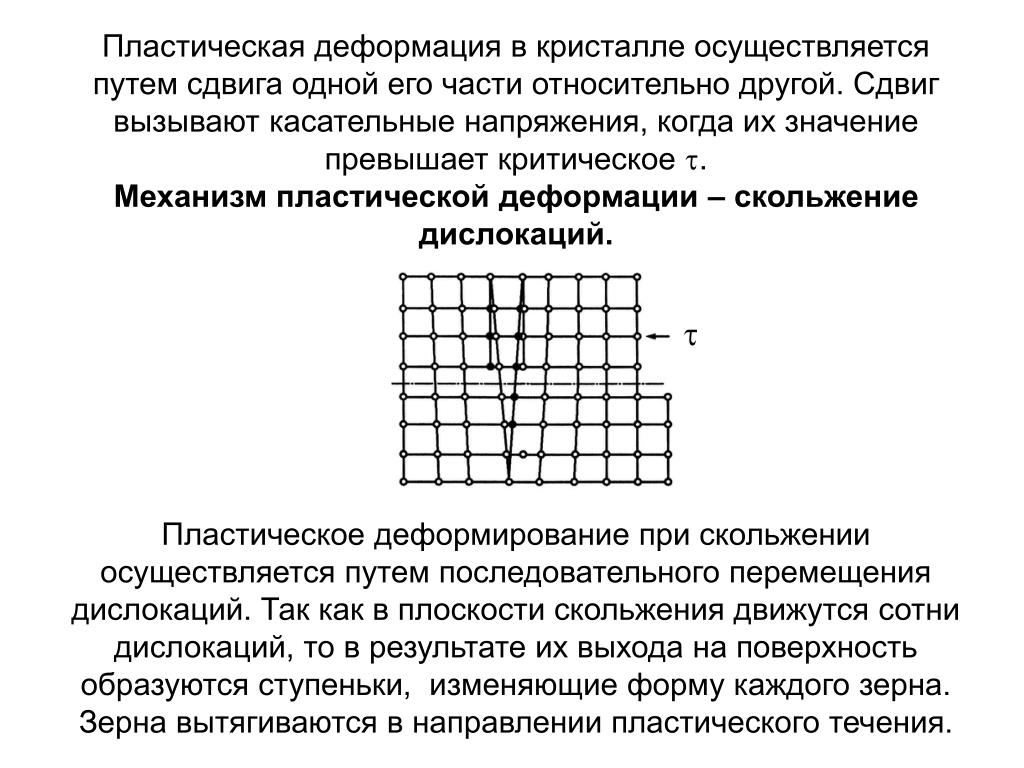
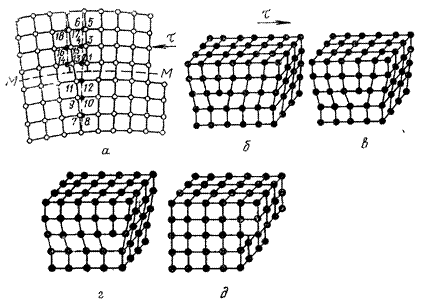
Пластическая деформация металла. Природа пластической деформации. Механизм пластической деформации. Двойникование.
Металл, находящийся в напряженном состоянии, при любом виде нагружения всегда испытывает напряжения нормальные и касательные.
Рисунок 1 — Схема возникновения нормальных и касательных напряжений в металле при его нагружении
Рост нормальных и касательных напряжений приводит к разным последствиям. Рост нормальных напряжений приводит к хрупкому разрушению. Пластическую деформацию вызывают касательные напряжения.
Рост нормальных напряжений приводит к хрупкому разрушению. Пластическую деформацию вызывают касательные напряжения.
Деформация металла под действием напряжений может быть упругой и пластической.
Упругой называется деформация, полностью исчезающая после снятия вызывающих ее напряжений. При упругом деформировании изменяются расстояния между атомами металла в кристаллической решетке. Снятие нагрузки устраняет причину, вызвавшую изменение межатомного расстояния, атомы становятся на прежние места, и деформация исчезает. Упругая деформация на диаграмме деформации характеризуется линией ОА (рисунок 2).
Рисунок 2 — Диаграмма зависимости деформации металла от действующих напряжений
Если нормальные напряжения достигают значения сил межатомных связей, то наблюдается хрупкое разрушение путем отрыва.
Рисунок 3 — Схема упругой деформации и хрупкого разрушения под действием упругих напряжений
а – ненапряженная решетка металла; б – упругая деформация; в, г – хрупкое разрушение в результате отрыва
Зависимость между упругой деформацией ε и напряжением σ выражается законом Гука:
σ = Е * ε, где
Е — модуль упругости.
Модуль упругости является важнейшей характеристикой упругих свойств металла. По физической природе величина модуля упругости рассматривается как мера прочности связей между атомами в твердом теле.
Эта механическая характеристика структурно нечувствительна, т. е. термическая обработка или другие способы изменения структуры не изменяют модуля упругости, а повышение температуры, изменяющее межатомные расстояния, снижает модуль упругости.
Пластической или остаточной называется деформация после прекращения действия вызвавших ее напряжений.
При пластическом деформировании одна часть кристалла перемещается по отношению к другой под действием касательных напряжений. При снятии нагрузок сдвиг остается, т.е. происходит пластическая деформация (рисунок 4 ). В результате развития пластической деформации может произойти вязкое разрушение путем сдвига.
Рисунок 4 — Схема пластической деформации и вязкого разрушения под действием касательных напряжений
а – ненапряженная решетка; б – упругая деформация; в – упругая и пластическая деформация; г – пластическая деформация; д, е – пластичное (вязкое) разрушение в результате среза
Деформация твёрдых тел.
 Виды деформации
Виды деформациина прошлом уроке мы с вами познакомились со строением кристаллов с их основными свойствами а сегодня будем изучать то как форма кристаллов меняется под действием внешней силой речь пойдет о деформации твердых тел тема урока деформации твердых тел . классификация видов деформации классификация видов деформацией домашнее задание на завтра конспект стримя восклицательными знаками то есть я вам расскажу больше чем учебники ну а по учебнику landsberg параграфы с 278 по 283 двести семьдесят восемь тире 283 это короткие параграфы ну и задачи лагерь в году решить следующие задачи задачи попроще 5556 и 59 и задача поинтересней 520 и 523 записали а теперь слушайте что вы не слышали деформации в самом слове уже содержится расшифровка этого понятия что-то связанное с формой представьте себе что вы гончар делаете глиняную посуду на гончарном круге вы сделали из глины допустим как горшок и поставили его перед обжигом он должен высохнуть и оказывается что после того как горшок высыхает он скукоживается его объем уменьшается это деформация представьте себе другую ситуацию биметаллическая пластина помните о восьмом классе мы с вами изучали что это такое это два металла 2 металлических пластин и с клепаные вместе заклепками одна из например цинка 2 из стали уценка коэффициент линейного расширения больше чем у стали заметным поэтому если такую пластину нагреть то длина цинковой половинки увеличится больше чем длина стальной половинки и поскольку они между собой соединены то что произойдет с пластиной она изогнется это деформация по действия нагрева мы с вами будем изучать деформацию под действием вне не силу я прикладываю внешнюю силу вызываем деформацию так что же такое деформация это любое изменение формы и объема тела запишем определение деформацией называется любое изменение деформацией называется любое изменение формы и объема тела деформации называется любое изменение формы и объема тела любое изменение формы и объема тела мы с вами будем изучать деформацию под действием внешней силы будем ли назвать где формирующая сила давайте исходить из того что мы узнали на прошлых уроках мы с вами знаем что кристаллическое тело будет речи и сейчас у кристаллических телах хотя все что сказано в принципе можно использовать и для мозга кристаллическом теле атомы находятся в положениях равновесия если мы попытаемся увеличить расстояние между атомами то есть если мы попытаемся растянуть тело-то между этими атомами начинают проявлять себя силы притяжения все тело можно представить себе как множество цепочек атомов и когда мы тело растягиваем между этими цепочками между атомами в каждой цепочки возникают силы притяжения каждая цепочка страница сократится но такие цепочки соединены параллельно и все тело состоит из множества таких цепочек и вот эти силы взаимодействия атомов сины взаимного притяжения складываясь дают нам некую силу которая приложена к моим рукам в данном случае когда я пытаюсь растянуть пружину приложена к моим рукам и называется она как сила упругости то сила упругости это равнодействующей тех сил межмолекулярного взаимодействия которые появляются при деформации еще раз обратим внимание сила упругости вследствие деформации с деформация причина сила упругости следствие может быть так вы можете возразить но пола греть как же так вы же вот деформацию вызывайте какой-то внешней силой правильно но внешние силы может не быть сил упругости при этом будет вот смотрите если я линейку сейчас вот так вот изогнут и после этого ее отпущу деформирующие силы останется нет если я ее отпустил на линейка начнет двигаться с ускорением под действием чему под действием сил упругости значит деформация осталась она не успела уйти когда я убрал руку и под действием в результате этой деформации сила упругости возникла который возвращает линейку к положению равновесия и так помню еще раз подчеркиваю деформация причина сил упругости следствие второе раз уж мы заговорили о молекулярном строении вещества каждый атом вещества находится в своем положении равновесия из-за теплового движения ум колеблется там вокруг положение равновесия но в целом неподвижен он находится в том месте где его потенциальная энергия минимально мы называем это потенциальная яма у каждого атома есть своя персональная потенциальная яма которая образована с соседними атомами если мы растягиваем например тело-то атомы покидают свое положение равновесие расстояние между ними увеличивается и они чуть-чуть выходят от серединки своей потенциальной ямы но остаются в ней когда мы перестаём действовать на тело отпускаем его атомы возвращаются в свои положи на весь и каждый по самую потенциальную яму где он до этого находился что при этом произойдет с формой тела если каждый атом вернулся в свое положение равновесия она полностью восстановится такая деформация называется абсолютно упругой давайте запишем определение деформация при которой тело полностью восстанавливает свою форму деформация при которой тело полностью восстанавливает свою форму после прекращения действия деформирующий силы полностью восстанавливает свою форму после прекращения действия деформирующие силой называется абсолютно упругой или просто у папы называется абсолютно упругой и просто итак деформации бывает упругая вот например упругой деформации линейки я ее немножечко разогнал согнул она разгибается полностью восстанавливается в форму а теперь рассмотрим другой случай допустим деформация настолько сильная что атомы покинули свои потенциальные ямы по крайней мере некоторые информация настолько что там из одного положения равновесия перескочил в какое-то другое положение равновесия если он нашел для новое положение равновесия то он там и останется там минимум его потенциальной энергии значит если мы прекратим действовать силой растягивающие и сжимающие сгибающие тело то она уже свою форму не восстановит потому что там их в прежнее потенциальной ямы не вернуться такая деформация называется пластической запишем определение деформация при которой тело полностью сохраняет новую форму деформация при которой тело полностью сохраняет свою новую форму после прекращения действия деформирующий силой полностью сохраняет свою форму после прекращения действия формирующей силой называется пластической деформация при которой тело полностью восстанавливается минуты полностью сохраняет свою новую форму после прекращения действия деформирующий силы называется пластической так вот это на самом деле два крайних случая реальность она всегда между этими двумя состояниями это модели как не бывает абсолютно черного цвета они не абсолютно белого не бывает точно так же не бывает абсолютно упругой и абсолютно пластической деформации если формация малая то ее можно считать абсолютно упругой мы не замечаем чтобы тело не возвращалась в свое прежнее состояние чтобы она что она не восстанавливает свои формы до конца хотя он и ребята школьники многие могут так согнуть эту линейку что она уже потом полностью свою форму не восстановлен или если мы возьмем кусочек пластилина если его согнуть он свою новую форму сохраняем это пластическая деформация отсюда и название пластилин но на самом деле если деформировать даже это пластилин едва-едва то можно заметить что он частично свою форму восстанавливает очень ярко какая частичная упругая частично пластическая деформация проявляется вот на такой линейки линейка не ломай специально для школьников сделано чтобы они могли себя проявить я ее сгинаю она на первых порах сохраняется в деформацию но постепенно выравнивается она нет вот сейчас я ее отпущу она не будет в такой форме она чуть-чуть разогнулась но не полностью вот эта реальность между абсолютно упругой и пластической деформации это самое интересное зато вот эти два вида деформации самые простые то есть они более всего поддаются изучению поэтому мы с вами сегодняшний урок посвятим исключительно упругой деформации то что вам рассказал это уже один из видов классификации деформации информации можно делить на упреки пластически и какие-то промежуточные а теперь второй вид классификации по характеру изменения формы тела классификация по характеру изменения формы тела классификация деформации по характеру изменения формы тела тут мы поставим 1 римская а здесь мы поставим 2 классификация на упругие пластические это один вид классификации а по характеру изменения формы тела второй вид 1 простейший вид деформации растяжения черточка с сжатия растяжение-сжатие давайте нарисуем как выглядит деформации растяжения и сжатия на самом деле растяжение-сжатие то одно и то же с точностью до знака поэтому мы будем рисовать деформацию растяжения уезжать или в к себе представить пусть у нас имеются стержень один конец которого закреплен на этот стержень с другого конца мы будем действовать какой-то силой эту силу я буду обозначать пунктиром под действием этой силы стержень растянется вот эта сила f между атомами начнут проявлять себя силы притяжения и поэтому стержень своим концом будет то тело которое сообщила ему эту силу тянуть в противоположную сторону по третьему закона мету это и будет та самая сила которую мы называем силой упругости она по модулю buy точно такое же если стержень и подвижен вот так будет пытаться вернуть стержень в прежнее положение возвратить его форму напоминаем мы говорим об упругих деформациях поскольку нам предстоит с этой деформации иметь дело довольно подробно давайте сразу попробуем количественное и описать пусть первоначальная длина стержня корее а длина деформированного стержня случае деформации растяжения будет больше она будет равна н плюс дельта я не она стала больше на величину in time величина дельта р вот она имеет свое название она называется абсолютное обвинение бель-иль абсолютная удлинение каких единицах измеряется она все в метрах как любая длина а теперь давайте введем еще одну величину которая более содержательно почему более содержательно сейчас станет ясно разделим абсолютно и удлинение на первоначальную длину мы получим величину которая является безразмерной она обозначается греческой буквой эпсилон и носит название относительного удлинения относительное удлинение это безразмерная величина давайте запишем определение что это такое относительным удлинением называется физическая величина равная относительное удлинение называется физическая величина равная отношение абсолютного удлинения физическая величина равная отношению абсолютного удлинения к первоначальной длине тела отношению абсолютного удлинения к первоначальной длины тела нетрудно догадаться что если эпсилон положительное то это будет деформация какое растяжении или сжатии и растяжении если version отрицательная то это будет деформация сжатие чем интересна эта величина оказывается что она характеризует не деформацию тело целом а деформацию материала из которого это тело сделано вот смотрите допустим мы возьмем на эту резинку подвесим киеву она вызовет деформацию резинки соответственно деформированная резинка силой упругости подействовать на эту беру силой направленной вверх вот это удлинение резинки зависит от того какой длинны и сама резинка если резинка длинное длине не будет побольше если резинка короткая удлиняя не будет поменьше но если мы возьмем резину в два раза короче то абсолютное удлинение в этой ситуации будет в два раза меньше чем несли резина у нас имеет полную длину а если мы абсолютно и удлинение разделим на первоначальную глину то мы получим всегда одно и то же независимо от того короткая резинка длинная или совсем короткая относительное удлинение характеризует деформацию материала независимо от того какой длины тела сделано в этом случае из этого материала а раз так то это более информативной а величина не зависит от длины давайте еще одну величину все которое в дальнейшем нам понадобится стержень действует на окружающие тела силой упругости введём поперечное сечение стержня площадь с и рассмотрим вот такую величину отношение силы упругости и лошади поперечного сечения о которой она распределена эта величина обозначается буквой сигма только она никакого отношения к коэффициенту поверхностного натяжения и удельной поверхностной энергии не имеет алфавит гораздо беднее чем природа поэтому физики понятий больше чем букв в алфавите эта величина называется механическое напряжение механическое напряжение механическое напряжение запишем определение механическим напряжением называется физическая величина равная механическим напряжением называется физическая величина равное отношение силы упругости физическая величина равна отношению силы упругости площади поперечного сечения по которому эта сила распределена отношение силы упругости к площади поперечного сечения по которому она распределена каких единицах измеряется механическое напряжение давайте посмотрим единицы измерения сигма сила измеряется в ньютонах площадь в квадратных метрах а что это такое ньютон делить на квадратный метр как называется эта единица а вообще как называется отношение силы действующий перпендикулярно некоторой поверхности к площади поверхности это называется давление каких единицах измеряется давление в паскалях относительно механическое напряжение тоже измеряется в паскалях эта величина очень близкое по смыслу к давлению если вы сжимаете стержень то давление которое вы на него производите как раз равно механическому напряже в объеме сдержит вот эти две величины обе описывают не деформацию тела и не силу приложенную к телу деформацию материала из которого это тело сделано и механическую нагрузку на сам материал эти величины наверное как-то связаны друг с другом эту связь мы установим на следующем уроке а сейчас нам нужно продолжить классификацию видов деформации и давайте заодно продемонстрируем нам этой модели особенность деформации растяжения ржания вот тело его она состоит из а там эти атомы можно считать расположен вот такими слоями назовем их атомными плоскостями когда мы тело подвергаем деформации сжатия или растяжения то эти плоскости остаются параллельными друг другу но они у давайте так смотреть но они смещаются друг относительно друга в какую сторону в направлении перпендикулярная самим плоскостям оставаясь параллельными друг другу они смещаются в направлении перпендикулярном плоскости возьмем это на заметку а теперь перейдем к следующему его деформации уже так подробно его описано не будем но память деформация сдвига второй сдвиг рассмотрим тело форме прямоугольного параллелепипеда которые мы прикрепим к какой-то поверхности приклеим например вот такое чем приклеили в поверхности стола по действуем на него силой направленной вдоль этой поверхности в результате тело изменит свою форму вот так он самади формирующая сила я ее по-прежнему буду обозначать пунктиром это не формирующейся результате такой деформации возникнет сила упругости которая будет пытаться мешать это и силе дальнейшем деформировать тело силу упругости приложена к тому телу которое вызвало а теперь посмотрите как можно описать количественно это этот вид деформации его можно описать с помощью угла вот этот угол гамма угол сдвига при деформации сдвига атомной плоскости тоже смещаются на давайте посмотрим на эту модель как они смещаются если при деформации сжатия а не смещались направлении перпендикулярном самим плоскостям что при деформации сдвига они смещаются в том же направлении в котором лежат эти плоскости параллельно самим плоскость а ну а теперь смотрите что дальше можно сделать если мы возьмем какую-то сложную деформацию рассмотрим например вот такую то ее можно разложить на 2 простые деформации вот эта точка одновременно движется вниз перпендикулярного танатос костями и вправо вдоль оси y и вдоль оси x смещение на любой вектор можно представить как смещение в доле y en tu le six значит сложную деформацию можно представить как комбинацию вот такой растяжение-сжатие и такой деформации сдвига любую сложную формацию можно представить как комбинацию растяжение сжатия и сдвига поэтому эти два вида деформации являются основными и закономерности этих деформаций прежде всего надо изучать третий вид деформации деформация изгиба представим себе тело напишем название изгиб представим себе тело лежащие на двух опорах мы можем к нему силу направленную вниз под действием этой силы тела деформируются вот эта сила например можно подвесить или поставить гику просто на это тело это деформация из него анти мы говорили только что о том что любую деформацию можно представить себе как комбинацию сдвига и растяжение-сжатие давайте посмотрим что будет здесь давайте рассмотрим небольшой участок вот этого тела вот как он выглядит этот небольшой участок посмотрите вот модель этого тела что будет с расстояние между атомными плоскостями если я это тело согнул внизу расстояние между атомами плоскости на увеличится верха уменьшится значит нижняя часть растянута а верхние зажата то есть деформация изгиба это комбинация сжатие и растяжение самое интересное то что здесь есть некая поверхность которая не испытывает ни растяжение и сжатие вот это нейтральная поверхность митральная поверхность если эта поверхность не испытывает ни растяжение и сжатие расстояние между атомами не меняются то тогда она оказывается не деформированы и значит там не возникает никаких механических напряжений когда мы можем ее просто так же мы можем ее просто удалить из тела и это никак не скажется на прочности и упругих свойствах этого тела почти никак не скажется но зато при этом уменьшится масса расход материала при сохранении практически стопроцентно прочности поэтому при конструировании различных устройств поступают как правило следующим образом но давайте посмотрим на это тело с этой стороны нейтральная поверхность вот она лук вид отсюда вот нейтральную поверхность мы можем удалить этот материал и при этом по отношению к вот такой деформации изгиба тело практически сохранить свои упругие свойства удалить этот материал можно различными способами например вот так можно вот так можно вот так это называется труба какой такой профиль называется двутавр похоже на две буквы то я вот верхняя половинка и нижняя половинка а это швеллер скажите где нибудь вы видели такие формы такие bow строительные балки если пойти на стройку посмотреть из чего делают дома их делают из двутавров и швеллеров из труб они легче но при той же самой прочность представьте себе велосипед у которого храма не трубчатая он был бы жутко тяжелый а самолет если бы его делали не из трубчатых набирали не из трубчатых конструкций из сплошных он бы просто не смог подняться воздух кстати а где вы встречали еще деформацию сдвига смотрите допустим у вас есть две пластины соединенные заклепками скреб она и вот так и одна пластина подвергается действием силы в эту сторону а другую пластину тянут в эту сторону сами заклепки при этом вот здесь испытывают деформацию сдвига если потянуть очень сильно здесь может быть сдвиг настолько сильный что атомы скользнуть от ровной плоскости материала одни начнут проскальзывать относительно других это уже будет называться разрушению вот такое нет разрушений является срезом говорят заклепки срезала а где мы используем в быту такую деформацию причем на уровне когда происходит разрушение когда мы пользуемся ножницами дамы что-то режем ножницами то как раз мы вызываем деформацию сдвига настолько сильную что материал не выдерживает и разрушаемся применяется деформация сборе деформации растяжения и сжатия где встречаются тросы веревки канадкой испытывают информацию растяжения колонны строительных поддерживающие на портик дома деформация сжатие следующий вид деформации это деформация кручения выяснили что изгиб это комбинация растяжения и сжатия а вот теперь смотрим последний вид деформации кручения допустим у нас есть тело имеющую форму цилиндра и мы его приклеим приварим прикрепим к какой-то основе чтобы было видно как деформируются тело покрасим его полосками направленными вдоль оси цилиндра и теперь давайте приложим к делу не силу а пару сил если мы приложим просто силу в горизонтальном направлении это вызовет деформацию сдвига а что такое поросил вспоминаем 9 класс это две силы направлены в противоположную сторону не лежащие на одной прямой и равные поможет приложим пару сил одну силу пусть она действует сюда а вторую силу пусть она действует сюда такая же по модулю сила мечты эти две силы вызову деформацию кручения при этом заметить ее можно глядя на вот эти линии они перестанут быть вертикальными они вот так наклоняться вот эта деформация кручения мы с вами говорили о том что любую деформацию можно свести к растяжению и сжатию или сдвигу а что из себя представляет собой деформации отключения давайте ее сейчас здесь воспроизведем вот деформация кручения скажите пожалуйста в плоскости смещаются в направлению параллельным плоскостям или перпендикулярным параллельно значит кручение это разновидность сдвига рада величина сдвига разная на разных расстояниях от оси вращения с краю сдвиг больше угол сдвига с краю больше а ближе к центру вот здесь меньше радиус да здесь угол сдвига меньше поэтому такой сдвиг называется неоднородным сдвигов любой вид деформации можно разложить на растяжение сжатия и сдвиг есть целый раздел механики которое называется теория упругости у физиков это называется теории упругости он позволяет рассчитать деформацию тел если известна как например хроническое напряжение если известна как деформирована тело в любых случаях технических вузов этот раздел называется сопротивление материалов это очень сложная наука и и очень не любят студенты например политехнического института сейчас называется университет они называют сопромат за промыть потому что сдать этот предмет очень сложно он довольно-таки сложно поэтому мы на следующем уроке коснемся только с самых простых видов деформации но о чем пойдет речь узнаете через пять минут перерыв
растяжение, сжатие, кручение, сдвиг, изгиб
О чем эта статья
Не вдаваясь в теоретические основы физики процессом деформации твердого тела можно назвать изменение его формы под действием внешней нагрузки. Любой твердый материал имеет кристаллическую структуру с определенным расположением атомов и частиц, в ходе приложения нагрузки происходит смещение отдельных элементов или целых слоев относительно, другими словами возникают дефекты материалов.
Любой твердый материал имеет кристаллическую структуру с определенным расположением атомов и частиц, в ходе приложения нагрузки происходит смещение отдельных элементов или целых слоев относительно, другими словами возникают дефекты материалов.
Виды деформации твердых тел
Деформация растяжения
Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.
Схема растяжения образца
Посмотрите прибор измеряющий деформацию растяжения →
Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов.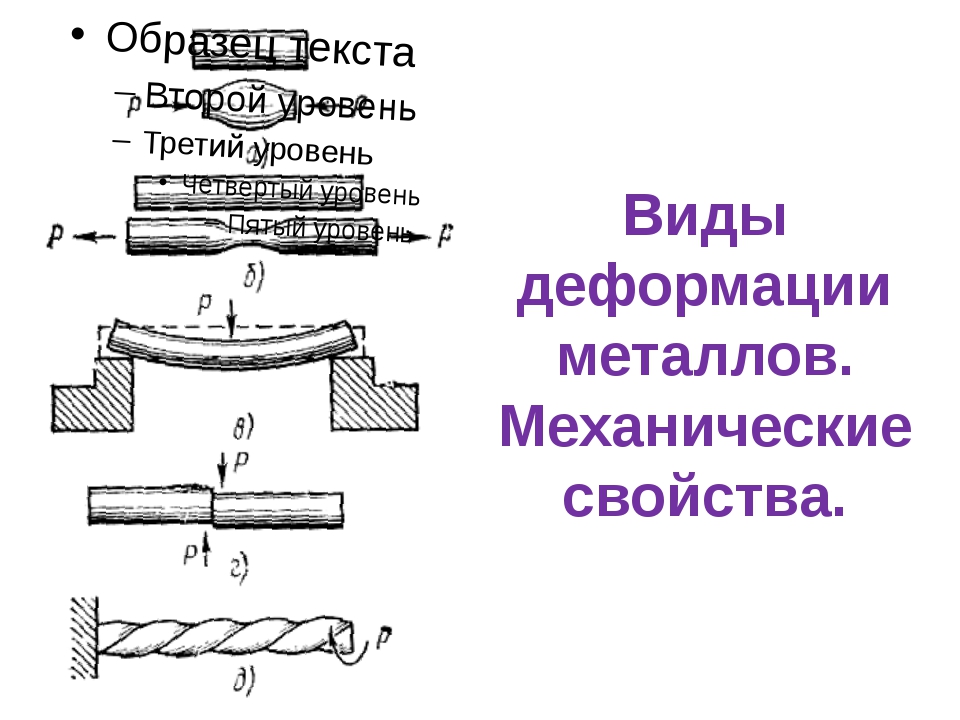 В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:
В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:
- воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация)
- воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация)
- разрушаться на пределе прочности
Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами.
Деформация сжатия
Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».
Схема сжатия образца
В качестве примера можно привести тот же прибор что и в деформации растяжения немного выше.
Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры. Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности.
Деформация сдвига
Деформация сдвига — вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой. На предельные нагрузки сдвига испытываются все крепежные элементы — болты, шурупы, гвозди. Простейший пример деформации сдвига – расшатанный стул, где за основание можно принять пол, а за плоскость приложения нагрузки – сидение.
Схема сдвига образца
Посмотрите прибор измеряющий деформацию сдвига →
Деформация изгиба
Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.
Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.
Схема изгиба образца
Посмотрите прибор измеряющий деформацию изгиба →
Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и другие.
Деформация кручения
Деформация кручения – вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. На кручение работают валы машин, шнеки буровых установок и пружины.
Схема кручения образца
Посмотрите прибор измеряющий деформацию кручения →
Пластическая и упругая деформация
В процессе деформации важное значение имеет величина межатомных связей, приложение нагрузки достаточной для их разыва приводит к необратимым последствиям (необратимая или пластическая деформация). Если нагрузка не превысила допустимых значений, то тело может вернуться в исходное состояние (упругая деформация). Простейший пример поведения предметов, подверженных пластической и упругой деформацией, можно проследить на падении с высоты резинового мяча и куска пластилина. Резиновый мяч обладает упругостью, поэтому при падении он сожмется, а после превращения энергии движения в тепловую и потенциальную, снова примет первоначальную форму. Пластилин обладает большой пластичностью, поэтому при ударе о поверхность оно необратимо утратит свою первоначальную форму.
За счет наличия деформационных способностей все известные материалы обладают набором полезных свойств – пластичностью, хрупкостью, упругостью, прочностью и другими. Исследование этих свойств достаточно важная задача, позволяющая выбрать или изготовить необходимый материал. Кроме того, само по себе наличие деформации и его детектирование часто бывает необходимо для задач приборостроения, для этого применяются специальные датчики называемые экстензометрами или по другому тензометрами.
Опубликована 12-04-12.
Если вам понравилась статья нажмите на одну из кнопок ниже
Разница между упругой и пластической деформацией (Наука и природа)
Эластичная и пластическая деформация
Деформация — это эффект изменения формы физического объекта при воздействии внешней силы на поверхность. Силы могут быть приложены как нормальные, тангенциальные или крутящие моменты на поверхности. Если тело не меняет свою форму, даже слегка из-за внешних сил, объект определяется как идеальный твердый объект. Совершенных твердых тел в природе нет; каждый объект имеет свои собственные деформации. В этой статье мы собираемся обсудить, что такое упругая деформация и пластическая деформация, как они встречаются в природе, и каковы их применения.
Упругая деформация
Когда к твердому телу прикладывается внешнее напряжение, оно стремится разойтись. Это приводит к увеличению расстояния между атомами в решетке. Каждый атом пытается притянуть своего соседа как можно ближе. Это вызывает силу, пытающуюся противостоять деформации. Эта сила известна как напряжение. Если построить график зависимости напряжения от деформации, график будет линейным для некоторых более низких значений деформации. Эта линейная область является зоной, в которой объект упруго деформируется. Упругая деформация всегда обратима. Он рассчитывается по закону Гука. Закон Гука гласит, что для диапазона упругости материала приложенное напряжение равно произведению модуля Юнга и деформации материала. Упругая деформация твердого тела является обратимым процессом, когда снятое приложенное напряжение снимается, твердое тело возвращается в исходное состояние..
Пластическая деформация
Когда график зависимости напряжения от деформации является линейным, говорят, что система находится в упругом состоянии. Однако, когда напряжение высокое, участок проходит небольшой скачок по осям. Это предел, при котором он становится пластической деформации. Этот предел известен как предел текучести материала. Пластическая деформация происходит в основном из-за скольжения двух слоев твердого тела. Этот процесс скольжения необратим. Пластическая деформация иногда называется необратимой деформацией, но некоторые виды пластической деформации на самом деле являются обратимыми. После скачка предела текучести график зависимости напряжения от деформации становится плавной кривой с пиком. Пик этой кривой известен как предел прочности. После достижения максимальной прочности материал начинает «сужаться», создавая неравномерность плотности по длине. Это делает области материала очень низкой плотности, что делает его легко разрушаемым. Пластическая деформация используется при закалке металла для тщательной упаковки атомов.
В чем разница между упругой деформацией и пластической деформацией? — Основное различие между упругой деформацией и пластической деформацией заключается в том, что упругая деформация всегда обратима, а пластическая деформация необратима, за исключением некоторых очень редких случаев.. — При упругой деформации связи между молекулами или атомами остаются нетронутыми, но только изменяют свою длину; Явления пластической деформации, такие как скольжение пластины, происходят из-за полного деления связей. — Упругая деформация имеет линейную зависимость от напряжения, а пластическая деформация — изогнутую зависимость, имеющую пик. |
Пластическая деформация — обзор
5.8 Влияние одноосной пластической деформации на БН
В нескольких работах [24, 26, 32, 33, 35–37] по БН показано, что напряжение, приложенное в упругом режиме материала оказывает на сигнал BN эффекты, которые отличаются от эффектов, создаваемых напряжением в пластическом режиме, выходящем за предел упругости. Пластическая деформация в ферромагнитных материалах вызывает несколько изменений магнитных свойств этих материалов в зависимости от уровня деформации, что особенно затрудняет изучение этого сложного явления.
Пластическая деформация углеродистых сталей, как правило, приводит к снижению активности BN [26, 37]. Хотя при очень малых пластических деформациях наблюдалось небольшое увеличение активности BN. Исследование пластической деформации проводилось несколькими авторами, в том числе Стефанита и соавторами [35]. Они изучили эволюцию параметров BN от упругого режима к пластическому, а также микроструктурные изменения, которые происходят в некоторых типах сталей. В дополнение к этому Baldev et al.В [33] проанализировано влияние пластической деформации на временную зависимость BN (огибающая сигнала BN). Эти работы показали, что приложенное напряжение (в пределах упругости) изменяет магнитное поведение материала из-за магнитоупругого эффекта [29,35]. Пластическая деформация изменяет магнитное поведение из-за микроструктурных эффектов пластической деформации следующим образом:
- (i)
Увеличение количества мест закрепления в виде дислокаций и клубков дислокаций, которые представляют собой препятствия для движение доменных стенок.
- (ii)
Создание кристаллографической текстуры, изменяющей направление оси легкого намагничивания.
- (iii)
Появление локальных остаточных напряжений, расположенных на границах зерен и вокруг дислокаций.
Из рис. 5.23 видно, что для этих значений деформации Vrms уменьшается с увеличением пластической деформации. Этот процесс объясняется, в основном, увеличением количества дислокаций и образованием клубков дислокаций [35,36], которые представляют собой значительные препятствия для смещения стенок, препятствующие их движению.В предыдущих работах было обнаружено, что для самых высоких уровней деформации материал не насыщается магнитно, даже при высокой интенсивности приложенных магнитных полей, которые показывают, что стенки доменов прочно закреплены, предотвращая насыщение материала.
Рис. 5.23. Зависимость BN (Vrms) от пластической деформации сталей 1005–1070 при больших деформациях.
С другой стороны, было обнаружено, что при меньших пластических деформациях могут возникать более сложные явления, однако в настоящий момент нет подходящего объяснения рассматриваемой проблемы, и ее исследование продолжается [32].
На рис. 5.24 показана зависимость MPV и Vrms BN от пластической деформации для значений пластической деформации до 5%.
Рис. 5.24. Зависимость BN от пластической деформации стали AISI / SAE 1045 и ASTM A36 для малых деформаций MPV (A) и Vrms (B).
Рис. 5.24 показывает, что сигнал BN в целом уменьшается для этих значений деформации. Однако при деформациях от 0,4% до 1% может произойти усиление сигнала BN. Этот феномен еще не получил точного объяснения.Большинство теорий объясняют этот процесс случайным присутствием остаточного напряжения на границах зерен, которое способствует, а не препятствует движению 90-градусных доменов, которые очень чувствительны к напряжению. Другое возможное объяснение состоит в том, что с образованием дислокаций структура доменов улучшается, образуя множество стенок под углом 90 градусов, которые очень чувствительны к растяжению. Следовательно, при наличии в материале остаточных напряжений эти домены обладают высокой подвижностью, а из-за их большого количества происходит увеличение сигнала BN.Этот процесс исчезает при более высоком приложенном напряжении, потому что большое количество образующихся дислокаций препятствует перемещению 90 градусов доменных стенок.
Еще одно свидетельство сложности процесса пластической деформации и его корреляции с магнитными свойствами получено из анализа спектра мощности сигнала BN для различных значений пластической деформации: 0% –4% (рис. 5.25A и B).
Рис. 5.25. Зависимость спектра мощности сигнала BN для различных значений пластической деформации в сталях AISI / SAE 1045 (A) и ASTM A36 (B).В области между пунктирными линиями наблюдается четкая зависимость от деформации.
Из рисунка видно, что для низких и высоких частот нет явной зависимости спектра мощности от пластической деформации. Однако для средних значений частоты между ними существует очевидная корреляция. Объяснение этого явления неясно, хотя его можно отнести к следующей причине: когда стальной образец подвергается одноосной пластической деформации, напряжение, имеющееся на поверхности образца, отличается от напряжения во внутреннем объеме образца.Это приводит к несбалансированному остаточному напряжению в поверхностных слоях. Известно, что существует корреляция между частотой сигнала BN и глубиной, с которой они излучаются. Чем выше частота излучаемого сигнала, тем ближе к поверхности возникают выбросы BN. Скачки высоких частот зависят от поверхностных факторов, таких как шероховатость поверхности; по этой причине они не имеют явной зависимости от деформации. Промежуточная область представляет собой нижнюю непосредственную поверхность, где имеется четкая корреляция сигнала BN с деформацией: сигнал BN уменьшается с пластической деформацией.Для еще более низких частот получается информация обо всем материале, поскольку низкие частоты исходят как от поверхности, так и от нижнего объема. Таким образом, эта часть спектра мощности содержит информацию из нескольких областей, корреляция которых с деформацией различна, что может быть причиной того, что корреляция между BN и пластической деформацией на низких частотах не очевидна.
На рис. 5.26 показана зависимость оболочки BN от пластической деформации для сталей AISI / SAE 1045 и ASTM A36.
Рис. 5.26. Зависимость оболочки BN от пластической деформации для AISI / SAE 1045 (A) и ASTM A36 (B).
На этом рисунке показано, что оболочка пластической деформации подвергается следующим воздействиям на оболочку BN:
- (a)
Амплитуда оболочки уменьшается с пластической деформацией.
- (б)
Ширина оболочки увеличивается с пластической деформацией.
- (c)
Огибающая имеет тенденцию делиться на два пика, амплитуда которых уменьшается.
Объяснение этого явления объясняется увеличением количества дислокаций и остаточных напряжений: увеличение дислокаций предотвращает движение как 180-градусных стенок, так и 90-градусных стенок, которые сильно закреплены. Чтобы сдвинуть эти стены, требуется высокая напряженность поля; вот почему иногда может появиться третий пик при очень высоких значениях напряженности поля, как это видно в случае 1% -ной деформации.
Разница между упругой деформацией и пластической деформацией
В любом инженерном деле твердые конструкции подвергаются внешней нагрузке.Такую нагрузку можно в общих чертах разделить на две категории: нормальная нагрузка и нагрузка сдвига. Растягивающая и сжимающая нагрузки — это два разных типа нормальной нагрузки. Все другие типы нагружения, такие как изгиб, скручивание и т. Д., В основном представляют собой комбинацию этих трех основных типов нагружения. Когда к твердому телу приложена достаточная внешняя нагрузка, оно деформируется. Самым основным механизмом деформации является смещение слоев атомов из их исходного положения в решетке под действием внешней силы.
Когда такое смещение или смещение происходит на очень малой длине, атомы могут вернуться в свои соответствующие узлы решетки после снятия внешней нагрузки. Такая деформация называется упругой деформацией. Таким образом, упругая деформация носит временный характер и не причиняет вреда конструкциям. Однако, если атомы смещаются на большую длину, деформация становится постоянной и полное восстановление становится невозможным. Такая деформация называется пластической деформацией, и из-за нее вся конструкция может изменить свою первоначальную форму и размер.Различные сходства и различия между упругой деформацией и пластической деформацией представлены ниже в виде таблицы.
- Любой тип нагрузки (нормальный, сдвигающий или смешанный) может привести к обоим типам деформаций.
- Пластическая деформация возможна только после упругой деформации материала. Таким образом, без упругой деформации пластическая деформация невозможна.
- Полезны как упругие, так и пластические деформации; однако на основе приложения.
| Упругая деформация | Пластическая деформация |
|---|---|
| Упругая деформация — это временная деформация под действием внешней нагрузки. | Пластическая деформация — это остаточная деформация. |
| После снятия внешней нагрузки с упруго деформированного тела оно восстанавливает свою первоначальную форму. | При пластической деформации тело сохраняет деформированную форму даже после снятия внешней нагрузки. |
| При упругой деформации атомы материала временно смещаются из своего исходного узла решетки. Они возвращаются в исходное положение после снятия внешней нагрузки. | При пластической деформации атомы твердого тела постоянно смещаются из своего исходного узла решетки. Они не возвращаются в исходное положение даже после снятия внешней нагрузки. |
| Упругая деформация характеризуется свойством Elasticity. По определению, эластичность — это свойство твердого материала, благодаря которому он стремится восстановить свою форму после снятия внешней нагрузки. | Пластическая деформация характеризуется свойством Пластичность.По определению, пластичность — это свойство твердого материала, благодаря которому он сохраняет свою деформированную форму даже после снятия внешней нагрузки. |
| Степень упругой деформации очень мала. | Величина пластической деформации довольно велика. |
| Внешняя сила, необходимая для упругой деформации твердого тела, довольно мала. | Сила, необходимая для пластической деформации, также выше. |
| Энергия, поглощаемая материалом во время упругой деформации, называется модулем упругости. | Полная энергия, поглощенная материалом в области упругой и пластической деформации, называется модулем ударной вязкости. |
| Закон упругости Гука применим в этой упругой области. | Закон Гука неприменим, если материал пластически деформирован. |
| Большинство твердых материалов демонстрируют линейное поведение напряжения-деформации в этой упругой области. | Кривая напряжения-деформации нелинейна в пластической области. |
| Материал сначала подвергается упругой деформации под действием внешней нагрузки. | Пластическая деформация возникает после ее упругой деформации под действием внешней нагрузки. |
| Механические и металлургические свойства твердого материала остаются неизменными при его упругой деформации. | Многие свойства твердого материала значительно изменяются при пластической деформации. |
Список литературы
- Книга: Материаловедение и инженерия Каллистера Р.Баласубраманиам (Wiley India). Купить эту книгу Книга
- : Введение в проектирование машин В. Б. Бхандари (McGraw Hill Education India Private Limited). Купить эту книгу
- Книга: Учебник сопротивления материалов Р. К. Бансала (Laxmi Publications Private Limited). Купить эту книгу
- Книга: Прочность материалов С. С. Раттана (Tata McGraw Hill Education Private Limited). Купить эту книгу
Типы локализации пластической деформации и этапы диаграмм нагружения металлических материалов с различной кристаллической структурой
Л. Б. Зуев, В. И. Данилов, «Самовозбуждающаяся волновая модель пластической деформации твердых тел», Фил. Mag. , 79 , № 1, 43–57 (1999).
Google ученый
Зуев Л. Б., Данилов В. И. Природа крупномасштабных корреляций в пластическом потоке // ФММ. Твед. Tela , 39 , № 8, 1399–1403 (1997).
Google ученый
Л. Б. Зуев, “Волновые явления при низкоскоростном пластическом течении твердых тел”, Ann. Phys. , 11 / 12 , 965–984 (2001).
Google ученый
Баранникова С.А., Данилов В.И., Зуев Л.Б. Локализация двойниковой пластической деформации в монокристаллах отожженного γ-Fe // Журн. Тех. Физ. , 72 , № 9, 63–66 (2002).
Google ученый
Зуев Л. Б., Семухин Б. С., Зариковская Н. В. Реконструкция автоволновой структуры при деформации поликристаллического алюминия // ЖТФ. Phys. , 46 , № 5, 563–568 (2001).
Артикул Google ученый
E. Macherauch, «Plastische Deformation von Polykristallen», Z. Metallkunde , 55 , № 2, 60–82 (1964).
Google ученый
Иванова В. С., Ермишкин В. А., Прочность и пластичность тугоплавких металлов и монокристаллов, , Металлургия, Москва (1976).
Google ученый
Трефилов В.И., Горная И.Д., Моисеев В.Ф. и др. Линейная стадия деформационного упрочнения поликристаллических объемноцентрированных кубических металлов и сплавов // Докл. Акад. Наук Укр. ССР, сер. А , № 11, 81–85 (1982).
Google ученый
Конева Н. А., Козлов Е. В. Физическая природа стадий пластической деформации // Структурные уровни пластической деформации и разрушения , Наука, Новосибирск (1990).
Google ученый
R. Honeycomb, Пластическая деформация металлов , Cambridge University Press, Кембридж (1968).
Google ученый
B. Jauol, «Etude de la forme des courbes deformation Plastigue», J. Mech. Phys. Твердые тела , № 2, 95–114 (1957).
Google ученый
В. И. Трефилов, В. Ф. Моисеев, Е. П. Печковский, Деформационное упрочнение и разрушение поликристаллических металлов, , Наукова думка, Киев (1989).
Google ученый
Т. М. Полетика, Г.Нариманова Н., Колосов С.В., Зуев Л.Б. Локализация пластического течения в промышленных циркониевых сплавах // ПМТФ. Мех. Tech. Phys. , 44 , № 2, 262–270 (2003).
Артикул Google ученый
Л. Б. Зуев, В. И. Данилов, Б. С. Семухин, Пространственно-временное упорядочение при пластической деформации твердых тел. Физ. Металл. , 3 , № 3, 237–304 (2002).
Google ученый
Данилов В. И., Шляхова Г. В., Зуев Л. Б. и др. Стадии пластического течения и макролокализация деформации в поликристаллах Fe-3% Si // ФММ. Металл. Металловед. , 98 , № 3, 107–112 (2004).
Google ученый
Л.Б. Зуев, В.И. Данилов, С.А. Баранникова, И.Ю. Зыков, “Локализация пластических течений как новый вид волновых процессов в твердых телах”, Матем. Sci. Англ. А , 319–321, 160–163 (2001).
Данилов В. И., Баранникова С. А., Зуев Л. Б. Автоволны локализованной деформации на начальных стадиях пластического течения монокристаллов // ЖТФ. Phys. , 48 , № 11, 1429–1435 (2003).
Артикул Google ученый
Какой пример пластической деформации? — Цвета-NewYork.com
Какой пример пластической деформации?
Примером материала с большим диапазоном пластической деформации является влажная жевательная резинка, которую можно растянуть в десятки раз по сравнению с исходной длиной.Под действием растягивающего напряжения пластическая деформация характеризуется областью деформационного упрочнения, областью образования шейки и, наконец, разрушением (также называемым разрывом).
Почему это называется пластической деформацией?
Этот тип деформации включает растяжение связей, но атомы не проскальзывают друг мимо друга. Когда напряжение достаточно для постоянной деформации металла, это называется пластической деформацией.
Что такое пластическая деформация в физике?
Пластическая деформация — это необратимая деформация, которая возникает, когда материал подвергается растягивающим, сжимающим, изгибающим или скручивающим напряжениям, которые превышают его предел текучести и вызывают его удлинение, сжатие, коробление, изгиб или скручивание.
Как определить остаточную пластическую деформацию?
После того, как материал достиг предела упругости или деформировался, дальнейшее растяжение приведет к необратимой деформации. После сдачи не вся нагрузка будет восстановлена при снятии нагрузки. Пластическая деформация определяется как остаточная безвозвратная деформация.
Как предотвратить пластическую деформацию?
Метод улучшения
- понизить температуру формы.
- Увеличенное время охлаждения.
- понизить температуру материала.
Пластическая деформация — это хорошо или плохо?
Основным эффектом любого метода тяжелой пластической деформации (SPD) является повышение механической прочности за счет уменьшения размера зерна, и среди этих методов только равноканальное угловое прессование (ECAP) позволяет производить заготовки промышленных размеров.
Повышает ли пластическая деформация пластичность?
Например, с увеличением пластической деформации предел текучести Cu и Al монотонно увеличивается, а их удлинение до разрушения (пластичность) уменьшается.Мы сообщаем о необычайном сочетании высокой прочности и высокой пластичности, которое достигается в металлах, подверженных сильной пластической деформации (SPD).
Где происходит пластическая деформация?
Пластическая деформация в виде скольжения происходит по плотноупакованным плоскостям решетки, где потребность в энергии для движения дислокаций минимальна. Скольжение внутри кристалла продолжается до тех пор, пока линия дислокации не достигает конца кристалла, где возникает видимая ступенька — так называемая полоса скольжения.
Почему пластическая деформация — это плохо?
Пластическая деформация очень чувствительна к дискретным дефектам, как микроскопическим, так и атомным, в материале. Поскольку положения атомов меняются во время пластической деформации, напряжение, необходимое для поддержания потока материала, весьма чувствительно к кристаллической структуре.
Какие три типа деформации?
Когда горная порода подвергается возрастающему напряжению, она проходит 3 последовательных стадии деформации. Упругая деформация — деформация обратима.Пластичная деформация — деформация необратима. Разрушение — необратимая деформация, при которой материал разрушается.
Почему пластическая деформация постоянна?
После снятия внешней нагрузки с упруго деформированного тела оно восстанавливает свою первоначальную форму. При пластической деформации тело сохраняет деформированную форму даже после снятия внешней нагрузки. При пластической деформации атомы твердого тела постоянно смещаются из своего исходного узла решетки.
Обратима ли пластическая деформация?
В физике и материаловедении пластичность, также известная как пластическая деформация, — это способность твердого материала подвергаться остаточной деформации, необратимому изменению формы в ответ на приложенные силы.
Кто сделал первый пластик?
Лео Бэкеланд
Что такое процесс деформации?
Процессы деформации преобразуют твердые материалы из одной формы в другую. Начальная форма обычно проста (например, заготовка или листовая заготовка) и пластически деформируется между инструментами или штампами, чтобы получить желаемую окончательную геометрию и допуски с требуемыми свойствами (Altan, 1983).
Что означает деформация?
1: изменение формы или формы также: продукт такого изменения.2: действие деформации: состояние деформации. 3: изменение к худшему.
Ковка — это процесс деформации?
Ковка — это процесс деформации, при котором рабочая деталь сжимается между двумя штампами с использованием удара или постепенного давления для формирования детали. Технологии изготовления металла классифицируются в соответствии со схемой, показанной на рисунке.
Что такое эффективность деформации?
Следовательно, эффективность процесса деформации выражается как: (4.35) Эффективность процессов деформации, выраженная в процентах, колеблется от 30–60% для экструзии от 75–95% для прокатки. Пластическая деформация часто может привести к повышению температуры детали.
Что такое процесс первичного формования?
Первичные производственные процессы Эти процессы используются для преобразования сырья или лома в основной продукт первичной формы и размера. Различные основные производственные процессы: Литье. Формование, такое как ковка, прокатка, экструзия и т. Д.Соединение, такое как сварка, пайка и т. Д.
Что такое процесс обработки металлов давлением?
Обработка металлов давлением — это процесс изготовления, при котором конструкционные детали и компоненты создаются из металлических листов или труб. Основной процесс формования металла будет сгибать или деформировать металлическую заготовку до желаемой геометрической формы. Все полагаются на компоненты, полученные в процессе обработки металлов давлением.
Какие 3 основных дефекта обнаруживаются в процессах формовки листового металла?
Морщины, трещины и упругая отдача — три наиболее распространенных дефекта, встречающихся при штамповке листового металла.
Какие бывают виды формовки?
Некоторые примеры процессов формования:
- Ковка.
- Экструзия.
- Прокатка.
- Обработка листового металла.
- Ротационная обжимка.
- Накатка резьбы.
- Формование взрывом.
- Электромагнитное формование.
Какие два основных типа процесса обработки металла?
Обычно процессы обработки металлов давлением можно разделить на две большие группы.Один из них — объемное формование, а другой — формование листового металла. Объемная деформация относится к использованию для формования сырья, которое имеет низкое отношение площади поверхности к объему.
Что такое процесс формования?
Формование — это механический процесс, используемый в обрабатывающей промышленности, где материалы (в основном металлы) подвергаются пластической деформации и приобретают требуемые формы и размеры за счет приложения подходящих напряжений, таких как сжатие, сдвиг и растяжение.
Сколько существует видов земледелия?
8 основных типов систем земледелия в Индии — Civilsdaily.
Какие 5 типов земледелия?
1. Натуральное хозяйство: —
- Интенсивное натуральное хозяйство: —
- Первобытное натуральное хозяйство: —
- Сменная обработка: —
- Торговое зерновое хозяйство: —
- Коммерческое смешанное сельское хозяйство: —
- Коммерческое земледелие: —
Какое сельское хозяйство наиболее прибыльно?
Вот самые прибыльные бизнес-идеи в области сельского хозяйства:
- Сельскохозяйственная ферма.
- 10 самых прибыльных бизнес-идей животноводства.
- Производство органических удобрений «Биогумус».
- Бизнес сухих цветов.
- Бизнес по распространению удобрений.
- Органическая ферма «Зеленый дом».
- Птицеводство.
- Грибное хозяйство.
Какие 4 основных типа земледелия?
Типы сельского хозяйства включают натуральное хозяйство, смешанное сельское хозяйство, кочевое скотоводство, коммерческие плантации, животноводство и т. Д.Сельское хозяйство включает разведение животных и выращивание сельскохозяйственных культур для получения сырья и продуктов питания.
Какие 7 отраслей сельского хозяйства?
Как написано ниже, в этих сферах сельского хозяйства имеется большое количество отраслей.
- Агрономия.
- Садоводство.
- Селекция растений / Генетика.
- Почвоведение.
- Агрометеорология.
- Сельскохозяйственная биотехнология.
- Агротехника.
- Расширение сельского хозяйства.
Что происходит при пластической деформации? — MVOrganizing
Что происходит при пластической деформации?
Пластическая деформация — это необратимая деформация, которая возникает, когда материал подвергается растягивающим, сжимающим, изгибающим или скручивающим напряжениям, которые превышают его предел текучести и вызывают его удлинение, сжатие, коробление, изгиб или скручивание.
Объем изменяется при пластической деформации?
В большинстве кристаллических материалов, в том числе в большинстве металлов, пластическая деформация принимает форму скольжения атомных плоскостей друг относительно друга, опосредованного дислокациями.Нет никакого изменения объема, связанного с пластической деформацией.
Что происходит, когда материал деформируется?
Когда к металлу или другому конструкционному материалу прилагается достаточная нагрузка, это приводит к изменению формы материала. Это изменение формы называется деформацией. Другими словами, упругая деформация — это изменение формы материала при низком напряжении, которое можно восстановить после снятия напряжения.
Где происходит пластическая деформация?
Пластическая деформация возникает, когда материал подвергается напряжению выше предела упругости, т.е.е. за пределом текучести, как показано на рисунке 1. Результирующая пластическая деформация является постоянной и не может быть восстановлена простым снятием напряжения, вызвавшего деформацию.
Какие 3 типа деформации?
Когда горная порода подвергается возрастающему напряжению, она проходит 3 последовательных стадии деформации. Упругая деформация — деформация обратима. Пластичная деформация — деформация необратима. Разрушение — необратимая деформация, при которой материал разрушается.
Как рассчитывается пластическая деформация?
Пластическая деформация получается путем вычитания упругой деформации, определяемой как значение истинного напряжения, деленное на модуль Юнга, из значения общей деформации (см. Рисунок 1). Рис. 1. Разложение общей деформации на упругую и пластическую составляющие.
Какие два типа деформации бывают?
Деформация бывает двух видов:
- Постоянная деформация — также известная как пластическая деформация, она необратима.Это тип деформации, который сохраняется даже после снятия приложенных сил.
- Временная деформация — также известная как упругая деформация, она обратима.
Что такое пластическая деформация?
Этот тип деформации вызван перегруппировкой атомов в материале и не является обратимым. Когда напряжение снимается, в материале сохраняется пластическая деформация.
Какой пример пластической деформации?
Пластическая деформация описывает постоянное изменение формы или размера в результате напряжения; Напротив, упругая деформация — это только временное изменение размера.С другой стороны, примеры пластической деформации включают изгиб стального стержня при растяжении или разрушение стекла при сжатии.
Какие примеры пластмасс?
Примеры пластмасс
- Полиэтилентерефталат: ПЭТ или ПЭТФ.
- Полиэтилен высокой плотности: HDPE.
- Поливинилхлорид: ПВХ.
- Полипропилен: PP.
- Полистирол: ПС.
- Полиэтилен низкой плотности: LDPE.
Какой пример поведения пластика?
Например, твердый кусок металла, который сгибается или толкается в новую форму, демонстрирует пластичность, поскольку в самом материале происходят постоянные изменения.В технике переход от упругого к пластическому поведению известен как податливость.
Что такое процесс деформации?
Процессы деформации преобразуют твердые материалы из одной формы в другую. Начальная форма обычно проста (например, заготовка или листовая заготовка) и пластически деформируется между инструментами или штампами, чтобы получить желаемую окончательную геометрию и допуски с требуемыми свойствами (Altan, 1983).
Фрезерование — это процесс деформации?
Обработка, фрезерование и растачивание — это процессы вычитания, которые создают или изменяют формы.Основное внимание в этой главе уделяется второй категории, процессам твердой деформации, в которых плотный твердый исходный материал преобразуется в форму за счет приложения механических сил.
Каковы причины важности процессов объемной деформации?
Причины, по которым процессы объемной деформации важны, включают: (1) они способны к значительному изменению формы при использовании горячей обработки, (2) они положительно влияют на прочность детали, когда используется холодная обработка, и (3) большая часть процессы производят мало материальных отходов; некоторые из них являются процессами чистой формы.
Повышает ли горячая обработка прочность?
Горячая обработка улучшает технические характеристики детали, поскольку она заменяет микроструктуру на микроструктуру с мелкими зернами сферической формы. Эти зерна увеличивают прочность, пластичность и ударную вязкость материала.
Повышает ли горячая прокатка твердость?
До сих пор был сделан вывод, что при горячей прокатке увеличение высоты канавок валка, которое было функцией его расширения, вызванного параметрами процесса, привело к увеличению толщины проката, что повлияло на механические свойства прокатываемых образцов. такие как предел прочности на разрыв, предел текучести.
Что такое процесс горячей и холодной обработки?
Холодная штамповка или холодная обработка — это любой процесс металлообработки, при котором металлу придают форму ниже его температуры рекристаллизации, обычно при температуре окружающей среды. Такие процессы контрастируют с методами горячей обработки, такими как горячая прокатка, ковка, сварка и т. Д.
Каковы преимущества и недостатки горячей обработки перед холодной обработкой?
Преимущества и недостатки Горячая обработка Снижение предела текучести, поэтому с ним легче работать и требуется меньше энергии или усилий.Повышение пластичности. Повышенные температуры увеличивают диффузию, которая может удалить или уменьшить химические неоднородности. При деформации поры могут уменьшиться в размерах или полностью закрываться.
Когда материал подвергается холодной обработке?
Аннотация: Холодная обработка — это пластическая деформация металлов ниже температуры рекристаллизации. В большинстве случаев такое холодное формование производится при комнатной температуре. Основные операции холодной обработки можно разделить на выжимку, гибку, резку и волочение.
Работает ли отжиг в горячем состоянии?
Когда металл подвергается горячей обработке, ему придают форму, когда его температура превышает температуру рекристаллизации. В этих условиях отжиг происходит во время обработки металла, а не как отдельный процесс. Горячая обработка металла обычно проводится при температуре около 0,6 от его точки плавления.
Повышает ли холодная деформация пластичность?
Из-за металлургических изменений, происходящих с металлом во время холодной обработки, пластичность металла снижается по мере увеличения объема холодной обработки.Эти изменения приводят к снижению текучести и прочности металла на разрыв, а также к увеличению его пластичности, что позволяет проводить дальнейшую холодную обработку.
Почему пластичность увеличивается с температурой?
При температурах выше пика образование диффузных пустот снижает пластичность. Следовательно, увеличение скорости деформации увеличивает величину деформации кручения по сравнению с увеличением скорости роста полости, и повышается пластичность.
Как повысить пластичность конструкции?
Боковое армирование улучшает пластичность, предотвращая преждевременные разрушения при сдвиге и ограничивая зону сжатия, тем самым увеличивая деформационную способность железобетонной балки.Пластичность можно увеличить за счет • Уменьшения% растянутой стали (pt).
Повышает ли закалка прочность?
Сталь с закалочной закалкой В зависимости от содержания углерода и легирующих элементов в стали может остаться более твердая и хрупкая микроструктура, такая как мартенсит или бейнит, когда она подвергается закалочному упрочнению. Эти микроструктуры приводят к увеличению прочности и твердости стали.
Почему производится закалка?
В металлургии закалка чаще всего используется для упрочнения стали путем индуцирования мартенситного превращения, когда сталь должна быстро охлаждаться через ее эвтектоидную точку, температуру, при которой аустенит становится нестабильным.Это позволяет начинать закалку при более низкой температуре, что значительно упрощает процесс.
В чем разница между отжигом и закалкой?
В процессе отжига структура не изменяется, в основном для устранения внутренних напряжений металла. Сталь нагревается до критической температуры выше 30-50 ℃. Сравните закалку с отжигом и нормализацией, главное отличие — быстрое охлаждение, цель — получить мартенсит.
Сколько существует видов закалки?
Три типа
Что такое физическое тушение?
Механизм, связанный с передачей энергии, обозначается как физическое тушение: молекула тушителя дезактивирует 1O2 в триплетное нереактивное основное состояние, набирает энергию в триплетное возбужденное состояние, а затем легко теряет свою энергию в окружающую среду и возвращается в исходное состояние.
Что такое нормализация?
Нормализация — это процесс термообработки, который используется для повышения пластичности и прочности металла после того, как он подвергся процессам термического или механического упрочнения. Этот нагрев и медленное охлаждение изменяют микроструктуру металла, что, в свою очередь, снижает его твердость и увеличивает пластичность.
Почему закалка в масле лучше, чем в воде?
Масло предпочтительнее традиционной охлаждающей среды, состоящей из воды, поскольку оно снижает риск деформации или растрескивания за счет более равномерного и более быстрого охлаждения металлов.
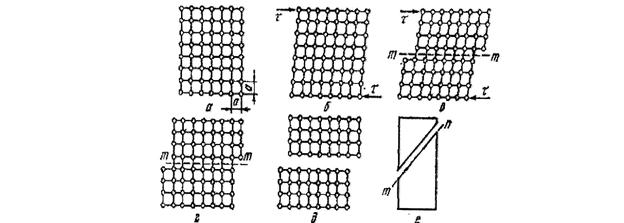
Деформация металлов и ее виды
Изменение размеров форм материи под действием приложенных сил называется «деформацией». Это вызвано либо механическим действием внешних сил, либо различными физическими и физико-химическими процессами. Для образования различных металлических форм необходима деформация металлов. Деформированные или механически обработанные металлы намного превосходят литые металлы, из которых они изготовлены.
Типы деформации металла:Деформации металла бывают двух типов:
1.Упругая деформация, и
2. Пластическая деформация.
1. Упругая деформация:
Упругая деформация — это деформация, которая исчезает при снятии нагрузки. Он предшествует (имеет место раньше) пластической деформации. Эта деформация возникает при приложении напряжения к металлической детали.
Фиг. 3.1 [(i), (ii), (iii)] показывает форму атомов до нагрузки, после нагрузки при растяжении и сжатии соответственно. Когда прилагается растягивающая нагрузка, деталь становится немного длиннее, тогда как сжимающая нагрузка укорачивает деталь.
При снятии нагрузки (растягивающей или сжимающей) металлическая деталь или образец восстанавливает свою первоначальную форму (размер). В пределах диапазона упругости деформация является результатом небольшого удлинения элементарной ячейки в направлении растягивающей нагрузки или небольшого сжатия в направлении сжимающей нагрузки.
Для упругой деформации напряжение почти пропорционально напряжению. Соотношение между напряжением и деформацией при упругой деформации известно как модуль упругости или модуль Юнга (E).Это характеристика типа металла, и ее величина зависит от силы притяжения между атомами металла.
Напряжения сдвига также возникают в кристаллических структурах в инженерных приложениях. Они вызывают смещение одной плоскости атомов относительно соседней плоскости атомов. Упругая деформация определяется как тангенс угла сдвига. Отношение между напряжением сдвига и деформацией сдвига известно как модуль жесткости при сдвиге (C).
2. Пластическая деформация:
Это деформация, которая сохраняется даже после снятия нагрузки.Пластическая деформация наблюдается при напряжениях, превышающих предел упругости. В отличие от упругой деформации, которая в простейших случаях зависит в первую очередь от напряжения, пластическая деформация обычно зависит от напряжения, температуры и скорости деформации.
Пластическая деформация связана со смещением атомов внутри зерен и в конечном итоге вызывает необратимые изменения формы материала. Растягивающие, сжимающие и скручивающие напряжения могут вызвать пластическую деформацию.
Процесс пластической деформации обычно применяется на важных металлургических операциях формовки. Операции включают прокатку котельных плит, волочение проволоки, экструзию телефонных кабелей, штамповку автомобильных деталей и т. Д.
В металлах пластическая деформация обычно происходит за счет процесса «скольжения».
Накладка :Скольжение определяется как деформация сдвига, при которой атомы перемещаются на множество межатомных расстояний в одной кристаллической плоскости по атомам другой кристаллической плоскости.На рис. 3.2 показан процесс скольжения под действием сдвигающей нагрузки (в монокристалле). Из-за пластической деформации кристалл разделяется на слои или блоки скольжения, которые смещены относительно друг друга и разделены тонкими слоями, в которых произошло значительное смещение атомов.
Эти промежуточные слои с сильно искаженной решеткой называются «плоскостями скольжения». Скольжение легче происходит по одним направлениям и плоскостям кристалла, чем по другим. Это показано на рис.3.3, где монокристаллический металл ГПУ пластически деформировался.
Критическое разрешенное напряжение сдвига :
Напряжение сдвига, необходимое для скольжения по плоскости кристалла, называется критическим разрешенным напряжением сдвига.
Для получения выражения для касательного напряжения на плоскости скольжения рассмотрим кристалл, подверженный растягивающей нагрузке (P), действующей в направлении оси (рис. 3.4). Эта сила P создает силу сдвига в плоскости скольжения и силу, нормальную к плоскости скольжения.Если β — угол между направлением силы и нормалью к плоскости скольжения, то площадь плоскости скольжения будет α / cos β, где A — площадь поперечного сечения, перпендикулярного направлению силы P.
Составляющая силы P, действующая в плоскости скольжения в направлении скольжения = P cos α, где α — угол между направлением силы и направлением скольжения. ∴
∴ Критическое разрешенное напряжение сдвига,
Это уравнение известно как закон Шимда.Скольжение происходит с минимальной осевой силой, когда оба угла α и β равны 45 °. В этих условиях τ кр равно половине осевого напряжения P / A. Приведенное напряжение сдвига меньше по сравнению с осевым напряжением для любой другой ориентации кристалла, и по мере приближения α или β к 90 ° оно падает до нулевого значения.
Для каждого материала критическое напряжение сдвига является постоянным и зависит от типа силы сцепления. Он не зависит от относительной ориентации приложенного напряжения, направления скольжения, но зависит от температуры, чистоты, эффекта незначительной деформации, скорости деформации и поверхностных эффектов.
Проскальзывание произойдет, если под действием приложенного напряжения разрешенное напряжение сдвига достигнет критического значения τ кр . При очень низкой скорости деформации в кристалле возможно пластическое течение при напряжении сдвига ниже критического напряжения сдвига. Этот вид деформации называется ползучестью.
I. Критическое разрешенное напряжение сдвига (CRSS)
Это зависит от следующих факторов:
(i) Состав:
Значение CRSS увеличивается с увеличением содержания сплава,
(ii) Чистота:
Ценность CRSS увеличивается с увеличением содержания примесей (растворимые примеси более эффективны, чем нерастворимые).
(iii) Степень предварительной деформации:
Значение CRSS увеличивается с увеличением степени предшествующей деформации.
(iv) Температура:
Значение CRSS обычно уменьшается с повышением температуры и резко падает до нуля при температуре плавления или температуре солидуса в сплавах. На CRSS не влияет напряжение, нормальное к плоскости скольжения.
II. Квитанция:
Фактически, он состоит из относительного смещения параллельных плоскостей скольжения за счет сдвигающего действия разрешенного напряжения сдвига и одновременного поворота активной системы скольжения в направлении растяжения.
Хотя скольжение напоминает простое относительное скольжение двух параллельных плоскостей, оно отличается в следующих отношениях:
а. Скольжение ограничено определенными плоскостями и направлениями, причем плоскости определяются внутренними направленными силами.
г. Степень скольжения ограничена межатомным расстоянием или целым кратным этого расстояния. Сопротивление продолжающемуся скольжению увеличивается (но практически постоянно при скольжении).
г. Часть этой энергии скольжения сохраняется в кристалле как потенциальная (деформационная) энергия, в отличие от полного рассеивания (в виде тепла) энергии скольжения.
В микроскопическом масштабе деформация не является равномерной, а локализуется на плоскостях скольжения и в пределах полос скольжения.
Расстояние между плоскостями скольжения в полосе скольжения может быть порядка 200 Å, тогда как расстояние между соседними полосами может быть в 100 раз больше.
Проскальзывание на каждой плоскости может быть порядка нескольких микрон.
Минимальная сила, необходимая для создания скольжения, на несколько порядков меньше, чем мы ожидаем, исходя из наших знаний о кристаллических структурах и межатомных силах.В типичном металле теоретическое критическое разрешенное напряжение сдвига составляет примерно 10 11 дин / см 2 , в то время как экспериментальное измерение составляет примерно 10 7 дин / см 2 .
Умеренная деформация даже при низких температурах не меняет кардинально свойств, и нет никаких признаков разрушения решетки.
По мере увеличения величины приложенного напряжения количество активных плоскостей скольжения и расстояние скольжения по этим плоскостям увеличивается.
Иногда происходит дуплексное скольжение, особенно в металлах FCC. Скольжение сопровождается вращением плоскости скольжения в направлении приложенного растягивающего напряжения, и для продолжения деформации требуется постоянное увеличение напряжения. Это вращение активной плоскости скольжения к оси растяжения вызывает вращение других систем скольжения.
Если одна из этих систем поворачивается в положение, в котором разрешенное напряжение сдвига в системе больше, чем критическое разрешенное напряжение сдвига, но меньше того, которое требуется для продолжения скольжения в первой системе, тогда скольжение будет иметь место в новой системе.По мере увеличения нагрузки в обеих системах может происходить скольжение поочередно между ними.
Twinning :Двойникование — это процесс, при котором часть кристалла принимает ориентацию, которая делает эту часть зеркальным отображением родительского кристалла.
Деформация двойникованием наиболее распространена в ГПУ-металлах, и ее влияние на другие заключается в перемещении частей зерен таким образом, что они приобретают благоприятную ориентацию для проскальзывания. Твиннинг возникает внезапно и сопровождается звуком.Всем известный крик олова — результат двойникования.
На рис. 3.6 показана классическая атомная картина двойникования. Плоскость двойникования расположена под прямым углом к бумаге. Если приложить напряжение сдвига, кристалл повернется вокруг плоскости двойникования. Область слева от плоскости двойникования не деформирована. Справа от этой плоскости плоскости атомов сдвинулись таким образом, что решетка стала зеркальным отражением плоскости двойника.
Таким образом, механизм двойникования можно описать как простое скольжение одной плоскости атомов по следующей, причем степень движения каждой плоскости пропорциональна ее расстоянию от плоскости двойникования.На рис. 3.7 показано схематическое изображение двойникования.
В случае скольжения смещение кратно межатомному расстоянию, но при двойниковании смещение, создаваемое скольжением одной плоскости по соседнему, составляет долю единичного скольжения. Это вызывает различие в ориентации двойниковых и несвязанных областей в кристалле, и при полировке и травлении их можно легко различить под микроскопом.
Близнецы могут быть двух типов:
1.Механические близнецы:
Изготовлены путем механической деформации. Они производятся из металлов BCC или HCP в условиях высокой скорости нагружения (ударной нагрузки) и пониженной температуры.
2. Двойники отжига:
Они получают в результате отжига после пластической деформации.
В отношении твиннинга стоит отметить следующие моменты:
и. Двойникование происходит, когда атомы в слое внутри кристалла перестраиваются во время деформации таким образом, что слой создает зеркальное отображение по отношению к соседнему слою исходного кристалла,
ii.Плоскость двойникования — это плоскость симметрии, связывающая двойниковый слой с исходным кристаллом.
iii. Хотя двойникование не является действительным вращением плоскостей, удобно визуализировать двойниковую часть кристалла, как если бы она вращалась вокруг плоскости симметрии. Движение при двойниковании — это действительно сдвиг соседних плоскостей.
Все задействованные плоскости смещаются в одном направлении, и каждая плоскость смещается на величину, пропорциональную ее расстоянию от плоскости двойникования. Таким образом, двойникование можно рассматривать как деформацию скольжения, в которой участвует каждая плоскость атомов в двойниковом слое, в отличие от нормального скольжения, при котором между активными плоскостями может находиться несколько наклонных плоскостей.
iv. При двойниковании каждая плоскость атомов сдвигает небольшую, но определенную долю межплоскостного расстояния по отношению к соседним плоскостям. Этот сдвиг приводит к эффективной ориентации близнеца. Это контрастирует с отсутствием изменения ориентации при скольжении.
v. Двойник кристалла может участвовать в деформации двумя способами:
а. Само двойное образование может привести к значительному изменению формы, или
г. Это может способствовать дальнейшему скольжению, размещая плоскости потенциального скольжения в более благоприятных положениях по отношению к приложенному напряжению.Решетка обычно более эффективна в создании деформации.
vi. Критическое разрешенное напряжение сдвига (CRSS) для двойникования (как и CSSR для скольжения) зависит от состава, чистоты, предшествующей деформации и температуры.
Фрэнк Рид Источник:Именно по небольшому количеству кристаллических плоскостей происходит интенсивное скольжение, и в ходе этого процесса перемещаются несколько сотен дислокаций. Это указывает на то, что должны существовать некоторые эффективные создатели дислокаций, известные как «Источники Франк Рида».
См. Рис. 3.29. Сначала фиксируется краевая дислокация на двух дефектах. Затем линия дислокации вздувается под действием напряжения в плоскости скольжения, а на более поздней стадии граница исходной дислокации становится нестабильной и изгибается обратно вокруг этих двух точек, как показано стадиями 1–3 на диаграмме.
Наконец, на стадии 4 происходит дальнейшее самопроизвольное расширение выпуклости и образуется замкнутая петля, которая движется наружу к границе зерен. При исчезновении петли снова создается исходная краевая дислокация.Если напряжение сохраняется, образуется еще один цикл, и цикл повторяется.
Источники Франк-Рида при холодной работе срабатывают на каждой активной плоскости скольжения и общее количество дислокаций увеличивается до 10 12 на квадратный см.
Деформация поликристаллических материалов :Хотя процесс деформации в основном такой же, деформация поликристаллического материала намного сложнее.Пластическая деформация в поликристаллическом агрегате никогда не бывает однородной. Большая прочность поликристаллических материалов обусловлена границами зерен. Границы зерен обеспечивают большее сопротивление скольжению, чем внутренняя часть зерен, отчасти из-за разницы в направлении скольжения между кристаллами.
Так как некоторые кристаллы в поликристаллическом материале всегда ориентированы так, что их направление скольжения находится в плоскости максимального сдвига, они будут пытаться подойти к напряжению, сравнимому с напряжением для монокристалла.Если окружающие кристаллы достаточно эластичны, они будут допускать незначительную податливость этих слабых кристаллов. Таким образом, постепенно начинается всеобщая уступчивость.
Аморфные материалы поддаются разным механизмам.
Деформация поликристаллического металла вызывает значительные структурные изменения. В целом пластическая деформация влияет на все физико-химические и механические свойства металла.
Поликристаллический металл имеет следующие характеристики:
(i) Разрешенное напряжение сдвига зависит от ориентации зерен.
(ii) Когда такой металл / сплав загружается, различные зерна не имеют одинаковой ориентации.
(iii) Внутри кристалла существует ряд возможных плоскостей скольжения.
Стадии процесса деформирования поликристаллических заполнителей:
I. Все кристаллы под нагрузкой деформируются только упруго. Агрегат ведет себя идеально эластично.
II. Некоторые кристаллы переходят предел упругости и пластически деформируются.Если нагрузка снимается, между упруго и пластически деформированными кристаллами возникают напряжения, которые постепенно возвращают пластически деформированные кристаллы к их первоначальной форме. Это постепенное возвращение называется «эластичным последействием». Монокристаллы не проявляют этого эффекта. Если образец многократно нагружать и разгружать, он постепенно затвердевает в процессе работы (или деформации), и последующий эффект исчезает.
III. На третьем этапе большинство кристаллов пластически деформируются, материал выходит за предел упругости, и можно измерить остаточную деформацию.
IV. Наконец, пластическая деформация во всех кристаллах становится значительной, и начинается заметная текучесть агрегата.
Механизм деформации (в поликристаллических материалах):
После того, как поликристаллический (металлический) образец нагружен, первая деформация происходит за счет скольжения в зернах, которые имеют благоприятную ориентацию, а затем она перемещается к другим зернам (хотя скольжение от одного зерна к другому затруднено). Там, где плоскость скольжения встречается с границей зерен, происходит скопление дислокаций, создавая концентрацию напряжений, которая помогает перемещению дислокации в следующем зерне через границу зерен.Отсутствует нарушение когерентности зерен и образование отверстий на границах зерен, что предполагает изменение формы, требующее множественной ориентации плоскостей скольжения.
В то время как в поликристаллических кубических металлах деформация происходит скольжением; в гексагональных металлах это происходит только тогда, когда приложенное напряжение вызывает двойникование.
Явление предела текучести :Введение :
На рис. 3.30 показана диаграмма «напряжение-деформация», полученная при деформации растяжением при нагружении образца из низкоуглеродистой стали (отожженного).Явление предела текучести было первоначально обнаружено в этом материале. Первая более высокая точка, при которой начинается текучесть (U), называется верхним пределом текучести, а другое более низкое значение (U), имеющее большее напряжение, известно как нижний предел текучести. Напряжение, необходимое для начала пластического течения, выше, чем для поддержания пластического течения, как видно на диаграмме, после определения предела текучести.
Из-за дислокаций в образце наблюдается деформационное упрочнение. Это приводит к тому, что кривая напряжения-деформации приобретает плавный и постепенный рост.Это называется явлением предела текучести, которое указывает на то, что относительное удлинение, возникающее при постоянном напряжении, оказывает важное влияние на значение предела текучести.
Имеется большая энергия деформации, связанная с дислокацией кристаллической решетки, которая будет пытаться уменьшить ее во время перестройки кристаллической структуры. Примеси также уменьшают перемещение дислокаций. Таким образом, требуется более высокий стресс.
Важность :
Предел текучести имеет значение при практическом использовании различных металлов.
Помимо железа и стали, пределы текучести наблюдались у поликристаллических металлов, таких как молибден, титан и алюминиевые сплавы.
Предел текучести имеет значение, потому что как только металл поддается и пластическая деформация начинается в данной области, металл в этой точке эффективно размягчается и претерпевает относительно большую пластическую деформацию. Затем эта деформация распространяется на материал, примыкающий к области, которая деформировалась из-за концентрации напряжений на границе между деформированной и недеформированной областями.
Предел текучести очень важен для производителя, который штампует или вытягивает тонкие листы этих материалов при формовании, например, автомобильных кузовов и других объектов.
Связанные эффекты от предела текучести :
Следующие эффекты связаны с пределом текучести:
1. Деформации ленты Людерса и носилок.
2. Деформационное старение.
3. Голубая хрупкость.
4. Эффект апельсиновой корки.
1. Luder Bands:
Это маркировка на поверхности образца для испытаний на растяжение, сформированная в точках концентрации напряжений, таких как галтели. Их образование указывает на достижение верхнего предела текучести. Фактически, более низкий предел текучести, возможно, является напряжением, необходимым для распространения полос Людера.
Эти полосы обычно расположены под углом примерно от 45 ° до 50 ° к оси растяжения.
После того, как полоса людера сформировалась на одной галтели образца для испытания на растяжение, она может перемещаться по измерительной длине образца.
Когда образец проходит стадию удлинения до предела текучести, эти полосы растекаются по образцу и покрывают всю измерительную длину, тем самым показывая, что вся измерительная длина была перенапряжена.
Полосы Людера часто возникают при вытяжке и штамповке, когда рельефная маркировка поверхности называется деформациями подрамника. Чтобы избежать этих деформаций на готовых деталях, листы перед операциями прессования перенапрягаются посредством прохода отпускных валков, так что явление предела текучести устраняется.
2. Деформационное старение:
Деформационное старение подразумевает изменение свойств сплава со временем после предварительного деформирования.
Деформационное старение обычно связано с явлением предела текучести.
Если испытательный образец, который был перенапряжен для снижения предела текучести, оставлен в покое или состарился после пластической деформации, предел текучести возвращается с более высоким напряжением.
Если образец разгружают и повторно испытывают без старения, то предел текучести будет возникать из-за слабых дислокационных эффектов атмосферы углерода и упрочнения из-за увеличения значения напряжения.
Деформационное старение характерно для товарного чугуна и стали, хотя продолжается и для других металлов.
Это важный фактор усталости и ползучести.
3. Голубая хрупкость:
Этот эффект возникает при увеличении диапазона температур испытания; предел текучести становится менее выраженным.
Разрушение образца происходит при низкой деформации с высоким напряжением.
На участке диаграммы напряжение-деформация показана более крутая кривая с быстрым образованием последовательных пределов текучести из-за эффектов быстрой диффузии и дислокации.
Этот эффект проявляется примерно при 160–300 ° C.
4. Эффект апельсиновой корки:
Эти эффекты (маркировка) появляются на металлах при растяжении.
Это также явление шероховатости поверхности, обычно наблюдаемое в крупнозернистых металлах при операциях формования при низкой температуре. Утончение зерна устраняет эти эффекты.
Теория Коттрелла о точках текучести :
Резкий предел текучести, наблюдаемый во многих металлах, является результатом теории Коттрелла, которая утверждает, что всегда существуют особые атмосферы для изменения взаимодействия между дислокациями и растворенными атомами (например,г., углерод, азот и др.). Такие атмосферы закрепляют дислокации, и для освобождения дислокации требуются более высокие напряжения. Значение этого напряжения должно соответствовать верхним пределам текучести. Свободные дислокации снижают предел текучести.
Сезонная трещина :Сезонное растрескивание — это дефект, который возникает, когда материалы, находящиеся под внутренним напряжением, подвергаются воздействию агрессивных сред, таких как промышленная атмосфера, аммиак, ртутный нитрат или морская вода. Сезонное растрескивание или коррозионное растрескивание под напряжением приводит к медленному или быстрому росту трещин в зависимости от окружающей среды.Трещины могут быть межкристаллитными, трансгранулярными или сочетанием того и другого.
На скорость коррозии под напряжением влияют следующие факторы:
(i) Уровень стресса,
(ii) Коррозионный агент,
(iii) Время и температура воздействия,
(iv) Структура металла,
(v) Величина пластической деформации и
(vi) Поведение защитной пленки и другие факторы.
Было выдвинуто несколько теорий для объяснения механизма сезонного растрескивания, но обычно считается, что это происходит из-за локальной электрохимической коррозии вдоль узкого пути, формируя локальные анодные области по отношению к более катодным областям поверхности металла.
Хотя все медные сплавы, по-видимому, подвержены сезонному растрескиванию, опасность возрастает с увеличением содержания цинка. Сезонное растрескивание часто происходит в патронной латуни, но редко в красной латуни и других медных сплавах с содержанием цинка менее 15 процентов.
Сезонное растрескивание обычно предотвращается / сводится к минимуму с помощью соответствующей обработки для снятия напряжения (отжига). Для латуни рекомендуемая температура отжига составляет 300 ° C.
Эффект Баушингера :Эффект Баушингера связан с реверсированием нагрузки или циклическим напряжением.Этот эффект был обнаружен Оханом Баушингером в 1886 году. При пластической деформации обычно наблюдается, что если кристаллические материалы, скажем, металлы, нагружаются сверх предела упругости, а нагрузка снимается и применяется повторно, предел текучести и пропорциональный предел материала увеличиваются. .
Но если напряжение приложено в противоположном направлении, пластическая деформация начинается с более низким пределом текучести, чем при начальной деформации. Это явление известно как эффект Баушингера (или упругий гистерезис).Это объясняется наличием остаточных напряжений, из-за которых дислокации легче перемещаются в направлении, противоположном исходному, вызывая деформацию при более низком значении напряжения.
На рис. 3.33 показано влияние изменения напряжения на кривую деформации. Степень эффекта Баушингера определяется LM под названием штамм Баушингера. Металлы, которые деформируются за счет двойникования, демонстрируют большую деформацию Баушингера.
Эффект Баушингера очень полезен при холодной обработке металлов.Например, холоднокатаная сталь упрочняется за счет применения принципа деформационного упрочнения. Пропуск стального прутка через ролики сжимает его в поперечном направлении и заставляет удлиняться. Относительное удлинение вызывает увеличение предела текучести при растяжении, но поперечное сжатие вызывает снижение предела текучести при растяжении по стержню.
Упругое последействие :Упругое последействие — это временная зависимость деформации от нагрузки и разгрузки материала. Рис. 3.34 иллюстрирует этот эффект на диаграмме линии деформации. Когда тело подвергается нагрузке, возникает мгновенная деформация (e 1 ), за которой следует замедленная упругая деформация (e 2 ) в течение определенного периода времени без какого-либо дальнейшего увеличения нагрузки.
Скорость этого увеличения уменьшается, и тело перестает деформироваться. При снятии нагрузки материал будет освобожден от начальной деформации e 1 , но будет иметь деформацию, равную e 2 , и со временем асимптотически вернется в исходное положение.Это явление известно как упругое последействие, которое часто также называют замедленной упругой деформацией, восстановлением ползучести или упругой памятью.
Упругое последействие частично вызвано медленным выделением тепла из-за напряжения и диффузии примесей в чистых материалах и частично из-за эффекта механического гистерезиса зерен.
Механизм, вызывающий упругое последействие, часто называют внутренним трением.
Было замечено, что от 25 до 90% общей деформации, в зависимости от материала, происходит из-за упругого последействия.
Термоупругий эффект:
Это своего рода упругое последействие. Когда член удлиняется, его объем увеличивается, что сопровождается падением его температуры. Это явление противоположно тепловому расширению. Если удлинение происходит достаточно медленно, чтобы поддерживать тепловое равновесие, поглощение тепла из окружающей среды поддерживает постоянную температуру элемента и процесс является изотермическим.
Если, с другой стороны, удлинение происходит быстро и времени для нагрева недостаточно, процесс является адиабатическим, и температура элемента понижается.Если над таким элементом напряжение остается постоянным и ему позволяют поглощать тепло, происходит дальнейшее расширение до тех пор, пока общее удлинение не станет таким же, как в изотермическом процессе. Эти два процесса показаны на рис. 3.35.
Изотермическое удлинение представлено линией OM, а адиабатическое удлинение — линией OL. Этот эффект очень мал и может быть обнаружен очень точными измерениями. Показанное расстояние LM сильно преувеличено для объяснения. Во время разгрузки проявляется аналогичное поведение; линия MO показывает изотермический путь разгрузки, тогда как ML показывает адиабатический путь.
Предпочтительная ориентация :Неслучайное расположение кристаллов или молекул известно как предпочтительная ориентация.
Ориентация зерен в отдельных кристаллах в металле обычно случайна. Холодная обработка, такая как прокатка, волочение проволоки и обжимка, разрушает эту хаотичность ориентации зерен, тем самым лишая поликристаллический материал равенства свойств во всех направлениях (изотропия).
Теперь зерно демонстрирует предпочтительную ориентацию, а свойства материала сильно различаются в разных направлениях (анизотропия).Предпочтительная ориентация возникает при пластической деформации и является результатом тенденции направлений скольжения в каждом зерне совмещаться с некоторым общим направлением деформации.
Рис. 3.36 (b) показывает предпочтительную ориентацию при механической работе.
Помимо того, что она получается обработкой металлов, предпочтительную ориентацию можно также увидеть в литых металлах, имеющих столбчатый рост.
На предпочтительную ориентацию обычно не влияют такие переменные обработки, как угол матрицы, скорость валков, обжатие за проход и т. Д.Направление потока — самая важная переменная процесса.
Предпочтительные ориентации определяют рентгеновскими методами.
Наиболее важным следствием предпочтительной ориентации зерен в металле является влияние на упругие свойства.
Наличие предпочтительной ориентации может привести к нежелательным последствиям. Прочность и связанные с ней свойства устройств, сформированных из таких материалов, отражают анизотропию отдельных кристаллитов, составляющих их.Например, когда круглые чашки штампуются из металлических листов, имеющих предпочтительную ориентацию, стороны получаемых чашек не ровные, что называется «колошением».
Поэтому во многих приложениях следует по возможности избегать предпочтительной ориентации. Иногда его можно удалить с металлов путем надлежащего отжига после обработки металла. И наоборот, возможно, что для некоторых приложений требуется наличие предпочтительной ориентации, например, легкость намагничивания кристалла зависит от кристаллографического направления, параллельного магнитному полю.В зависимости от желаемого конечного результата может потребоваться легкое или жесткое направление намагничивания, параллельное определенному направлению в конечном устройстве.
Несколько инженерных приложений для предпочтительной ориентации:
1. Предпочтительная ориентация усиливает намагничивание в кремнистых сталях, но нежелательна для других.
2. Это приводит к потере пластичности, особенно у полуфабрикатов, таких как листовой металл и проволока.
3. Еще одним важным применением контролируемой предпочтительной ориентации является производство металлических листов для сердечников трансформаторов. Предпочтительная ориентация железного сердечника в направлении магнитного поля позволяет сэкономить значительную электрическую энергию, рассеиваемую в виде тепла в железном сердечнике из-за вихревых токов.
4. Формирование сильной предпочтительной ориентации приведет к анизотропии механических свойств, то есть во время изготовления могут быть получены разные механические свойства в разных направлениях.
5. В литых металлах столбчатой формы.
Деформационное (или деформационное) упрочнение :Деформационное упрочнение — это явление, которое приводит к увеличению упрочнения и прочности металла (образца), подвергнутого пластической деформации при температуре ниже диапазона рекристаллизации (холодная обработка).
Когда материал подвергается пластической деформации, определенная работа, проделанная с ним, сохраняется внутри в виде энергии деформации.Эта дополнительная энергия в кристалле приводит к упрочнению или деформационному упрочнению твердых тел.
Таким образом, деформационное (или деформационное) упрочнение можно определить как повышенную твердость, сопровождающую пластическую деформацию. Это увеличение твердости сопровождается увеличением как предела прочности на разрыв, так и предела текучести.
Накладное упрочнение снижает пластичность и пластичность.
Накладное упрочнение используется во многих производственных процессах, таких как прокатка прутков и волочение труб.
Он также используется для повышения упругости при производстве многих деталей, таких как:
(i) Предварительное растяжение подъемных цепей и тросов,
(ii) Первоначальное создание давления в резервуаре высокого давления, цилиндрах гидравлического пресса и пистолетах.
Механизм рабочего упрочнения:
Деформационное упрочнение вызывается дислокациями, взаимодействующими друг с другом и с барьерами, препятствующими их движению через кристаллическую решетку. Упрочнение из-за взаимодействия дислокаций представляет собой сложную проблему, поскольку в ней участвуют большие группы дислокаций, и сложно определить групповое поведение простым математическим способом.
Одной из самых простых концепций дислокаций для объяснения деформационного упрочнения был идеал, согласно которому дислокации накапливаются на плоскостях скольжения на барьерах в кристалле.Скопления создают обратное напряжение, которое противостоит приложенному напряжению на плоскости скольжения.
Другой механизм деформационного упрочнения в дополнение к механизму из-за обратного напряжения, возникающего в результате скопления дислокаций на барьерах, как полагают, происходит, когда дислокации, движущиеся в плоскости скольжения, прорезают другие дислокации, пересекающие плоскость скольжения. Дислокации, проходящие через активную плоскость скольжения, часто называют дислокационным лесом, а этот процесс деформационного упрочнения называют пересечением леса дислокаций.
Теория деформационного упрочнения:
Согласно всем теориям (деформационного упрочнения) деформационное упрочнение происходит из-за повышенного сопротивления, которое испытывают дислокации при движении через решетку, когда металл подвергался холодной обработке / деформации. Основная идея, выдвинутая Тейлором в 1934 году, заключалась в том, что деформационное упрочнение происходит из-за того, что дислокации мешают друг другу. Таким образом, напряжение (τ), необходимое для перемещения дислокации в поле напряжений других окружающих ее дислокаций, должно иметь более высокое значение.
Извлечение, перекристаллизация и рост зерен :Деформированный металл по сравнению с недеформированным состоянием находится в неравновесном и термодинамически нестабильном состоянии. В дальнейшем в деформационно упрочненном металле происходят самопроизвольные процессы даже при комнатной температуре.
При значительном повышении температуры металл пытается достичь равновесия посредством следующих процессов:
(i) Восстановление,
(ii) перекристаллизация и
(iii) Рост зерна.
На рис. 3.37 показан схематический чертеж, показывающий восстановление, рекристаллизацию и рост зерен, а также изменения важных свойств в каждой области.
(i) Восстановление:
Это низкотемпературное явление, которое приводит к восстановлению физических свойств без каких-либо заметных изменений микроструктуры.
Во время восстановления на твердость оказывается незначительное влияние, тогда как электрическое сопротивление быстро уменьшается до значения после отжига.
Процесс восстановления важен для снятия внутренних напряжений в поковках, формованном и изготовленном оборудовании, гильзах картриджей и котельных трубах без снижения прочности, приобретаемой во время холодной обработки.
(ii) Перекристаллизация :
Это процесс, при котором деформированные зерна холоднодеформированного металла заменяются новыми зернами без деформации во время нагрева выше определенной минимальной температуры, называемой температурой рекристаллизации.
Температура рекристаллизации является функцией —
(i) Особый металл.
(ii) Чистота металла — Растворимые примеси повышают температуру перекристаллизации.
(iii) Металл / сплавы — Рекристаллизация обычно происходит при температуре около 0,3 T m для чистых металлов и около 0,5 T m для сплавов, где T m — температура плавления,
(iv) Величина предварительной деформации — Чем выше степень холодной обработки, тем ниже температура рекристаллизации и меньше размер зерна.
(v) Время отжига — Чем больше время отжига, тем ниже температура, необходимая для рекристаллизации.
(vi) Размер зерна — Чем мельче размер зерна холоднодеформированного металла, тем ниже температура рекристаллизации.
Процесс рекристаллизации можно разделить на три состояния —
(i) Зарождение зародышей.
(ii) Рост первичного зерна.
(iii) Вторичный рост зерна.
Во время зародышеобразования небольшие зародыши без деформации образуются в точках на границах кристаллических зерен в нагретой структуре.
При «росте первичного зерна» ядра превращаются в зерна до тех пор, пока они не встретятся впервые, заменяя старые зерна новыми, которые теперь свободны от деформаций и, в конечном итоге, «вторичный рост зерна», который сопровождается ростом новых зерен за счет других. и имеют небольшие размеры. При длительном нагревании при высокой температуре зерна быстро растут и дают локально увеличенный рост зерна.
(iii) Рост зерна:
Рост зерна — это увеличение размера зерна.
Когда материал выдерживают более длительное время при температуре выше температуры кристаллизации или когда он нагревается до более высокой температуры, размер зерна увеличивается, а твердость и прочность уменьшается, а пластичность увеличивается. Снижение твердости не такое резкое, как при рекристаллизации.
При данной температуре размер зерна D в данный момент времени определяется следующим соотношением, известным как закон размера зерна —
D 2 — D 2 0 = C.т
Где, D = размер зерна в данный момент времени, D 0 = исходный размер зерна, C = константа пропорциональности и t = время.
Процесс роста зерна во многом зависит от следующих факторов:
(i) Температура отжига.
(ii) Время отжига.
(iii) Скорость нагрева.
(iv) Степень предварительной деформации.
(v) Нерастворимые свойства.
(vi) Легирующие элементы.
Определение размера зерна:
При рассмотрении свойств поликристаллического материала часто определяется размер зерна.В связи с этим существует ряд методов, с помощью которых размер определяется в терминах среднего объема зерна, диаметра или площади.
Размер зерна можно оценить с помощью метода перехвата, описанного ниже:
(i) Прямые линии одинаковой длины, проведенные на нескольких микрофотографиях, показывают зернистую структуру.
(ii) Подсчитываются зерна, пересекаемые каждым отрезком линии.
(iii) Длина линии затем делится на среднее число пересеченных зерен, взятых по всем сегментам линии.
(iv) Средний диаметр зерна определяется делением этого результата на линейное увеличение микрофотографий.
Наиболее распространенный метод, вероятно, разработан Американским обществом испытаний и материалов (ASTM). ASTM подготовил несколько стандартных сравнительных таблиц, каждая из которых имеет различный средний размер зерна. Каждому из них присваивается номер в диапазоне от 1 до 10, который называется размером зерна, чем больше это число, тем меньше зерна.
Образец должен быть правильным размером 100 x. Размер зерна выражается как размер зерна на диаграмме, который наиболее близко соответствует зернам на микрофотографии. Таким образом, возможно относительно простое и удобное визуальное определение размера зерна.
Число зерен широко используется в спецификациях сталей.
Холодная деформация :Металл считается холодно обработанным, если он подвергается механической обработке при температуре ниже температуры рекристаллизации металла.
Холодная обработка обеспечивает улучшенную отделку поверхности и более точные допуски по размерам, и из-за этого характерные процессы холодной обработки обычно используются при производстве конечных продуктов.
Поскольку рекристаллизация не происходит при холодной обработке, зерна деформируются.
При холодной обработке возникают остаточные напряжения. Поскольку их присутствие нежелательно, обычно необходима подходящая термическая обработка для нейтрализации этих напряжений и восстановления исходной структуры металла.
Различные операции холодной обработки:
1. Чертеж
2. Выжимание
3. Гибка
4. Стрижка
5. Зубофрезерный
6. Дробеструйная обработка и
7. Холодное экструдирование.
При чрезмерной холодной обработке металл может расколоться, не достигнув желаемых форм и размеров, и во избежание этого операции холодной обработки проводятся в несколько этапов.
Горячая обработка :Когда пластическая деформация металла осуществляется при температуре выше температуры рекристаллизации, процессы, выполняемые с металлами, называются горячей обработкой.
Процесс горячей обработки можно рассматривать как одновременное сочетание холодной обработки и отжига. Любой эффект наклепа, вызванный пластической деформацией, немедленно нейтрализуется воздействием высокой температуры.
Процесс горячей обработки облегчает формовку металла с низким энергопотреблением, хотя обработка горячих материалов обходится дорого.
При горячей обработке происходит потеря металла из-за окалины, и точный допуск на размер не может быть достигнут.
Горячая обработка увеличивает плотность, так как любые поры или полости в литом металле исчезают.
Структура зерен становится более изысканной.
Различные операции горячей обработки:
1. Прокатный
2. Поковка
3. Сварка труб
4. Горячий пирсинг
5. Горячая обработка
6. Горячее прядение и
7. Горячее экструдирование.
Механизмы пластической деформации монокристаллов ГПУ с различной ориентацией: моделирование молекулярной динамики
Материалы (Базель).2021 фев; 14 (4): 733.
Юн Мао
2 Школа материалов и энергии, Юньнаньский университет, Куньмин 650091, Китай; nc.ude.uny@gnoyoam
Павел Лукач, академический редактор
2 Школа материалов и энергии, Юньнаньский университет, Куньмин 650091, Китай; nc.ude.uny@gnoyoamПоступила в редакцию 8 января 2021 г .; Принято 1 февраля 2021 г.
Лицензиат MDPI, Базель, Швейцария. Эта статья представляет собой статью в открытом доступе, распространяемую в соответствии с условиями лицензии Creative Commons Attribution (CC BY) (http: // creativecommons.org / licenses / by / 4.0 /).Abstract
Механизмы деформации монокристаллов Mg, Zr и Ti с различной ориентацией систематически изучаются с помощью молекулярно-динамического моделирования. Исследованы факторы, влияющие на пластичность гексагональных плотноупакованных (ГПУ) металлов. Результаты показывают, что базальная дислокация < a >, призматическая дислокация < a > и пирамидальная дислокация < c + a > активируются в монокристаллах Mg, Zr и Ti.Предыдущая система скольжения определяется комбинированным действием фактора Шмида и критических разрешенных касательных напряжений (CRSS). Двойникование играет решающую роль во время пластической деформации, поскольку базальное и призматическое скольжение ограничено. Двойникование 101¯2 обычно наблюдается в Mg, Zr и Ti из-за его низкого CRSS. Двойник 101¯1 появляется в Mg и Ti, но не в Zr из-за высокого CRSS. Вызванное напряжением фазовое превращение ГПУ-ГЦК происходит в Ti, что достигается последовательным скольжением частичных дислокаций Шокли по базисным плоскостям.В Ti активируется больше типов механизмов пластической деформации (включая поперечное скольжение, двойные двойники и фазовое превращение ГПУ-ГЦК), чем в Mg и Zr. Множественные механизмы деформации координируются друг с другом, что приводит к более высокой прочности и хорошей пластичности Ti. Результаты моделирования хорошо согласуются с соответствующими экспериментальными наблюдениями.
Ключевые слова: ГПУ-металлы, пластическая деформация, эффект ориентации, моделирование молекулярной динамики
1. Введение
Из-за низкой симметрии и ограниченного числа активированных систем скольжения гексагональные плотноупакованные (ГПУ) металлы деформируются. поведение, которое сильно отличается от поведения материалов с кубической кристаллической структурой.В ГПУ-металлах наиболее популярными механизмами пластической деформации являются скольжение и двойникование. В общем случае скольжение всегда происходит в направлении плотной упаковки решетки на плоскости плотной упаковки. Таким образом, в ГПУ-металлах система скольжения изменяется с изменением отношения c / a. Например, базальное скольжение < a > легче всего активируется в hcp Mg [1]. Однако призматическое скольжение < a > доминирует над пластичностью ГПУ Ti и Zr [2,3]. Под нагрузкой по оси c, когда базальное и призматическое скольжения ограничены, возможна активация пирамидальных скольжений < c + a > [4,5,6].
Двойникование обычно наблюдается в ГПУ-металлах. По сравнению с металлами с кубической кристаллической структурой, которые имеют ограниченное количество систем двойникования, в ГПУ-металлах существует по крайней мере семь мод двойникования, таких как 101¯1, 101¯2, 101¯3, 112¯1, 112¯2, 112¯ 3 и 112¯4, близнецы. Переориентация решетки, вызванная двойникованием, может обеспечить возможность активации большего количества систем скольжения, что может быть благоприятным для дальнейшей деформации. Факторы, влияющие на режимы двойникования, включают отношения c / a , плотности упаковки решетки, межплоскостные расстояния, энергии дефектов упаковки и так далее.В Mg и его сплавах двойник растяжения 101¯2 и двойник сжатия 101¯1 являются наиболее популярными режимами двойникования [7,8,9,10]. В Ti и его сплавах чаще всего наблюдаются двойники растяжения 101¯2 и 112¯1, а двойники сжатия — 112¯2 и 101¯1 [11,12,13,14]. Пластичность, индуцированная двойникованием (TWIP), была предложена для объяснения аномально высокой пластичности Ti при низкой температуре из-за богатой системы двойникования в Ti [15]. В Zr и его сплавах двойник растяжения 101¯2 чаще наблюдается, чем двойник 101¯2 [16], тогда как двойник 112¯2 преобладает при сжатии по оси c.При высоких температурах, 101¯1, двойник также активируется при сжатии в Zr [17,18]. Кроме того, при деформации ГПУ-металлов наблюдаются разные типы двойных двойников (ДД); например, 101¯1−101¯2. DT, в частности, связан с пластической деформацией и преждевременным разрушением сплавов Mg [19], в то время как двойники двойного сжатия (DCTW) 101¯1−101¯1 также были недавно исследованы в сплавах Mg [20]. 112¯1−112¯2 DT наблюдалось при более низких температурах в ГПУ Ti [21].
Помимо скольжения и двойникования важную роль в пластичности ГПУ-металлов играет фазовое превращение.Общеизвестно, что аллотропное превращение происходит при 882 ° C в чистом Ti из ГПУ ɑ-Ti в ОЦК β-Ti [22]. Кроме того, ГЦК-Ti наблюдалась в тонких пленках Ti [23] и в мультислоях Ni / Ti [24] и Al / Ti [25]. Соответствующие исследования показали, что фазовое превращение ГПУ-ГЦК в Ti вызвано приложенным напряжением, а не термической активацией [26]. Поверхностные и ориентационные эффекты на индуцированное напряжением фазовое превращение ГПУ-ГЦК в наностолбиках Ti также были недавно исследованы [27].Двухфазная фазовая граница HCP / FCC теоретически исследована с использованием классического молекулярно-динамического моделирования [28].
В целом ГПУ-металлы демонстрируют сильные анизотропные механические свойства из-за их асимметричной кристаллографической структуры. Эффект ориентации оказывает большое влияние на деформационное поведение такой асимметричной структуры [29,30,31,32]. При разных условиях нагружения могут активироваться разные механизмы деформации. В Mg и его сплавах проскальзывания < c + a > активируются, когда базовое скольжение ограничено, и различные двойники растяжения и сжатия появляются отдельно под растяжением и сжатием по оси c.Используя молекулярно-динамическое моделирование, Zu et al. В [29] сообщалось об ориентационном эффекте на начальную пластическую деформацию монокристаллов Mg, обсуждался механизм конкуренции различных пластических деформаций при различных условиях нагружения. В поликристаллическом Zr влияние ориентации на микромеханические характеристики было изучено с помощью сферического наноиндентирования Pathak et al. [30]. Battaini et al. [31] сообщили об эффекте ориентации на механическое поведение пластины из чистого титана, и напряжение течения сильно варьировалось из-за ориентации образца.
Из-за сложности механизмов деформации в ГПУ-металлах выяснение факторов, влияющих на прочность и пластичность, имеет большое значение для улучшения механических свойств ГПУ-материалов. В этой статье моделирование молекулярной динамики используется для исследования механизмов деформации различных монокристаллов ГПУ, таких как Mg, Zr и Ti, с различными отношениями c / a при различных условиях нагружения. Сравнивая механизмы деформации различных ГПУ-металлов и анализируя влияние ориентации на деформационное поведение, дополнительно обсуждаются факторы, влияющие на пластичность ГПУ-металлов.
2. Метод моделирования
Для изучения механизмов пластической деформации при различных условиях нагружения созданы две модели монокристалла (A и B) с разной ориентацией. показаны идеальные модели монокристаллов с квадратным поперечным сечением. Длина стороны образцов составляет около 14,3 нм, а отношение высоты к длине стороны составляет около 2: 1. Число атомов в системах около 280 000. Свободные граничные условия применяются в направлениях x и z, в то время как граничное условие с фиксированным смещением назначается для направления y.Направление загрузки всегда по оси y. В a мы ориентируем направление 12¯10 как ось x, направление 0001 как ось y и направление 1¯010 как ось z для исходной структуры. Затем кристалл поворачивается вокруг оси 1¯010 от 0 ° до 90 °, что означает, что угол (θ) между направлением нагрузки (y) и осью c находится в диапазоне от 0 ° до 90 °. Оси b, x, y и z соответственно параллельны направлениям 1¯010, 0001 и 12¯10 в исходной структуре. Затем кристалл поворачивается вокруг оси 12¯10 от 0 ° до 90 °.Угол (β) между направлением нагрузки (y) и осью c составлял от 0 ° до 90 °. Десять различных углов θ 0 °, 10 °, 15 °, 32,1 °, 43,3 °, 51,6 °, 70 °, 75 °, 80 °, 90 ° и двенадцать различных углов β 0 °, 10 °, 15 °, 28,6 °, 35,9 °, 47,4 °, 55,4 °, 58,6 °, 70 °, 75 °, 80 °, 90 ° рассматриваются в нашем моделировании. Моделирование выполняется в постоянном ансамбле NVT с интегратором Верле скорости. Температуру поддерживают на уровне 5 К. Потенциалы ЕАМ Sun et al. для Mg [33], Менделев и Экланд (Массачусетс) для Zr [34], Ackland et al.для Ti [35]. Метод расчета по умолчанию в программе LAMMPS [36], который основан на классической статистической механике [37,38], и теорема вириала [39] применяется для расчета напряжения. Программа AtomEye [40] используется для визуализации эволюции атомистических структур. Кристаллические дефекты окрашены с помощью анализа Экланда [41] и анализа общих соседей (CNA) [42].
Имитационные модели. ( a ) модель A и ( b ) модель B. Ось y указывает направление нагрузки.
Сначала идеальный кристалл расслабляется в течение 30 пс (5000 временных шагов) при нулевой силе, чтобы минимизировать потенциальную энергию. Затем прикладывают одноосное растяжение в направлении y с постоянной скоростью деформации около 5 · 107 с-1 на верхнем слое толщиной 1,5 нм, в то время как нижний слой толщиной 1,5 нм фиксируется. Система расслабляется в течение 6 пс, прежде чем будет применено следующее приращение смещения при растяжении. Максимальная деформация, полученная в нашем моделировании, составляет около 10%.
3. Результаты и обсуждение
3.1. Первоначальные механизмы пластической деформации Mg, Zr и Ti
Пластическая деформация монокристаллов Mg, Zr и Ti при одноосном растяжении с различной ориентацией показана на и. Указаны начальные механизмы пластической деформации в интервале деформаций 0,2% от предела текучести. Дислокация, кристаллографическая переориентация и фазовое превращение ГПУ-ГЦК обозначены как или, синим и зеленым, соответственно. Механизмы дислокации включают базальную дислокацию < a > (BD < a >), призматическую дислокацию < a > (PrD < a >), пирамидальную дислокацию < c + a > (PyD < c + a >), полосу сдвига (SB), базальный дефект упаковки (BSF) и поперечное скольжение призматической и пирамидальной < a > дислокации.Кристаллографическая переориентация включает двойникование и базально-призматическое (БП) преобразование. Наблюдается несколько мод двойникования, включая двойников 101¯1 и 101¯2, двойных двойников 101¯1−101¯2 и 112¯1−112¯2. Видно, что типов механизмов пластической деформации в Ti больше, чем в Mg и Zr. В Ti .Мы представим детали различных механизмов пластической деформации в монокристаллах Mg, Zr и Ti в следующих разделах.
Таблица 1
Механизмы пластической деформации монокристаллов ГПУ при растяжении с различной ориентацией (θ).
| θ (°) | Mg [26] (c / a = 1,623) | Zr ( c / a = 1,593) | Ti ( c / a = 1,588) |
|---|---|---|---|
| 0 ( c -ось) | PyD < c + a >, BD < a >, BSF, T3, BP | PyD < c + a >, BD < a >, BSF, T3, BP | T3, BP, BSF, fcc-Ti |
| 10 | SB | PyD < c + a >, SB | PyD < c + a >, SB |
| 15 | SB | PyD < c + a >, SB | BD < a >, BSF, PyD < c + a >, SB, DT |
| 32.1 | SB | BD < a >, BSF | BD < a >, BSF |
| 43,3 | PrD < a >, BD < a >, BSF | PrD < a >, BD < a >, BSF | BD < a >, BSF |
| 51,6 | PrD < a >, BD < a >, BSF | PrD < a >, BD < a >, BSF | BD < a >, BSF |
| 70 | PrD < a >, T1, BSF, BP, GB | PrD < a > | PrD < a >, PyD < a >, Т1, BSF, fcc-Ti |
| 75 | PrD < a >, T1, BSF, BP, GB | PrD < a > | PrD < a >, PyD < a >, Т1, BSF, fcc-Ti |
| 80 | T1, BSF, BP, ГБ | PrD < a > | PrD < a >, PyD < a >, Т1, BSF, fcc-Ti |
| 90 | T1, BSF, BP, ГБ | PrD < a > | PrD < a >, PyD < a >, Т1, BSF, fcc-Ti |
Таблица 2
Механизмы пластической деформации монокристаллов ГПУ при растяжении с различной ориентацией (β).
| β (°) | Mg ( c / a = 1,623) | Zr ( c / a = 1,593) | Ti ( c / a = 1,588 ) |
|---|---|---|---|
| 0 ( c -ось) | PyD < c + a >, BD < a >, BSF, T3, BP | PyD < c + a >, BD < a >, BSF, T3, BP | T3, BP, BSF, fcc-Ti |
| 10 | BD < a >, BSF, PyD < c + a >, SB | PyD < c + a >, SB | BD < a >, BSF, PyD < c + a >, SB, DT |
| 15 | BD < a >, BSF, PyD < c + a >, SB | PyD < c + a >, BD < a >, BSF | BD < a >, BSF, fcc-Ti |
| 28.6 | BD < a >, BSF | PyD < c + a >, BD < a >, BSF | BD < a >, BSF, fcc-Ti |
| 35,9 | BD < a >, BSF | PyD < c + a >, BD < a >, BSF | PyD < c + a >, fcc-Ti, BP |
| 47,4 | BD < a >, BSF | BD < a >, BSF, PrD < a >, PyD < c + a > | BD < a >, BSF, fcc-Ti |
| 55.4 | BD < a >, BSF | BD < a >, BSF, PrD < a >, PyD < c + a > | BD < a >, BSF, fcc-Ti |
| 58,6 | BD < a >, BSF | BD < a >, BSF, PrD < a >, PyD < c + a > | BD < a >, BSF, fcc-Ti |
| 70 | Т1, BSF, BP, ГБ | PyD < c + a >, PrD < a > | PrD < a >, BD < a >, BSF |
| 75 | PrD < a >, Т1, BSF | PyD < c + a >, PrD < a > | PrD < a >, BD < a >, BSF |
| 80 | PrD < a >, Т1, BSF | PyD < c + a >, PrD < a > | PrD < a > |
| 90 | PrD < a >, Т1, BSF | PyD < c + a >, PrD < a > | PrD < a > |
3.2. Скольжения
В ГПУ-металлах преобладающим направлением скольжения всегда является направление плотной упаковки решетки 12¯10. Предпочтительной плоскостью скольжения в Mg является базисная плоскость, в то время как предпочтительной плоскостью скольжения в Ti и Zr является плоскость призмы. Выбор активированных режимов скольжения в ГПУ-металлах, подверженных приложенному напряжению, зависит от фактора Шмида и критического разрешенного напряжения сдвига (CRSS) в соответствии с законом Шмида. и представить коэффициенты Шмида для четырех систем скольжения в Mg, Zr и Ti, когда натяжение идет вдоль направления с разными θ или β.Предполагается, что система скольжения с большим фактором Шмида будет преимущественно активироваться во время деформации. Как показано на фиг. И, когда натяжение прикладывается по оси c , пирамидальные дислокации < c + a > предпочтительны, поскольку факторы Шмида базального и призматического скольжения равны нулю. С увеличением θ или β фактор Шмида базального скольжения становится больше, таким образом, базальные скольжения постепенно доминируют над начальной пластической деформацией. Когда θ или β приближается к 90 °, призматическое скольжение < a > предпочтительнее, чем базальное скольжение < a > в соответствии с фактором Шмида, поэтому призматические дислокации < a > являются основным механизмом пластической деформации, когда θ ≥ 70 °.
Таблица 3
Коэффициенты Шмида (f) систем скольжения для монокристалла ГПУ с различными θ.
| Направление нагрузки (θ) | BD < a > | PrD < a > | PyD < c + a > 101¯1 〈1123¯〉 | PyD < c + a > (SB) 12¯11 〈112¯6〉 | ||||
|---|---|---|---|---|---|---|---|---|
| Mg | Zr | Ti | Mg | Zr | Ti | |||
| 0 | 0 | 0 | 0.401 | 0,404 | 0,404 | 0,281 | 0,286 | 0,286 |
| 15 | 0,25 | 0,029 | 0,493 | 0,493 | 0,493 | 0,451 | 0,453 | 0,454 |
| 32,1 | 0,450 | 0,122 | 0,468 | 0.466 | 0,466 | 0,495 | 0,494 | 0,493 |
| 51,6 | 0,487 | 0,266 | 0,288 | 0,284 | 0,283 | 0,469 | 0,464 | 0,464 |
| 70 | 0,321 | 0,382 | 0,436 | 0,435 | 0,434 | 0,481 | 0,480 | 0.484 |
| 90 | 0 | 0,433 | 0,400 | 0,405 | 0,405 | 0,282 | 0,286 | 0,287 |
Таблица 4
Коэффициенты Шмида (f) систем скольжения для монокристаллов ГПУ с различными β.
| Направление нагрузки (β) | BD < a > | PrD < a > | PyD < c + a > 101¯1 〈1123¯〉 | PyD < c + a > (SB) 12¯11 〈112¯6〉 | ||||
|---|---|---|---|---|---|---|---|---|
| Mg | Zr | Ti | Mg | Zr | Ti | |||
| 0 | 0 | 0 | 0.401 | 0,404 | 0,404 | 0,281 | 0,286 | 0,286 |
| 10 | 0,125 | 0,013 | 0,469 | 0,470 | 0,470 | 0,388 | 0,388 | 0,392 |
| 28,6 | 0,365 | 0,099 | 0,442 | 0,440 | 0.438 | 0,470 | 0,470 | 0,472 |
| 55,4 | 0,399 | 0,293 | 0,394 | 0,389 | 0,390 | 0,388 | 0,386 | 0,387 |
| 70 | 0,278 | 0,382 | 0,480 | 0,479 | 0,477 | 0,383 | 0,383 | 0,386 |
| 90 | 0 | 0.433 | 0,401 | 0,405 | 0,405 | 0,211 | 0,214 | 0,216 |
показывает пластическую деформацию монокристалла Zr с различной ориентацией (θ). а показывает результаты при θ = 15 °. Атомы на идеальной ГПУ решетке не показаны. При приложенной деформации до 5,75% зарождается преимущественно пирамидальная дислокация 101¯1 (f = 0,493) ((a1)). С увеличением деформации появляется СП, вызванная пирамидальным скольжением 12¯11 (f = 0.453) ((а2)). В этой пирамидальной СБ происходит переориентация решетки с углом поворота 34 °, а угол поворота совпадает с углом разориентации двойника 12¯11. Этот режим деформации обычно определялся как двойник типа II 12¯11 в предыдущих работах [43,44]. Подробный анализ SB был применен в Mg Zu et al. [29], что совпадает с результатами этого моделирования.
Атомные конфигурации Zr при ( a ) θ = 15 °, ( b ) θ = 32.1 °, ( c ) θ = 90 °.
При θ до 32,1 ° базальная дислокация < a > доминирует над исходной пластичностью Zr. Как показано на (b1), ведущая дислокация в базисной плоскости зарождается на свободной поверхности, а за ней следует замыкающая дислокация. Между тем между передней и задней частичными дислокациями существует ЧСФ. В (b2) задняя дислокация догоняет ведущую, чтобы заполнить базальную дислокацию < a >. Затем базальная дислокация < a > движется дальше и распространяется на свободную поверхность, оставляя ступеньку скольжения на поверхности ((b3)).Снимки в (c1, c2) представляют собой деформацию Zr при θ = 90 °, когда деформации составляют 5,62% и 5,86% соответственно. Когда деформация растяжения составляет 5,62%, в первую очередь активируется призматическое скольжение < a > (f = 0,433) ((c1)). С увеличением деформации новые призматические дислокации < a > последовательно зарождаются и распространяются по образцу ((c2)).
В b, базальная дислокация < a > диссоциирует на частички Шокли на базисной плоскости. Однако идеальная призматическая дислокация < a > может существовать без каких-либо обширных дефектов упаковки (SF), возникающих в c.Ключевыми факторами, определяющими режим скольжения дислокации, являются напряжение Пайерлса и энергия дефектов упаковки (ЭДУ). В Zr и Ti скольжение призматической дислокации имеет минимальное напряжение Пайерлса [45,46], что указывает на то, что полную призматическую дислокацию < a > легче активировать, чем дислокации в другой плоскости. Величина SFE определяет легкость разделения на частичные. Базальную дислокацию легче разделить на частичные из-за ее более низкой ЭДУ [47]. Поэтому обычно наблюдается диссоциация базальной дислокации < a > на две частичные и BSF.
Результаты моделирования монокристаллов Mg в первую очередь согласуются с результатами моделирования Zr для модели A, тогда как результаты моделирования монокристалла Ti несколько отличаются при θ ≥ 70 °. Призматические дислокации < a > в Ti могут поперечно скользить в пересекающуюся пирамидальную плоскость. Активация системы вторичного скольжения полезна для достижения полной трехмерной деформации, которая также способствует зарождению последующих 101¯1 двойников (подробности будут обсуждаться в разделе 3.3.2). Подобное поперечное скольжение дислокаций < a > в Ti также наблюдалось Caillard et al. [48].
Мы замечаем, что при β = 10 ° фактор Шмида пирамидального скольжения 101¯1 〈112¯3〉 (f ~ 0,470) намного выше, чем у базального скольжения < a > (f = 0,125 ) в Mg и Ti. Однако базальное скольжение < a > происходит раньше пирамидального скольжения < c + a > из-за более высокого CRSS для скольжения < c + a > при низких температурах.CRSS — это параметр материала, который зависит от температуры деформации, скорости деформации, примесей и т. Д. Chapuis et al. обнаружили, что при температуре 298 K для Mg значения CRSS составляют 5 МПа для базального скольжения < a > и 110 МПа для пирамидального скольжения первого порядка < c + a > [49]. Он показал, что значение CRSS для пирамидального скольжения < c + a > примерно в 22 раза больше, чем для базального скольжения < a >. Таким образом, базальное скольжение активировать легче, чем пирамидальное.
В наших расчетах, за исключением SBs, вызванных пирамидальным скольжением 112¯1, в Mg наблюдается только 101¯1 пирамидальное скольжение. Это отличается от экспериментального наблюдения, что пирамидальное скольжение 112¯2 доминирует над пластичностью в Mg. Tang et al. [50] объяснили это расхождение между экспериментом и моделированием. При моделировании молекулярной динамики они наблюдали 101¯1 пирамидальную дислокацию < c + a > первой во время нагружения по оси c путем последовательного зарождения ведущих и замыкающих частичных дислокаций.Впоследствии образование 112¯2 пирамидальных дислокаций достигается либо за счет поперечного скольжения винтовых сегментов, либо за счет совместного скольжения краевых сегментов по двум равным и альтернативным 101¯1 пирамидальным плоскостям. Далее скольжение происходит преимущественно на пирамидальных плоскостях 112¯2, что согласуется с экспериментами. Wu et al. также объяснил это явление с точки зрения энергетики дислокационных превращений [48]. Разница энергий между дислокациями < c + a > на плоскостях 101¯1 и 112¯2 в Mg мала, что указывает на относительно легкое поперечное скольжение.Но для Zr и Ti энергетически предпочтительнее дислокация < c + a > на пирамидальной плоскости 101¯1. Следовательно, скольжение < c + a > должно преобладать на пирамидальной плоскости 101¯1, и поперечное скольжение затруднено из-за большой разницы энергий. Однако некоторые эксперименты показывают поперечное скольжение 112¯2 пирамидальных < c + a > дислокаций в Ti и его сплавах [51,52], особенно при сжатии по оси c при высоких температурах.В этих экспериментах активация пирамидального скольжения 112¯2 и поперечного скольжения может быть связана с напряжением, температурой, легированием твердого раствора или их комбинацией.
3.3. Двойникование
Двойникование — это основная форма деформации в ГПУ-металлах. Чаще всего наблюдаются четыре режима двойникования, в том числе два двойника растяжения 101¯2 〈1¯011〉 и 112¯1 〈1¯1¯26〉, два двойника сжатия 112¯2 〈112¯3〉 и 101¯1 〈112¯ 3〉. В нашем моделировании 101¯2 двойника появляются в Mg, Zr и Ti при осевом растяжении c .101¯1 двойник наблюдается в Mg и Ti. 12¯11 двойники (ДБ) типа II появляются в Mg, Zr и Ti. Кроме того, 101¯1−101¯2 двойных двойников Mg и 112¯1−112¯2 двойных двойников Ti обнаружены в нескольких направлениях нагружения.
3.3.1. 101¯2 Двойникование
Из и показано, что двойники 101¯2 наблюдаются при θ = 0 ° ( c растяжение по оси) для Mg, Zr и Ti. CRSS двойников 101¯2 в Mg, Zr и Ti составляют 30 МПа, 165 МПа и 260 МПа соответственно [49,53,54], что меньше, чем у других двойников.Следовательно, двойники 101¯2 более активны в ГПУ-металлах, особенно в Mg. Двойникование 101¯2 широко наблюдалось с помощью экспериментов и атомистического моделирования, а механизм двойникования 101¯2 широко обсуждался [7,8,10,11,16]. показывает исходную пластичность монокристалла Zr при осевом растяжении c . Сначала возникает пирамидальная дислокация < c + a >, затем следует базальное скольжение (a, b). При последующей деформации переориентированный кристалл из-за трансформации БП и двойникования 101¯2 пересекает образец и расширяется к концу кристалла (c, d).Превращение БП и двойникование 101¯2 доминируют в пластичности Zr при θ = 0 °. e, f представляет увеличенный вид террасной границы раздела, которая состоит из интерфейсов BP, 101¯2 границ когерентного двойникования (CTBs) и интерфейсных дефектов. На границе обнаружены двухслойные двойниковые дислокации (b2CTB), двухслойные разрывы БП (b2BP) и однослойные разрывы БП (b1BP). Рост переориентированного кристалла достигается за счет миграции CTBs и BP интерфейсов через перемещение интерфейсных дефектов, сопровождающееся преобразованием между 101¯2 CTB и BP интерфейсом.Механизм деформации монокристалла Zr при растяжении по оси c в этом моделировании почти такой же, как у монокристалла Mg, полученного Zu et al. [29].
( a — d ) Атомные конфигурации Zr при θ = 0 °. ( e , f ) Конфигурации увеличенного атома террасного интерфейса состоят из 101¯2 интерфейсов CTB и BP вместе с дефектами интерфейса.
Для монокристалла Ti при напряжении по оси c ситуация несколько отличается от ситуации с Mg и Zr.Как показано на рисунке a, двойник 101¯2 зарождается непосредственно на свободной поверхности, при этом первичные дислокации не наблюдаются. Когда напряжение увеличивается, двойная область продолжает расширяться (б). Затем BSF испускаются на границе раздела BP (c), что вызвало образование fcc-Ti в d. Образование ГЦК-Ti индуцируется накоплением BSF, что согласуется с анализом Li et al. [55]. e – h показывает зарождение и рост двойника 101¯2 на разных временных шагах, если смотреть вдоль направления 12¯10.Двойник 101¯2 зарождается на свободной поверхности в монокристалле Ti (e). Интерфейсы BP возникают в результате преобразования CTB (f). Затем интерфейсы BP перемещаются через одно- и двухуровневые отключения (g, h).
( a — d ) Атомные конфигурации Ti при θ = 0 °. ( e — h ) Процесс зарождения и роста двойника 101¯2 в направлении 12¯10.
3.3.2. 101¯1 Двойникование
Двойники сжатия 101¯1 наблюдаются, когда θ или β ≥ 70 ° для Mg и θ ≥ 70 ° для Ti.CRSS двойника 101¯1 в Mg, Zr и Ti составляют 55 МПа, 300 МПа и 360 МПа соответственно [49,53,54]. Таким образом, 101¯1. близнецы легче всего образуются в Mg. Двойник 101¯1 в Zr не наблюдается из-за более высокого CRSS. Многие исследователи сообщили, что близнецы 101¯1 могут образовываться только при повышенных температурах в Zr [17,18]. Для Ti зарождение 101¯1 двойников обычно связывают с поперечным скольжением дислокаций [13].
Чтобы понять механизмы зарождения и роста двойника 101¯1, описывается эволюция микроструктуры образца Mg и Ti при θ или β ≥ 70 °.представлена пластическая деформация Ti при θ = 80 °. При деформации до 6,3% (a) поперечное скольжение призматической < a > и пирамидальной < a > дислокации происходит на свободной поверхности. Между тем, зародыш-близнец 101¯1 формируется за счет расширения 101¯1 пирамидальной < a > дислокации. В 2016 году Серра и др. предложил механизм зародышеобразования для 101¯1 двойника с помощью атомистического моделирования. Было показано, что при диссоциации винтовой дислокации < a > может трансформироваться зародыш-двойник [13].Kou et al. наблюдали в реальном времени процесс двойникования 101¯1 на вершине трещины Ti с помощью просвечивающего электронного микроскопа (ПЭМ) [14]. Двойник зародыша возникает в результате скольжения по плоскости 101¯1 испускаемых решеточных дислокаций. При деформации 6,34% на b наблюдаются как двойник 101¯1, так и BSF, и ГЦК-Ti. На увеличенном изображении d, e можно заметить, что внутри 101¯1 близнеца появляется обильный BSF. Из-за взаимодействия BSF с границей двойников 101¯1 (TB) на TB остаются однослойные сидячие ступеньки (b 1 ).Kou et al. показали, что сидячие ступеньки могут действовать как стабильные источники зарождения двойниковых дислокаций b 2 , в то время как двойникование 101¯1 осуществляется за счет скольжения b 2 [14]. Более того, накопление BSF вызовет образование fcc-Ti, как показано на d.
( a — c ) Атомные конфигурации Ti при θ = 80 °. ( d , e ) Увеличенное изображение дефектов.
a показывает пластическую деформацию Mg при β = 70 °.Зародыш-близнец 101¯1 зарождается непосредственно на свободной поверхности, когда деформация составляет 5,48% ((a1)). Они распространяются с увеличением деформации, что сопровождается образованием BSF. При деформации до 5,56% трансформация БП происходит внутри области двойников 101¯1, и наблюдается двойная двойниковая кристаллическая переориентация 101¯1−101¯2 ((a2)). Эта двойная двойниковая кристаллическая переориентация была описана Zu et al. [56] в 2018 году, что согласуется с результатом этого моделирования.б представляет деформацию Mg при β = 90 °. На (b1) призматическая дислокация зарождается на поверхности сначала при деформации 5,93%. Впоследствии зародыш-двойник 101¯1 зарождается на пересечении призматической дислокации и свободной поверхности. Когда деформация увеличивается до 5,94%, BSF обнаруживается в области двойников, как отмечено на (b2).
Атомные конфигурации Mg при ( a ) β = 70 °, ( b ) β = 90 °.
Зарождение двойников 101¯1, вызванное многократным скольжением дислокаций < a >, наблюдается при моделировании образцов Mg и Ti на рисунках и b.В частности, двойники 101¯1 могут зарождаться непосредственно на свободной поверхности в Mg при нескольких условиях нагружения, что связано с меньшим значением CRSS двойника 101¯1 для Mg (65 МПа). Следует отметить, что BSF обычно наблюдаются внутри двойников 101¯1 в Mg и Ti. Оба конца BSF связаны с двойниковыми границами, и BSF растут с миграцией TB. Несколько экспериментов и моделирования показали существование BSF с высокой плотностью внутри 101¯1 двойников [20,57,58], включая структуру иерархического сжатия нанодвойников и дефектов упаковки (CTWSFs), описанную Peng et al.в 2019 году [20]. Наши расчеты показывают, что факторы Шмида BSF внутри области двойников 101¯1 больше, чем в матрице, которые больше или равны 0,402 при θ или β ≥ 70 °. Таким образом, BSF образуются у 101¯1 двойника из-за высокого фактора Шмида. BSFs внутри близнецов, как ожидается, будут играть ту же роль, что и TB, в препятствовании смещению дислокаций [58].
3.4. Двойные двойники (DT)
В нашем моделировании наблюдаются два типа DT: 101¯1−101¯2 DT в Mg при θ ≥ 70 ° и β = 70 °, 112¯1−112¯2 DT в Ti при θ = 15 ° и β = 10 °.
101¯1−101¯2 DT в Mg при β = 70 ° показано на (a2), что согласуется с переориентацией двойного двойникового кристалла 101¯1−101¯2, описанной Zu et al. [56]. После зарождения первичного двойника 101¯1 следует вторичный двойник 101¯2, объединяющий первичный двойник в стабильную структуру 101¯1−101¯2 DT. Типичная структура границ зерен (GB) идентифицируется между родительским и вторичным двойником. В частности, интерфейс между первичным двойником 101¯1 и вторичным двойником 101¯2 имеет зигзагообразный вид, состоящий из сосуществующих 101¯2 TB и интерфейса BP ((a2)).Эта двойная двойниковая переориентация кристалла 101¯1−101¯2 также наблюдается в Mg при θ ≥ 70 °, что совпадает с переориентацией β = 70 °.
Кроме того, 101¯1−101¯2 DT в Mg наблюдаются под напряжением растяжения вблизи a -ось, 112¯1−112¯2 DT в Ti наблюдаются при θ = 15 ° и β = 10 ° под напряжение растяжения около c — ось. ДТ 112¯1−112¯2 наблюдались Gong et al. с помощью просвечивающего электронного микроскопа высокого разрешения (HRTEM) [59]. представляет начальную пластическую деформацию Ti при θ = 15 °.В a базовая дислокация < a > зарождается сначала на свободной поверхности, затем следуют пирамидальные дислокации 101¯1 〈112¯3〉. С увеличением деформации SB растет (б) и распространяется по образцу (в) за счет движения пирамидальных частичных дислокаций 1¯21¯1. После этого двойник 112¯2 зарождается на пересечении границы раздела 1¯21¯1 и свободной поверхности, и образуется двойной двойник 112¯1−112¯2 (d). Согласно геометрическому анализу в e, фактор Шмида двойника 112¯2 внутри двойника 112¯1 (f = 0.305) больше значения в матрице (f = 0,282) при θ = 15 °. Следовательно, вторичный двойник 112¯2 формируется из-за более высокого фактора Шмида и сосредоточенного напряжения на пересечении границы 112¯1 и свободной поверхности. При β = 10 ° 101¯1−101¯2 DT также наблюдается в Ti. Предпочтительные режимы вторичного двойникования в ГПУ-металлах будут ослаблять локальную концентрацию напряжений и деформаций, связанных с первичной областью.
( a — d ) Атомные конфигурации Ti при θ = 15 °.( e ) Геометрический анализ 112¯1−112¯2 DT.
3.5. Фазовое превращение
Фазовое превращение, вызванное напряжением, в Mg и Zr трудно происходить при низких температурах. В монокристаллах Ti фазовый переход от ГПУ к ГЦК структуре наблюдается при θ = 0 °, θ ≥ 70 ° и β = 15–58,6 °. В нашем моделировании фазовое превращение ГПУ-ГЦК осуществляется посредством последовательного скольжения базальных частичных дислокаций, что наблюдалось в предыдущих исследованиях [28,54,60].
Как показано на d, ГЦК-Ti наблюдается при θ = 0 ° из-за накопления BSF. представляет детали преобразования ГПУ-ГЦК. Террасный интерфейс показан в a, который состоит из интерфейсов БП, 101¯2 ТБ и межфазных дефектов. Обнаружены два типа межфазных разъединений в интерфейсе BP, обозначенные как двухуровневые шаги и однослойные шаги. На рисунке b базальные частичные дислокации излучаются в межфазных разъединениях и расширяются к свободной поверхности с оставленными BSF.В c, ГЦК-Ti образуется из-за последовательной эмиссии базальных частичных дислокаций и накопления BSF. Указывается, что ориентационное соотношение между ГПУ и ГЦК фазами составляет {0001} ГПУ || {111} ГЦК и 〈112¯0〉 ГПУ || 〈110〉 ГЦК . Преобразование ГПУ-ГЦК, вызванное накоплением BSF, также наблюдается внутри двойника 101¯1, как показано на d.
( a — c ) преобразование ГЦК-Ti при θ = 0 °.
При β = 35.9 ° (a) наблюдается ГЦК-Ti, индуцированный накоплением BSF, связанный с диссоциацией 101¯1 частичной дислокации ((a1)). С увеличением деформации поверхность раздела БП и ПБ появляются вблизи ГЦК-Ti ((a2)). Когда β = 58,6 ° (b), ГЦК-Ti зарождается непосредственно на свободной поверхности из-за более высокого фактора Шмида базального скольжения, который также индуцируется накоплением BSF.
ПревращениеГЦК-Ti при ( a ) β = 35.9 ° и ( b ) β = 58.6 °.
4. Обсуждение
Как мы знаем, механизмы пластической деформации Mg, Zr и Ti заметно отличаются друг от друга. Он тесно связан с кристаллической структурой, разнообразием соотношений c, /, и т. Д. CRSS связан с кристаллической структурой, которая описывает критическое напряжение для пластической деформации, возникающей в данном режиме деформации. Различные металлы имеют разные значения CRSS для одной данной системы скольжения или режима двойникования.Мы можем проанализировать легкость или сложность активации одного режима деформации, сравнивая значения CRSS различных металлов. Базальное скольжение < a > предпочтительнее для Mg, в то время как призменное скольжение < a > предпочтительнее для Ti и Zr, которые определяются соотношением c / a и отражаются в величине значений CRSS. . Базальная дислокация < a > имеет гораздо более низкое значение CRSS (5 МПа), чем у других систем скольжения (> 90 МПа) в Mg [49].Призматическая дислокация < a > является наиболее активным дефектом с минимальным значением для Zr (15 МПа) и Ti (60 МПа) [53,54]. CRSS двойника 101¯2 в Mg (30 МПа) также намного ниже, чем у Zr (165 МПа) и Ti (260 МПа) [49,53,54]. Более низкие CRSS скольжения и двойникования в Mg приводят к тому, что прочность Mg намного ниже, чем у Ti и Zr. Более того, в Ti можно одновременно активировать больше типов механизмов пластической деформации, включая поперечное скольжение, сплетение и фазовое превращение, что приводит к повышению прочности и пластичности Ti и его сплавов.
Из-за асимметричной кристаллографической структуры и анизотропии эффект ориентации очень важен для деформации ГПУ-металлов. Когда нагрузка прикладывается в другом направлении, предел текучести довольно изменчив, как из-за низкой симметрии и систем ограниченного скольжения ГПУ-металлов. Коэффициенты Шмида используются для анализа эффекта ориентации, который определяется направлениями нагрузки и соотношением c / . Для данного механизма деформации коэффициенты Шмида для разных ГПУ-металлов (Mg, Zr или Ti) имеют крошечную разницу.Система скольжения с большим фактором Шмида имеет приоритет для активации во время деформации. Как правило, всесторонний анализ факторов Шмида и CRSS скольжения почти совпадает с последствиями механизма деформации в нашем моделировании. Например, базальное скольжение < a > происходит до пирамидального скольжения < c + a >, когда β = 10 ° в Mg и Ti, хотя фактор Шмида 101¯1 〈112¯3 〉 Пирамидальное скольжение (f ~ 0,470) намного выше, чем у базального скольжения < a > (f = 0.125). Это связано с более высоким CRSS для скольжения < c + a >, чем для базального скольжения < a > при низких температурах. Комбинированный эффект CRSS и фактора Шмида определяет ранее активированную систему скольжения. Более того, когда нагрузка прикладывается вблизи базисной плоскости, двойники 101¯1 образуются в Mg и Ti из-за более высоких факторов Шмида. Но в нашем моделировании двойник 101¯1 не появляется в Zr. Это разумно, поскольку Zr имеет высокое значение CRSS 101¯1 двойник при низких температурах.Многие исследователи сообщили, что двойник 101¯1 может образоваться только при повышенных температурах в Zr [17,18].
На основе систематического анализа механизмов деформации в ГПУ-металлах обсуждаются факторы, влияющие на пластичность ГПУ-материалов. Согласно приведенному выше анализу, для улучшения механических свойств материалов с ГПУ можно применить несколько методов. Сначала легирование некоторыми элементами могло бы привести к изменению CRSS различных мод деформации по сравнению с чистыми ГПУ-металлами.Многие исследователи наблюдали эффект легирования CRSS в ГПУ-металлах. Qian et al. сообщили, что добавление Li к Mg увеличивает CRSS для базального скольжения, в то время как CRSS для призменного скольжения снижается [61]. Ojha et al. обсудили влияние содержания Nb и Ta на CRSS для скольжения, двойникования и фазового превращения в сплавах на основе Ti [62]. Westlake et al. предположили, что CRSS Zr был увеличен на 500% за счет добавления H в виде тонкодисперсных игл гидрида [63].Помимо CRSS, кристаллографическая текстура, связанная с эффектом ориентации, может эффективно влиять на механизмы деформации. Например, формирование базовой текстуры, а также уменьшение размера зерен может повысить формуемость Mg [64]. Sattari et al. выдвинули предположение, что кристаллографическая текстура напорной трубы играет ключевую роль в ее внутриреакторном поведении, таком как ползучесть и рост облучения [65]. Предыдущее исследование показало, что микротекстура имеет сильное влияние как на продвижение, так и на подавление роста полосы адиабатического сдвига в ГПУ-металлах, а контроль микротекстуры может открыть возможность для новых сплавов с более высокой ударной вязкостью [66].
5. Выводы
Механизмы пластической деформации монокристаллов Mg, Zr и Ti с различной ориентацией систематически исследуются с помощью моделирования молекулярной динамики. Для образцов с разной ориентацией с θ или β в диапазоне от 0 ° до 90 ° проявляются разные механизмы пластической деформации. Сравнивая механизмы деформации различных ГПУ-металлов и анализируя влияние ориентации на поведение деформации, анализируются факторы, влияющие на пластичность ГПУ-металлов.
(1)
Шликеры определяют пластичность монокристаллов ГПУ. Базальное скольжение предпочтительнее для Mg, тогда как призменное скольжение предпочтительнее для Ti и Zr, которые характеризуются соотношением c / a и значениями CRSS. Механизмы скольжения, наблюдаемые в нашем моделировании, хорошо согласуются с комплексным анализом фактора Шмида и CRSS систем скольжения.
(2)
Когда базальное и призматическое скольжения ограничены, активируется двойникование. Двойникование 101¯2 обычно наблюдается в монокристаллах Mg, Zr и Ti из-за его низкого CRSS, которое обычно сопровождается превращением BP.Двойники 101¯1 образуются в Mg и Ti, но не в Zr. Двойники 12¯11 типа II (SB) появляются в Mg, Zr и Ti. Кроме того, наблюдаются DT 101¯1−101¯2 в Mg и 112¯1−112¯2 DT в Ti, ответственные за релаксацию локальных напряжений и концентрацию деформаций, связанных с первичным двойником.
(3)
Наблюдается индуцированный напряжением фазовый переход из ГПУ в ГЦК структуру в Ti, который достигается за счет накопления BSF. Для образцов с различной ориентацией ГЦК-фаза может зарождаться на дефектах или на свободной поверхности за счет активации и последовательного скольжения базальных частичных дислокаций.
(4)
Более низкие CRSS скольжения и двойникования в Mg приводят к тому, что прочность Mg намного ниже, чем у Ti и Zr. Более того, в Ti больше типов механизмов пластической деформации, чем в Mg и Zr. Множественные механизмы деформации координируются друг с другом, что приводит к высокой прочности и пластичности Ti.
На основе всестороннего анализа механизмов деформации монокристаллов с ГПУ обсуждаются механизмы упрочнения материалов с ГПУ.Легирование элементами может привести к изменению CRSS по сравнению с чистыми ГПУ-металлами, что приведет к улучшению механических свойств. Более того, технология обработки, связанная с эффектом ориентации, может эффективно влиять на механизмы деформации, которые могут быть реализованы для разработки новых материалов с ГПУ.
Вклад авторов
Концептуализация, Z.-C.M .; расследование, Z.-C.M .; методология, З.-К.М. и X.-Z.T .; программное обеспечение, Z.-C.M. и X.-Z.T .; администрация проекта, Ю.-Ф.Г. и Y.M .; надзор, Ю.-Ф.Г. и Y.M .; письменность — черновик, З.-ЦМ .; написание — просмотр и редактирование, Ю.-Ф.Г. Все авторы прочитали и согласились с опубликованной версией рукописи.
Финансирование
Эта работа была поддержана Национальным фондом естественных наук Китая (№№ 11772043 и 11972071) и крупным научно-технологическим проектом генной инженерии материалов из драгоценных металлов в провинции Юньнань (№ 2019ZE001-1, 202002AB080001, 2018IC058) .
Заявление институционального наблюдательного совета
Не применимо.
Заявление об информированном согласии
Не применимо.
Заявление о доступности данных
Данные содержатся в статье.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Сноски
Примечание издателя: MDPI остается нейтральным в отношении юрисдикционных претензий на опубликованных картах и филиалов организаций.
