Катушка на схеме: Катушка индуктивности. Обозначение на схеме и примеры её использования в электронике.

Содержание

Катушка индуктивности. Обозначение на схеме и примеры её использования в электронике.

Обозначение, параметры и разновидности катушек индуктивности

Одним из самых известных и необходимых элементов аналоговых радиотехнических схем является катушка индуктивности. В цифровых электронных схемах индуктивные элементы практически потеряли свою актуальность и применяются только в устройствах питания как сглаживающие фильтры.

Катушки индуктивности на принципиальных схемах обозначаются латинской буквой “L” и имеют следующее изображение.

Разновидностей катушек индуктивности существуют десятки. Они бывают высокочастотные, низкочастотные, с подстроечными сердечниками и без них. Бывают катушки с отводами, катушки, рассчитанные на большие напряжения. Вот так, например, выглядят бескаркасные катушки.

Катушки для СВЧ аппаратуры называются микрополосковыми линиями. Они даже внешне не похожи на катушки. С катушками индуктивности связан такой эффект как резонанс и гениальный Никола Тесла получал на резонансных трансформаторах миллионы вольт.

Основной параметр катушки это её индуктивность. Величина индуктивности измеряется в Генри (Гн, англ. – «H»). Это достаточно большая величина и поэтому на практике применяют меньшие значения (мГн, mH – миллигенри и мкГн, μH– микрогенри) соответственно 10^-3 и 10^-6 Генри. Величина индуктивности катушки указывается рядом с её условным изображением (например, 100 μH). Чтобы не запутаться в микрогенри и миллигенри, советую узнать, что такое сокращённая запись численных величин.

Многие факторы влияют на индуктивность катушки. Это и диаметр провода, и число витков, а на высоких частотах, когда применяют бескаркасные катушки с небольшим числом витков, то индуктивность изменяют, сближая или раздвигая соседние витки.

Часто для увеличения индуктивности внутрь каркаса вводят сердечник из ферромагнетика, а для уменьшения индуктивности сердечник должен быть латунным.

То есть можно получить нужную индуктивность не увеличением числа витков, что ведёт к увеличению сопротивления, а использовать катушку с меньшим числом витков, но использовать ферритовый сердечник. Катушка индуктивности с сердечником изображается на схемах следующим образом.

В реальности катушка с сердечником может выглядеть так.

Также можно встретить катушки индуктивности с подстроечным сердечником. Изображаются они вот так.

Катушка с подстроечным сердечником вживую выглядит так.

Такая катушка, как правило, имеет сердечник, положение которого можно регулировать в небольших пределах. При этом величина индуктивности также меняется. Подстроечные катушки индуктивности применяются в устройствах, где требуется одноразовая подстройка. В дальнейшем индуктивность не регулируют.

Наряду с подстроечными катушками можно встретить и катушки с регулируемой индуктивностью. На схемах такие катушки обозначаются вот так.

В отличие от подстроечных катушек, регулируемые катушки индуктивности допускают многократную регулировку положения сердечника, а, следовательно, и индуктивности.

Ещё один параметр, который встречается достаточно часто это добротность контура. Под добротностью понимается отношение между реактивным и активным сопротивлением катушки индуктивности. Добротность обычно бывает в пределах 15 – 350.

На основе катушки индуктивности и конденсатора выполнен самый необходимый узел радиотехнических устройств, колебательный контур. На схеме изображён входной контур простого радиоприёмника рассчитанного на работу в диапазонах средних и длинных волн.

В настоящее время в этих диапазонах станций практически нет. Катушка индуктивности L1 имеет достаточно большое число витков, чтобы перекрыть диапазон по максимуму. Для улучшения приёма к первой обмотке L1 подключается внешняя антенна. Это может быть простой кусок проволоки длиной в пределах двух метров.

Благодаря большому числу витков в индуктивности L1 присутствует целый спектр частот и как минимум пять — шесть работающих радиостанций. Две индуктивности L1 и L2 намотанные на одном каркасе представляют собой высокочастотный трансформатор. Для того чтобы выделить на катушке индуктивности L2 станцию, работающую, допустим на частоте 650 КГц необходимо с помощью переменного конденсатора C1 настроить колебательный контур на данную частоту.

После этого выделенный сигнал можно подавать на базу транзистора усилителя высокой частоты. Это одно из применений катушки индуктивности. Точно на таком же принципе построены выходные каскады радио- и телевизионных передатчиков только наоборот. Антенна не принимает слабый сигнал, а отдаёт в пространство ЭДС.

Примеров использования катушки индуктивности великое множество. На рисунке изображён весьма несложный, но хорошо зарекомендовавший себя в работе сетевой фильтр.

Фильтр состоит из двух дросселей (катушек индуктивности) L1 и L2 и двух конденсаторов С1 и С2. на старых схемах дроссели могут обозначаться как Др1 и Др2. Сейчас это редкость. Катушки индуктивности намотаны проводом ПЭЛ-0,5 – 1,5 мм. на каркасе диаметром 5 миллиметров и содержат по 30 витков каждая. Очень хорошо параллельно сети 220V подключить варистор. Тогда защита от бросков сетевого напряжения будет практически полной. В качестве конденсаторов лучше не использовать керамические, а поискать старые, но надёжные МБМ на напряжение не менее 400V.

Вот так выглядит дроссель входного фильтра компьютероного блока питания ATX.

Как видно, он намотан на кольцеобразном сердечнике. На схеме он обозначается следующим образом. Точками отмечены места начала намотки провода. Это бывает важно, так как это влият на направление магнитного потока.

Выходные выпрямители современного импульсного блока питания всегда конструируют по двухполупериодным схемам. Широко известный выпрямительный диодный мост, у которого большие потери практически не используют. В двухполупериодных выпрямителях используют сборки из двух диодов Шоттки. Самая важная особенность выпрямителей в импульсных блоках питания это фильтры, которые начинаются с дросселя (индуктивности).

Напряжение, снимаемое с выхода выпрямителя обладающего индуктивным фильтром, зависит кроме амплитуды ещё и от скважности импульсов, поэтому очень легко регулировать выходное напряжение, регулируя скважность входного.

Процесс регулирования скважности импульсов называют широтно-импульсной модуляцией (ШИМ), а в качестве управляющей микросхемы используют ШИМ контроллер.

Поскольку амплитуда напряжения на входах всех выпрямителей изменяется одинаково, то стабилизируя одно напряжение, ШИМ контроллер стабилизирует все. Для увеличения эффекта, дроссели всех фильтров намотаны на общем магнитопроводе.

Именно таким образом устроены выходные цепи компьютерного блока питания формата AT и ATX. На его печатной плате легко обнаружить дроссель с общим магнитопроводом. Вот так он выглядит на плате.

Как уже говорилось, этот дроссель не только фильтрует высокочастотные помехи, но и играет важную роль в стабилизации выходных напряжений +12, -12, +5, -5. Если выпаять этот дроссель из схемы, то блок питания будет работать, но вот выходные напряжения будут «гулять» причём в очень больших пределах – проверено на практике.

Так магнитопровод у такого дросселя общий, а катушки индуктивности электрически не связаны, то на схемах такой дроссель обозначают так.

Здесь цифра после точки (L1.1; L1.2 и т.д.) указывает на порядковый номер катушки на принципиальной схеме.

Ещё одно очень хорошо известное применение катушки индуктивности это использование её в системах зажигания транспортных средств. Здесь катушка индуктивности работает как импульсный трансформатор. Она преобразует напряжение 12V с аккумулятора в высокое напряжение порядка нескольких десятков тысяч вольт, которого достаточно для образования искры в свече зажигания.

Когда через первичную обмотку катушки зажигания протекает ток, катушка запасает энергию в своём магнитном поле. При прекращении прохождения тока в первичной обмотке пропадающее магнитное поле индуцирует во вторичной обмотке мощный короткий импульс напряжением 25 – 35 киловольт.

Импульсный трансформатор из тех же катушек индуктивности является основным узлом хорошо известного устройства для самообороны как электорошокер. Схем может быть несколько, но принцип один: преобразование низкого напряжения от небольшой батарейки или аккумулятора в импульс слабого тока, но очень высокого напряжения.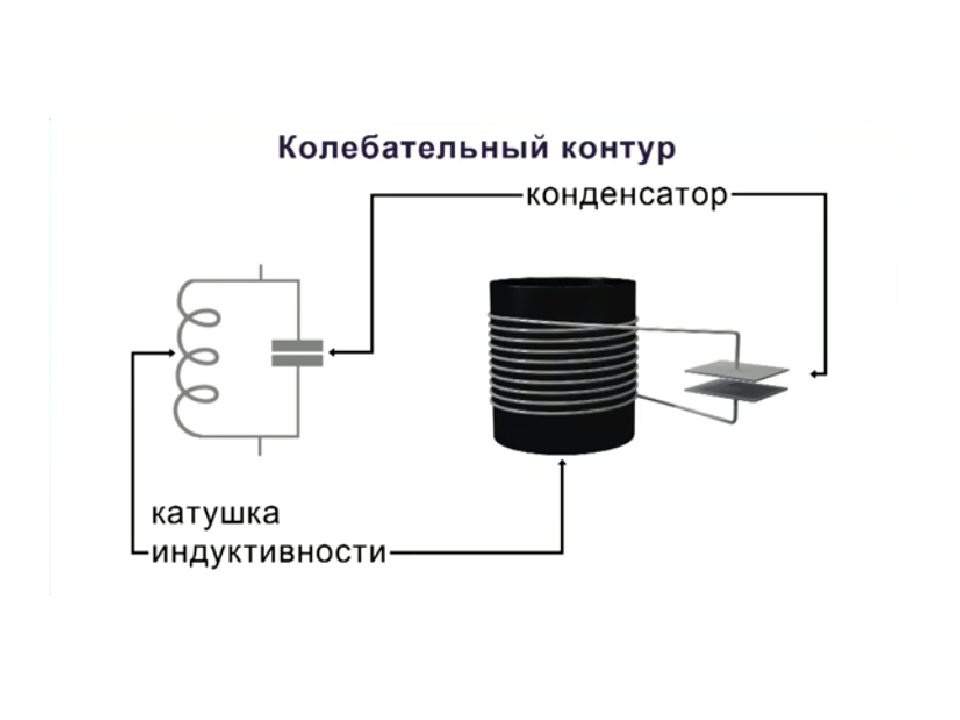 У серьёзных моделей напряжение может достигать 75 – 80 киловольт.

Главная &raquo Радиоэлектроника для начинающих &raquo Текущая страница

Также Вам будет интересно узнать:

Катушка индуктивности. Параметры. Виды. Обозначение на схемах

Здравствуйте, уважаемые читатели сайта sesaga.ru. Катушка индуктивности относится к числу элементов, без которых не получится построить приемник, телевизор, радиоуправляемую модель, передатчик, генератор сигналов, модемный преобразователь, сетевой фильтр и т.п.

Катушку индуктивности или просто катушку можно представить в виде нескольких витков провода намотанного в спираль. Ток проходя по каждому витку спирали создает в них магнитное поле, которое пересекаясь с соседними витками наводит в них э.д.с самоиндукции. И чем провод длиннее и большее число витков он образует, тем самоиндукция больше.

Индуктивность

По своей сути индуктивность является электрической инерцией и ее основное свойство состоит в том, чтобы оказывать сопротивление всякому изменению протекающего тока. Если через катушку пропускать определенный ток, то ее индуктивность будет противодействовать как уменьшению, так и увеличению протекающего тока.

В отличие от конденсатора, который пропускает переменный и не пропускает постоянный ток, катушка индуктивности свободно пропускает постоянный ток и оказывает сопротивление переменному току, потому что он изменяется быстрее, чем может изменяться магнитное поле.

И чем больше индуктивность катушки и чем выше частота тока, тем оказываемое сопротивление сильнее. Это свойство катушки применяют, например, в приемной аппаратуре, когда требуется в электрической цепи преградить путь переменному току.

Индуктивность измеряется в генри (Гн), миллигенри (1мГн = 10ˉ3 Гн), микрогенри (1мкГн = 10ˉ6 Гн), наногенри (1нГн = 10ˉ9 Гн) и обозначается латинской буквой L.

Общие свойства катушек индуктивности

В зависимости от требуемой индуктивности и частоты, на которой катушка будет работать, она может иметь самые различные исполнения.

Для высоких частот это может быть простая катушка состоящая из нескольких витков провода или же катушка с сердечником из ферромагнитного материала и иметь индуктивность от нескольких наногенри до нескольких десятков миллигенри. Такие катушки применяются в радиоприемной, передающей, измерительной аппаратуре и т.п.

Катушки, работающие на высоких частотах, можно разделить на катушки контуров, катушки связи и дроссели высокой частоты. В свою очередь катушки контуров могут быть с постоянной индуктивностью и переменной индуктивностью (вариометры).

По конструктивному признаку высокочастотные катушки разделяются на однослойные и многослойные, экранированные и неэкранированные, катушки без сердечников и катушки с магнитными и немагнитными сердечниками, бескаркасные, цилиндрические плоские и печатные.

Для работы в цепи переменного тока низкой частоты, на звуковых частотах, во входных фильтрах блоков питания, в цепях питания осветительного электрооборудования применяются катушки с достаточно большой индуктивностью.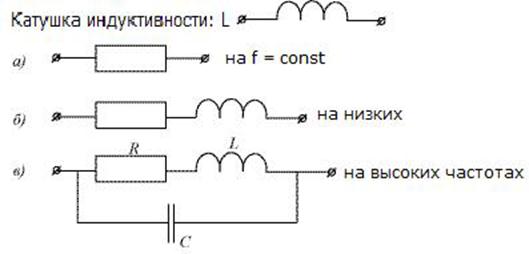 Их индуктивность достигает десятки и даже сотни генри, а в обмотках могут создаваться большие напряжения и протекать значительные токи.

Для увеличения индуктивности при изготовлении таких катушек применяют магнитопроводы (сердечники), собранные из отдельных тонких изолированных пластин сделанных из специальных магнитных материалов – электротехнических сталей, пермаллоев и др.

Применение наборных магнитопроводов обусловлено тем, что под действием переменного магнитного поля в сплошном магнитопроводе, который можно рассматривать как множество короткозамкнутых витков, образуются вихревые токи, которые нагревают магнитопровод, бесполезно потребляя часть энергии магнитного поля. Изоляция же между слоями стали оказывается на пути вихревых токов и значительно снижает потери.

Катушки с магнитопроводами из изолированных пластин можно разделить на дроссели и трансформаторы.

Основные параметры катушек индуктивности

Свойства катушек могут быть охарактеризованы четырьмя основными параметрами: индуктивностью, добротностью, собственной емкостью и стабильностью.

1. Индуктивность.

Индуктивность (коэффициент самоиндукции) является основным электрическим параметром и характеризует величину энергии, запасаемой катушкой при протекании по ней электрического тока. Чем больше индуктивность катушки, тем больше энергии она запасает в своем магнитном поле.

Индуктивность зависит от размеров каркаса, формы, числа витков катушки, диаметра и марки провода, а также от формы и материала магнитопровода (сердечника).

В радиолюбительских схемах, как правило, величину индуктивности не указывают, так как радиолюбителя интересует не эта величина, а количество витков провода в катушке, диаметр и марка провода, способ намотки (внавал, виток к витку, крест на крест, секционная намотка) и размеры каркаса катушки.

2. Добротность.

Добротность (Q) характеризуется качеством работы катушки индуктивности в цепях переменного тока и определяется как отношение реактивного сопротивления катушки к ее активному сопротивлению потерь.

Активное сопротивление включает в себя сопротивление провода обмотки катушки; сопротивление, вносимое диэлектрическими потерями в каркасе; сопротивление, вносимое собственной емкостью и сопротивления, вносимые потери в экраны и сердечники.

Чем меньше активное сопротивление, тем выше добротность катушки и ее качество. В большинстве случаев добротность катушки определяют резонансные свойства и к.п.д. контура.
Современные катушки средних размеров имеют добротность около 50 – 300.

3. Собственная емкость.

Катушки индуктивности обладают собственной емкостью, которая увеличивается по мере увеличения числа витков и размеров катушки. Между соседними витками существует межвитковая емкость, из-за которой некоторая часть тока проходит не по проводу, а через емкость между витками, отчего сопротивление между выводами катушки уменьшается.

Все дело в том, что общее напряжение, приложенное к катушке, разделяется на межвитковые напряжения из-за чего между витками образуется электрическое поле, вызывающее скопление зарядов.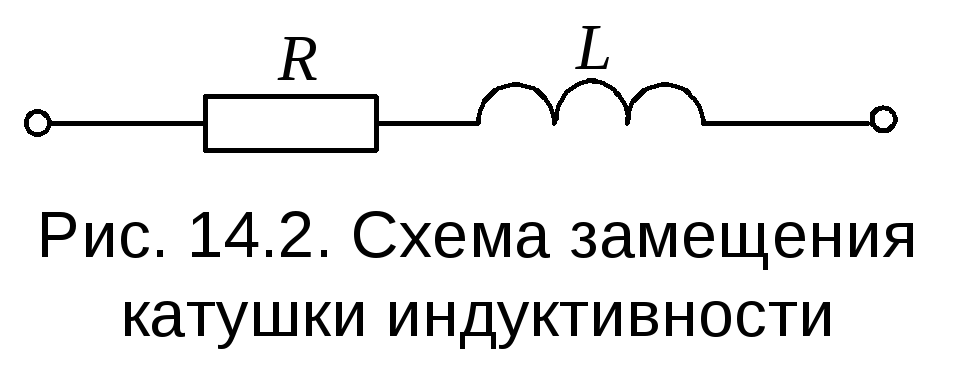 Витки, разделенные слоями изоляции, образуют обкладки множества маленьких конденсаторов, через которые протекает часть тока, из общей емкости которых и складывается собственная емкость катушки. Таким образом катушка обладает не только индуктивными но и емкостными свойствами.

Собственная емкость является вредным параметром и ее стремятся уменьшить применением специальных форм каркаса и способом намотки провода.

4. Стабильность.

Стабильность катушки характеризуется изменением ее параметров под воздействием температуры, влажности и во времени.

Изменение индуктивности под влиянием температуры характеризуют температурным коэффициентом индуктивности (ТКИ), равным относительному изменению индуктивности при изменении температуры на 1°С. ТКИ катушки определяется способом намотки и качеством диэлектрика каркаса.

Влажность вызывает увеличение собственной емкости и диэлектрических потерь, а также понижает стабильность катушки. Для защиты от действия влажности применяется герметизация или пропитка и обволакивание обмотки негигроскопичными составами.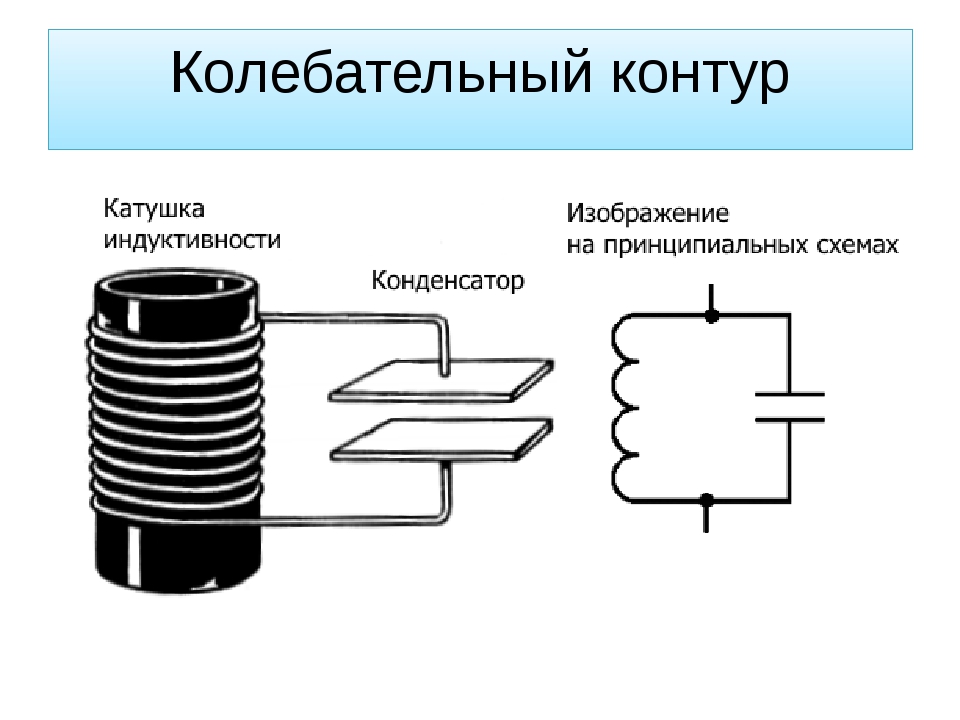

Такие катушки обладают более низкой добротностью и большой собственной емкостью, но при этом они более устойчивы к воздействию влаги.

Катушки индуктивности с магнитопроводами

Для получения малогабаритных катушек различного назначения применяют магнитопроводы (сердечники), которые изготавливают из магнитодиэлектриков и ферритов. Катушки с магнитопроводами имеют меньшее число витков при заданной индуктивности, малую длину провода и небольшие размеры.

Ценным свойством катушек с магнитопроводами является возможность их подстройки, т.е. изменения индуктивности в небольших пределах путем перемещения внутри катушки специального цилиндрического подстроечника, состоящего из феррита с напрессованной на него резьбовой втулкой.

Магнитодиэлектрики представляют собой измельченное вещество, содержащее в своем составе железо (ферромагнетик), частицы которого равномерно распределены в массе диэлектрика (бакелита или аминопласта). Наиболее широко применяют магнитопроводы из альсифера (сплав алюминия, кремния и железа) и карбонильного железа.

Ферриты представляют собой твердые растворы окислов металлов или их солей, прошедшие специальную термическую обработку (обжиг). Получающееся при этом вещество – полупроводниковая керамика – обладает очень хорошими магнитными свойствами и малыми потерями даже на очень высоких частотах.

Основным достоинством ферритов является высокая магнитная проницаемость, которая позволяет существенно уменьшить размеры катушек.

В старых принципиальных схемах магнитопроводы из магнитодиэлектриков и ферритов обозначались одинаково – утолщенной штриховой линией (рис. а). Впоследствии стандарт ЕСКД оставил этот символ для магнитопроводов из магнитодиэлектрика, а для ферритовых ввел обозначение, ранее применявшееся только для магнитопроводов низкочастотных дросселей и трансформаторов – сплошную жирую линию (рис. б). Однако согласно последней редакции ГОСТ 2.723.68 (март 1983г.) магнитопроводы катушек изображают линиями нормальной толщины (рис. в).

Катушки, индуктивность которых можно изменять с помощью магнитопровода, на электрических схемах указываются при помощи знака подстроечного регулирования, который вводится в ее условное обозначение.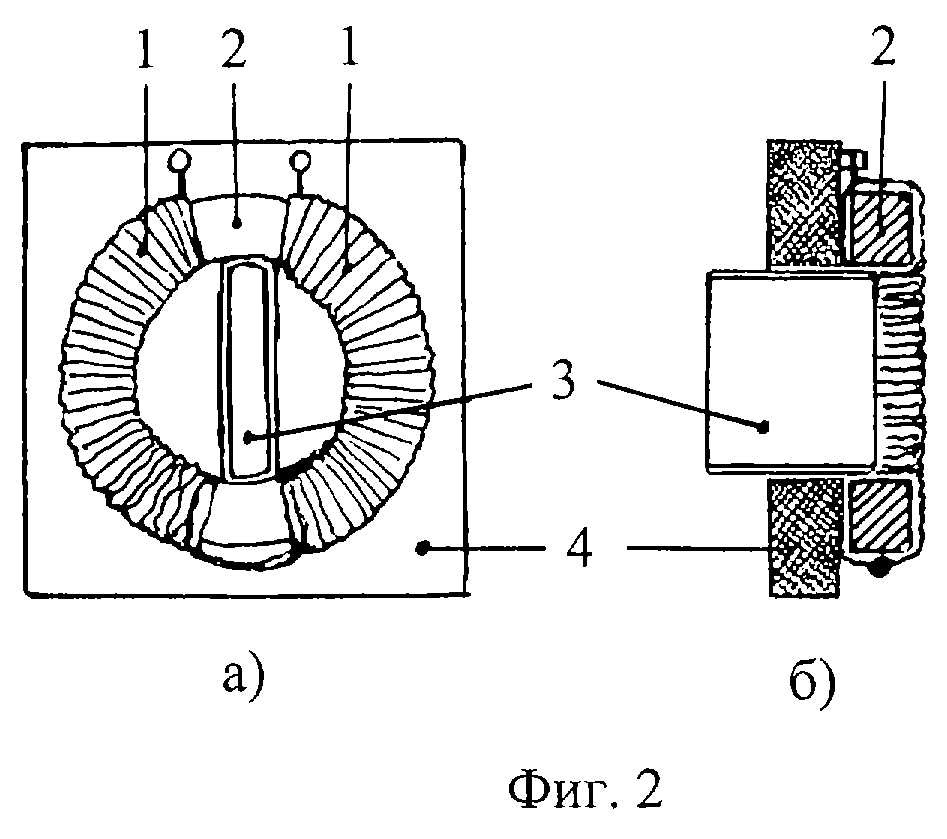

Изменение индуктивности обозначают двумя способами: либо знаком подстроечного регулирования пересекающим обозначения катушки и магнитопровода (рис. а), либо только пересечением магнитопровода с изображением его над катушкой (рис. б).

Экранированные катушки индуктивности

Для устранения паразитных связей, обусловленных внешним электромагнитным полем катушки и влияния на катушку окружающего пространства, ее экранируют, т.е. помещают в замкнутом металлическом экране.

Однако под влиянием экрана изменяются основные электрические параметры катушки: уменьшаются индуктивность и добротность, увеличивается сопротивление и собственная емкость.

Изменение параметров катушки тем больше, чем ближе к ее виткам расположен экран, т.е. изменение параметров зависит от соотношения между размерами катушки и размерами самого экрана.

Для высокочастотных катушек экраны выполняются в виде круглых или прямоугольных стаканов из алюминия, меди или латуни с толщиной стенок 0,3 – 0,5 мм.

Чтобы на схемах обозначить экранированную катушку, ее условное обозначение помещают в знак экранирования, который соединяют с корпусом.

Также необходимо отметить, что экранировать необходимо лишь катушки большого размера, диаметр которых составляет более 15 – 20 мм.

Катушки диаметром не более 4 – 5 мм создают магнитное поле в относительно небольшом пространстве и при удалении таких катушек от других деталей на расстояние в 4 – 5 раз больше их диаметра опасных связей, как правило, не возникает, поэтому они не нуждаются в специальном экранировании.

Обозначение катушек с отводами и начала обмотки

В радио и электротехнической аппаратуре, например, в приемниках или импульсных преобразователях напряжения, иногда используют не всю индуктивность катушки, а только некоторую ее часть. Для таких случаев катушки изготавливают с отводом или отводами.

При разработке некоторых конструкций иногда необходимо строго соблюсти начало и конец обмотки катушки или трансформатора. Чтобы указать, какой из концов обмотки является началом, а какой – концом, у вывода начала обмотки ставят жирную точку.

Для подстройки катушек на частотах свыше 15…20 МГц часто применяют магнитопроводы из немагнитных материалов (меди, алюминия и т.п.). Возникающие в таком магнитопроводе под действием магнитного поля катушки вихревые токи создают свое поле, противодействующее основному, в результате чего индуктивность катушки уменьшается.

Немагнитный магнитопровод-подстроечник обозначают так же, как и ферритовый, но рядом указывают химический символ металла, из которого он изготовлен. На рисунке изображен подстроечник, изготовленный из меди.

Вот и все, что хотел рассказать о катушках индуктивности.
Удачи!

Литература:
1. В. А. Волгов «Детали и узлы радиоэлектронной аппаратуры».
2. В. В. Фролов «Язык радиосхем».
3. М. А. Сгут «Условные обозначения и радиосхемы».

4. Катушки, дроссели, трансформаторы — Условные графические обозначения на электрических схемах — Компоненты — Инструкции

Независимо от реальной конструкции катушки индуктивности и дроссели изображают на схемах, как показано на рис. 4.1 [3].

Число полуокружностей в условном графическом обозначении катушек и дросселей может быть любым. Чаще количество полуокружностей выбирают равным четырем или же в зависимости от удобства их сопряжения на принципиальных схемах с символами других элементов (конденсаторов, резисторов и т. п.). В зависимости от конфигурации принципиальной схемы выводы обмотки направляют либо в одну сторону (рис. 4.1, L3), либо в разные (L1, L2, L4). Если необходимо показать отвод, то линию электрической связи присоединяют в месте сочленения полуокружностей или в середине одной из них (L4), причём точка не ставится.

Буквенно-цифровое позиционное обозначение катушек и дросселей состоит из буквы L и порядкового номера по схеме. Рядом (сверху или справа) можно указывать индуктивность, обычно в миллигенри или микрогенри.

Если катушка или дроссель имеет магнитопровод, условное графическое обозначение дополняют его символом — отрезком сплошной или прерывистой линии, располагаемым с «наружной» стороны полуокружностей (рис. 4.2). При этом магнитопроводы из карбонильного железа, альсифера или других магнитодиэлектриков изображают штриховой линией (L1), из феррита или ферромагнитного сплава (электротехническая сталь, пермаллой) — сплошной линией (L2). Магнитопроводы из немагнитных материалов (меди, алюминия и др.) обозначают так же, как и ферромагнитные, но рядом с УГО указывают химический символ металла.

Возможность подстройки индуктивности изменением положения магнитопровода показывают на схемах знаком подстроенного регулирования, пересекающим условное графическое обозначение катушки под углом 45° (рис. 4.2, L5, L6). Если необходимо обратить внимание на наличие зазора в ферромагнитном магнитопроводе катушки или дросселя (обычно зазор делают для увеличения магнитного сопротивления, чтобы предотвратить насыщение магнитопровода), символ последнего разрывают посередине (см. рис. 4.2, дроссель L4).

Для перестройки колебательных контуров иногда используют катушки переменной индуктивности — так называемые вариометры. Конструктивно вариометр состоит из двух соединенных последовательно и помещенных одна в другую катушек, одна из которых может изменять свое положение по отношению к другой (например, при вращении). Символы катушек, составляющих вариометр, располагают на схемах либо параллельно (рис. 4.3, L1.1, L1.2), либо перпендикулярно друг другу (£2.1, £2.2) и пересекают знаком регулирования. В качестве вариометров применяют также катушки с подвижными магнитопроводами.

Объединение таких катушек в блок показывают штриховой линией механической связи, соединяющей знаки регулирования (см. рис. 4.4, L3.1, L3.2).

Символы катушек используют и в построении условных графических обозначений различных трансформаторов. Простейший трансформатор содержит две индуктивно связанные катушки (обмотки). Эту конструктивную особенность, как и в случае с вариометром, показывают, располагая символы обмоток рядом, параллельно (рис. 4.4) и на схемах им присваивают буквенное обозначение катушек — L. Необходимое для обеспечения работоспособности некоторых устройств фазирование обмоток (т. е. порядок подключения выводов) показывают точками, обозначающими их начало (см. рис. 4.4, L1-L2, L7-L8).

Радиочастотные трансформаторы могут быть как с магнитопроводами, так и без них. Если магнитопровод общий для всех обмоток, его изображают между их символами (см. рис. 4.4, L5-L6, L7-L8), а если каждая из них имеет свой магнитопровод — над ними (L9-L10, L11-L12). Возможность подстройки индуктивности изменением положения сердечника показывают знаком подстроенного регулирования, пересекая им либо только УГО магнитопровода (L9-L10, L11-L12), либо и его, и одновременно символов обмоток (L7-Z8). Если же необходимо показать регулируемую индуктивную связь между обмотками, их символы пересекают знаком регулирования (L3-L4, L11-L12).
Трансформаторы, работающие в широкой полосе частот, обозначают буквой T, а их обмотки римскими цифрами (рис. 4.5). Иногда вместо последних для обозначения обмоток используют условную нумерацию их выводов. Число полуокружностей в символах обмоток трансформаторов может быть любым.

Для уменьшения помех, проникающих из сети, между первичной и вторичными обмотками трансформаторов питания иногда помещают электростатический экран. Он представляет собой незамкнутый виток медной или алюминиевой фольги или один слой тонкого провода, соединяемый с общим проводом устройства. На схемах такой экран изображают штриховой линией (см. рис. 4.5, T1), а соединение с общим проводом — поперечной черточкой на конце вывода экрана. Условное графическое обозначение трансформаторов допускается показывать повернутым на 90°.
Разновидность трансформаторов — автотрансформаторы изображают на схемах, как и катушки с отводами. Возможность плавного регулирования снимаемого с них напряжения показывают знаком регулирования (см. рис. 4.5, T2).

Катушка индуктивности на схеме — Весёлый Карандашик

2013, Апрель 3 , Среда

Самая простая электрическая цепь, состоящая из электрического проводника в виде обычного изолированного провода, и источника переменного тока, представляющего собой понижающий трансформатор, подключённый к бытовой электрической сети, будет примером для описания в этом материале.

В электрической цепи, в которой протекает переменный ток, на величину этого проходящего электрического тока влияет и сопротивление проводника, включённого в цепь, и магнитное поле вокруг проводника, создаваемого при прохождении тока через этот проводник. Получается, что электрическая цепь с переменным током обладает ещё и своими магнитными свойствами, характеризующими величиной, какой является индуктивность. В данном случае — это индуктивность проводника или всей электрической цепи.

Доступными словами будет сказано, чем больше по величине проходящий через проводник переменный ток, тем больше по величине будет создаваемое вокруг этого же проводника переменное магнитное поле.

Но не все проводники обладают одинаковой электрической проводимостью. Каждый материал, используемый для изготовления проводника, обладает своими свойствами, от которых зависит и величина сопротивления электрическому току, называемая активным сопротивлением проводника, и величина индуктивного сопротивления, определяемое индуктивностью проводника, то есть своими магнитными свойствами.

Электрический дроссель.

У прямого проводника сопротивление переменному току, создаваемое магнитным полем проводника, индуктивность небольшая. А если этот же проводник свернуть в катушку, то его индуктивность сразу и на много увеличится. Увеличится его индуктивное сопротивление переменному току и электрический ток в такой цепи уменьшится. Для переменного тока индуктивность полученной катушки является преградой и вокруг катушки образуется электромагнитное поле, величина которого будет зависеть от силы проходящего через катушку переменного тока. А для постоянного тока индуктивность не оказывает такого влияния, как для переменного тока, а определяет своё влияние только лишь активным сопротивлением проводника. Получается, что индуктивная катушка, обладающая большим сопротивлением для переменного тока и очень малым сопротивлением постоянному, будет характеризовать устройство, именуемое электрическим дросселем.

Любой электрический проводник, свёрнутый в катушку, в действующей электрической цепи с переменным током будет представлять собой катушку индуктивности, выполняющую роль дросселя, вариометра(изменяющего индуктивность) или реактора и зависеть от величины и частоты проходящего через катушку тока.

Единицой индуктивности является генри(Гн).

Графическое изображение индуктивных элементов на схеме.

Волнообразная линия, нарисованная параллельно рисунку сердечника или без него и есть наш катушка индуктивности. Напоминает изображение части электрического трансформатора.

Так же как у трансформатора указывается начало обмотки толстой жирной точкой и указывается сердечник, если имеется, а вот обозначается на схеме буквой (L). Рядом устанавливается дополнительный буквенный символ, в зависимости от типа дросселя : L — LL(дроссель ламп люминесцентного освещения), G — LG(реактор), R — LR(обмотка возбуждения генератора).

Катушка индуктивности сама по себе является конструктивной составляющей единицей устройства, а дроссель, вариометр, реактор — это уже целая функционирующая единица устройства, конструкция которого определяется его назначением.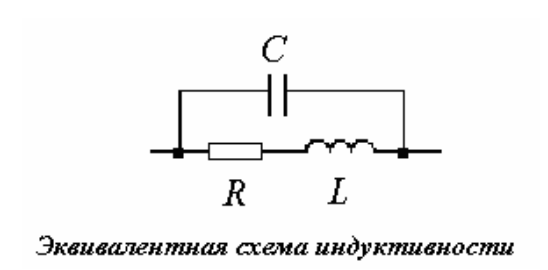 То есть, используемая в электросхеме индуктивная катушка в действующей цепи будет являться или дросселем или реактором или вариометром. В неработающей системе катушка индуктивности будет только катушкой и не больше. Это моё мнение и его никому не навязываю, только лишь делюсь.

«Катушка индуктивности на схеме»

Катушки индуктивности могут иметь винтовую, спиральную или винтоспиральную намотку из изолированного проводника и иметь значительную индуктивность и малое активное сопротивление и малую электрическую ёмкость. Катушки наматываются на каркас с использованием сердечников или без них. Волнообразная линия, нарисованная параллельно рисунку сердечника или без него и есть наш катушка индуктивности. Напоминает изображение части электрического трансформатора.

Игорь Александрович

«Весёлый Карандашик»

Типы катушек индуктивности

Катушкой индуктивности называется пассивный компонент, представляющий собой деталь имеющую обмотку в виде изолированной спирали, которая обладает свойством способным концентрировать переменное магнитное поле. Катушки индуктивности, в отличие от унифицированных резисторов и конденсаторов, являются нестандартными изделиями, а их конфигурация определяется из расчёта на определённое устройство.

Катушки индуктивности обладают характерными параметрами такими как: собственная емкость, добротность, индуктивность и температурная стабильность.

Величина индуктивности катушки прямо пропорциональна габаритным размерам и числу её витков. Индуктивность также зависит от материала сердечника устанавливаемого в катушку и применяемого экрана.

Катушка индуктивности без отводов

Катушка индуктивности с отводами

Вводя в катушку индуктивности стержень, который может быть изготовлен из, феррита, магнетита, железа и т.д. ее индуктивность заметно увеличивается. Подобное свойство позволяет уменьшить общее количество витков катушки и получить требуемую индуктивность. Индуктивность катушки можно регулировать поворотом резьбового сердечника.

В диапазоне коротких волн ( KB ) и ультра коротких волн ( УКВ ) используются катушки с относительно малой индуктивностью. В таких катушках монтируются латунные или алюминиевые сердечники, которые позволяют регулировать индуктивность в пределах плюс минус пяти процентов.

На величину активного сопротивления влияет сопротивление самой обмотки катушки и сопротивлением, из-за потерь электрической энергии в каркасе, сердечнике, экране. Чем меньше величина активного сопротивление, тем выше добротность катушки, а следовательно и ее качество.

Катушка индуктивности магнитодиэлектрическим сердечником

Катушка индуктивности с ферритовым и ферромагнитным сердечником

Индуктивность с диамагнитным сердечником (медь, алюминий, латунь)

Витки катушки, зачастую разделяются слоем изоляции, и тем самым образуют элементарный конденсатор, обладающий некоторой емкостью.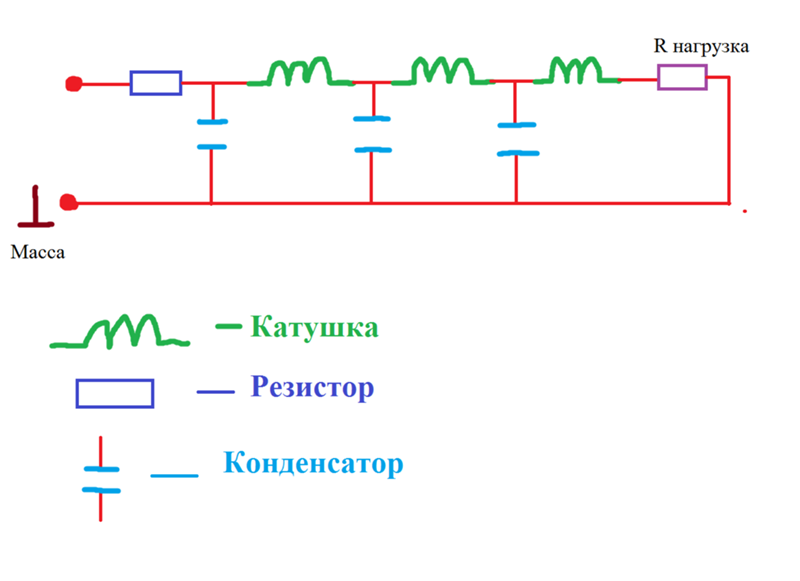 Между отдельными слоями многослойных катушек индуктивности неизбежно образуется ёмкость. Из этого следует, что помимо индуктивности, катушки обладают некоторой емкостной величиной. Наличие собственной емкости катушки является нежелательным фактором, и ее, как правило, стараются уменьшить. Для этих целей используются различные конструкции форм каркасов катушек и специальные технологии намотки провода.

Катушки индуктивности, как правило, наматываются медным проводником, покрытым эмалевой или эмалево-шелковой изоляцией. В случае если требуется намотать катушки для ( ДВ ) длинноволнового и ( СВ ) средневолнового диапазонов используют одножильные проводники типов ПЭЛШО, ПЭЛШД, ПЭЛ, ПЭТ и др. а для ( KB ) коротковолнового и ( УКВ ) ультракоротковолнового диапазонов обычно наматывают проводники одножильного сечения типов ПЭЛ, ПЭЛУ, ПЭТ и др.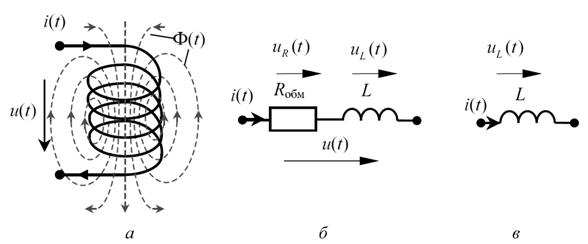

Технология намотки катушек индуктивности может быть различного исполнения. Имеется несколько наиболее распространённых способов укладки провода, это может быть сплошная намотка или с шагом, намотка навалом, а так же типа «универсаль».

Намотка в один слой применяется для изготовления катушек, которые работают в диапазоне коротких и ультракоротких волн. Как правило, индуктивность подобных катушек составляет от нескольких десятков до 500 мкГ. Каркас однослойных катушек имеет цилиндрическую форму и изготовляется из разнообразных материалов с диэлектрическими свойствами.

В случае если требуется получить достаточно большую индуктивность катушки( свыше 500 мкГ), оставляя её минимальные размерные параметры, применяют намотку несколькими слоями. Подобные катушки имеют большую внутреннюю емкость и для ее уменьшения провод укладывают в навал или типа «универсаль».

Катушка с изменяющейся индуктивностью

Катушка с подстройкой

Экранированная индуктивность

Дроссель

Дроссель, это та же катушка индуктивности, которая обладает большим сопротивлением переменному и малым сопротивлением постоянному току. Дроссели используются в качестве электронных компонентов в различных электротехнических и радиотехнических приборах и устройствах.

В радиоэлектронной аппаратуре применяются высокочастотные и низкочастотные дроссели. Дроссели изготовляют с однослойной навивкой, или укладкой проволоки типа «универсаль». Дроссели так же наматываются по секциям, чтобы уменьшить собственную емкость.

Обозначение дросселей на принципиальных схемах производится аналогично катушкам индуктивности и выглядит в виде четырех полуокружностей соединенных между собой.

Индуктивность. Виды катушек и контур. Работа и особенности

Индуктивность характеризует магнитные свойства цепи тока. Она прямо пропорциональна магнитному потоку и обратно пропорциональна силе тока в контуре.

Индуктивность

Электрический ток во время протекания по контуру образует магнитное поле. Индуктивностью называют способность получать энергию от источника тока и создавать из нее магнитное поле.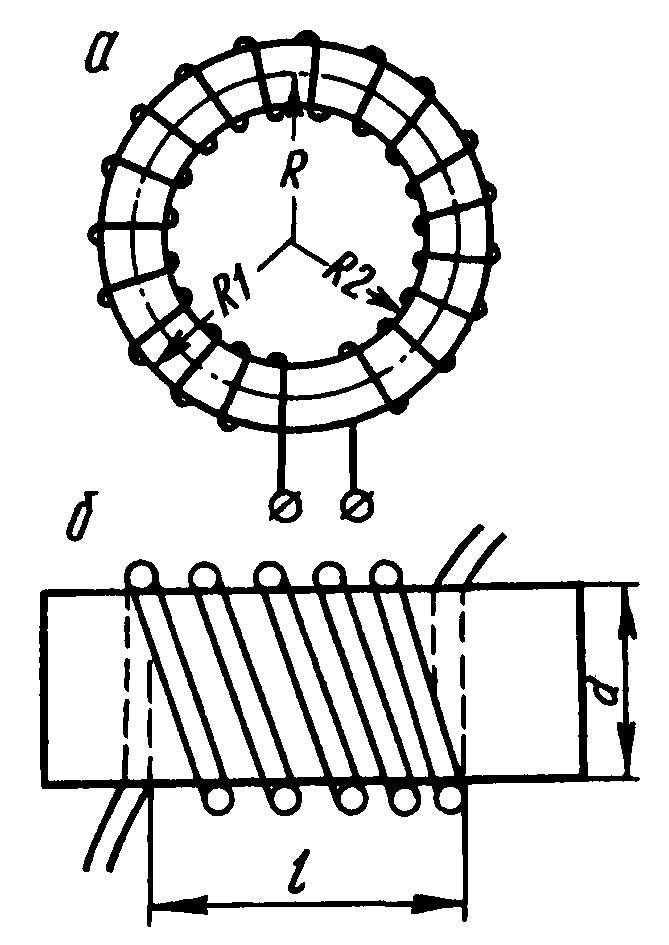

При повышении тока на обмотке магнитное поле повышается, а при снижении уменьшается. Катушкой называется винтовая катушка в виде спирали из изолированного провода, с индуктивностью, при малой емкости и сопротивлении которая имеет единицу измерения Гн (Генри) и определяется по формуле:

L = Φ / I, где L – индуктивность катушки, I – сила тока, Φ – магнитный поток.

Катушка обладает некоторой особенностью. При подаче на нее постоянного напряжения, в ней образуется напряжение, противоположное по знаку, и длящееся очень короткий промежуток времени. Это явление назвали ЭДС самоиндукции. ЭДС – это электродвижущая сила.

При размыкании цепи напряжение и ЭДС суммируются поэтому, сначала ток будет иметь двойную величину, а затем упадет до нуля. Время падения тока зависит от величины индуктивности катушки.

Виды катушек

Катушки можно разделить на типы:

С магнитным сердечником. Его материалом может быть сталь, ферритовый сердечник. Они предназначены для увеличения величины индуктивности.
Без сердечника. Катушки наматываются в виде спирали, на бумажной трубке. Применяются для создания незначительной индуктивности (до 5 мГн).

Чаще всего применяют сердечники из пластин, выполненных из электротехнической стали, для снижения вихревых токов, а также сердечники в виде ферритовых колец различных размеров (тороидальные), обеспечивающие создание значительной индуктивности, в отличие от обычных цилиндрических сердечников.

Катушки со значительной величиной индуктивности выполняют в виде трансформатора с металлическим сердечником. От обычного трансформатора они отличаются числом обмоток. В такой катушке есть одна первичная обмотка, а вторичной нет.

Особенности

При соединении нескольких катушек по параллельной схеме, необходимо следить, чтобы они были расположены на плате друг от друга как можно дальше, во избежание взаимного влияния катушек друг на друга магнитными полями.
Расстояние между витками на тороидальном сердечнике не влияет на свойства индуктивной катушки.
Для создания наибольшей индуктивности витки на катушке необходимо наматывать вплотную между собой.
При использовании в качестве сердечника ферритового цилиндра с наибольшей индуктивностью будет центр.
Чем меньше число витков на катушках, тем ниже у них индуктивности.
При последовательной схеме соединения катушек, общая индуктивность цепи складывается из индуктивностей каждой катушки.

Емкость катушки

Витки обмотки катушки отделены друг от друга диэлектрическим слоем, поэтому они образуют своеобразный конденсатор, который характеризуется своей емкостью. В катушках, имеющих несколько слоев обмотки, емкость образуется между слоями. В результате, катушка имеет свойство не только индуктивности, но и емкости.

Чаще всего емкость катушки оказывает отрицательное воздействие на элементы электрической схемы. Поэтому от емкости катушки избавляются разными способами. Например, каркас катушки изготавливают особой формы, витки наматывают по специальной технологии. При намотке катушки виток к витку, ее емкость также повышается.

Колебательный контур

Если подключить конденсатор и катушку по схеме, изображенной на рисунке, то получается контур колебаний, который широко применяется в радиотехнических устройствах.

Если навести ЭДС в катушке или зарядить конденсатор, то в контуре будут происходить некоторые колебательные процессы. Конденсатор при разряде возбуждает магнитное поле в катушке индуктивности. При истощении заряда конденсатора, катушка возвращает энергию снова в конденсатор, но с противоположным знаком, с помощью ЭДС самоиндукции. Такой процесс повторяется в виде электромагнитных синусоидальных колебаний.

Частота таких колебаний является резонансной частотой, зависящей от индуктивности катушки и емкости конденсатора. Колебательный контур, соединенный по параллельной схеме имеет значительное сопротивление на частоте резонанса.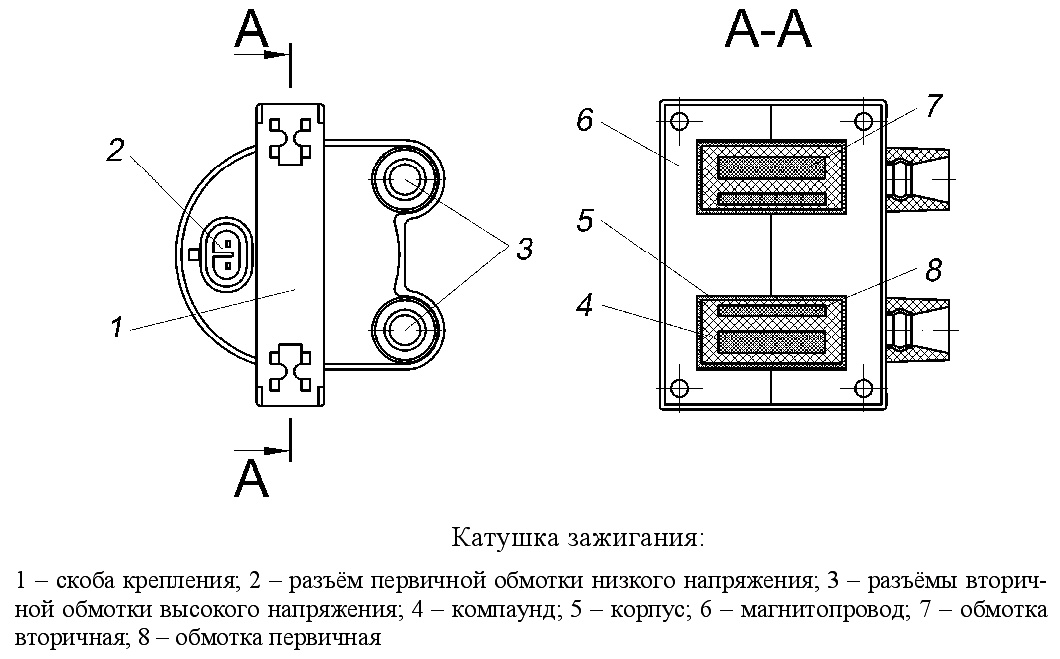 Это дает возможность применять его для избирательности частоты в цепях входа в радиоаппаратуре, а также в усилителях частоты и схемах генераторов частоты.

При параллельной схеме соединения контура колебаний имеются два реактивных элемента, которые обладают разной силой реактивности. Применение такого типа контура позволяет сделать вывод, что при параллельном соединении элементов необходимо суммировать только их проводимости, а не сопротивления. На частоте резонанса сумма проводимостей элементов контура нулевая, что позволяет говорить о сопротивлении переменному току стремящемуся к бесконечности.

За 1 период колебаний действия контура происходит обмен энергией между катушкой и емкостью. В таком случае образуется контурный ток, значительно превосходящий величину тока во внешней цепи.

Индуктивность и конденсатор

Токоведущие части различных устройств могут образовывать индуктивности. Такими частями являются предохранители, токоотводящие шины, соединительные выводы и другие аналогичные части. Если дополнительно присоединить к конденсатору шины, то образуется индуктивность, которая оказывает влияние на работу электрической цепи. Также, на работоспособность цепи влияет емкость и сопротивление.

Индуктивности, образующияся на частоте резонанса вычисляется по формуле:

C_e = C / (1 – 4Π2f2LC), где C_e – это емкость конденсатора (эффективная), f – частота тока, L – индуктивность катушки, С – действительная емкость, П – число «пи».

Величина индуктивности должна всегда учитываться в схемах с силовыми конденсаторами большой емкости. В схемах с импульсными конденсаторами важным фактором является значение собственной индуктивности. Разряд таких конденсаторов происходит на индуктивные контуры, делящиеся на виды:

Колебательные.
Апериодические.

В конденсаторе индуктивность зависит от вида соединения элементов в схеме. При параллельной схеме это значение складывается из индуктивностей элементов схемы. Для снижения индуктивности электрического устройства, необходимо токопроводящие части конденсатора расположить таким образом, чтобы магнитные потоки компенсировались, то есть, проводники с одним направлением тока располагают как можно дальше друг от друга, а с противоположным направлением – рядом друг с другом.

При сближении токоведущих частей и уменьшении диэлектрического слоя можно добиться снижения индуктивности секции конденсатора. Это достигается с помощью разделения одной секции на несколько небольших емкостей.

Катушка индуктивности. Устройство и принцип работы.

Приветствую всех на нашем сайте!

Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.

Устройство и принцип работы катушки индуктивности.

Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку 🙂 То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название 🙂 Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:

А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:

В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек.{-7}\medspace\frac{Гн}{м}

\mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз

S – площадь поперечного сечения катушки

N – количество витков

l – длина катушки

Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.

С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!

Катушка индуктивности в цепи постоянного тока.

Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет 🙂 Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?

Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:

\varepsilon_s = -\frac{d\Phi}{dt}

Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:

На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.

Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).

Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:

После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).

Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:

\varepsilon_s = -L\medspace\frac{dI}{dt}

На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.

Катушка индуктивности в цепи переменного тока.

Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:

Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:

Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:

\varepsilon_L = -L\medspace\frac{dI}{dt}

Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.

Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу 🙂

Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).

А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).

И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:

X_L = w\medspace L

Где w – круговая частота: w = 2 \pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.

Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:

u + \varepsilon_L = 0

А следовательно:

u = – \varepsilon_L

Построим на одном графике зависимости тока и напряжения в цепи от времени:

Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:

При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.

Вот и с включением катушки в цепь переменного тока мы разобрались!

На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!

Закон индукции Фарадея: Закон Ленца

Цели обучения

К концу этого раздела вы сможете:

Рассчитайте ЭДС, ток и магнитные поля, используя закон Фарадея.
Объясните физические результаты Закона Ленца

Закон Фарадея и Ленца

Эксперименты Фарадея показали, что ЭДС, вызванная изменением магнитного потока, зависит только от нескольких факторов. Во-первых, ЭДС прямо пропорциональна изменению магнитного потока Δ Φ .Во-вторых, ЭДС является наибольшей, когда изменение во времени Δ t наименьшее, то есть ЭДС обратно пропорциональна Δ t . Наконец, если катушка имеет Н витков, будет создана ЭДС, которая в Н, раз больше, чем для одиночной катушки, так что ЭДС прямо пропорциональна Н . Уравнение для ЭДС, вызванной изменением магнитного потока, равно

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].

Это соотношение известно как закон индукции Фарадея .Обычно единицами измерения ЭДС являются вольты. Знак минус в законе индукции Фарадея очень важен. Минус означает, что ЭДС создает ток I и магнитное поле B, которые препятствуют изменению потока Δ Φ — это известно как закон Ленца . Направление (обозначенное знаком минус) ЭДС настолько важно, что оно было названо законом Ленца в честь русского Генриха Ленца (1804–1865), который, подобно Фарадею и Генри, независимо исследовал аспекты индукции. Фарадей знал о направлении, но Ленц так ясно изложил его, что ему приписывают его открытие.(См. Рисунок 1.)

Рис. 1. (a) Когда стержневой магнит вставляется в катушку, сила магнитного поля в катушке увеличивается. Ток, наведенный в катушке, создает другое поле в направлении, противоположном направлению стержневого магнита, чтобы противодействовать увеличению. Это один из аспектов закона Ленца: индукция препятствует любому изменению потока. (b) и (c) — две другие ситуации. Убедитесь сами, что показанное направление индуцированной катушки B действительно противодействует изменению магнитного потока и что показанное направление тока согласуется с RHR-2.

Стратегия решения проблем закона Ленца

Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:

Сделайте набросок ситуации для использования при визуализации и записи направлений.
Определите направление магнитного поля B.
Определите, увеличивается или уменьшается поток.
Теперь определите направление индуцированного магнитного поля B. Оно противостоит изменению магнитного потока путем добавления или вычитания из исходного поля.
Используйте RHR-2 для определения направления индуцированного тока I, ответственного за индуцированное магнитное поле B.
Направление (или полярность) наведенной ЭДС теперь будет управлять током в этом направлении и может быть представлено как ток, выходящий из положительного вывода ЭДС и возвращающийся к его отрицательному выводу.

Для практики примените эти шаги к ситуациям, показанным на Рисунке 1, и другим, которые являются частью следующего текстового материала.

Применение электромагнитной индукции

Существует множество применений закона индукции Фарадея, которые мы исследуем в этой и других главах. На этом этапе позвольте нам упомянуть несколько, которые связаны с хранением данных и магнитными полями. Очень важное приложение связано с аудио и видео , записывающими лентами . Пластиковая лента, покрытая оксидом железа, проходит мимо записывающей головки. Эта записывающая головка представляет собой круглое железное кольцо, вокруг которого намотана катушка с проволокой — электромагнит (рис. 2).Сигнал в виде переменного входного тока от микрофона или камеры поступает на записывающую головку. Эти сигналы (которые являются функцией амплитуды и частоты сигнала) создают переменные магнитные поля на записывающей головке. Когда лента движется мимо записывающей головки, ориентация магнитного поля молекул оксида железа на ленте изменяется, таким образом записывая сигнал. В режиме воспроизведения намагниченная лента проходит мимо другой головки, аналогичной по конструкции записывающей головке. Различная ориентация магнитного поля молекул оксида железа на ленте индуцирует ЭДС в проволочной катушке в воспроизводящей головке.Затем этот сигнал отправляется на громкоговоритель или видеоплеер.

Рис. 2. Головки для записи и воспроизведения, используемые с аудио- и видеомагнитными лентами. (кредит: Стив Юрветсон)

Аналогичные принципы применимы и к жестким дискам компьютера, только с гораздо большей скоростью. Здесь записи находятся на вращающемся диске с покрытием. Исторически считывающие головки создавались по принципу индукции. Однако входная информация передается в цифровой, а не аналоговой форме — на вращающемся жестком диске записывается серия нулей или единиц.Сегодня большинство считывающих устройств с жестких дисков не работают по принципу индукции, а используют технологию, известную как гигантское магнитосопротивление . (Открытие того факта, что слабые изменения магнитного поля в тонкой пленке из железа и хрома могут вызывать гораздо большие изменения электрического сопротивления, было одним из первых крупных успехов нанотехнологии.) Еще одно применение индукции можно найти на магнитной полосе на магнитной полосе. на оборотной стороне вашей личной кредитной карты, которая использовалась в продуктовом магазине или в банкомате.Это работает по тому же принципу, что и аудио- или видеопленка, упомянутая в последнем абзаце, в которой голова считывает личную информацию с вашей карты.

Еще одно применение электромагнитной индукции — это когда электрические сигналы должны передаваться через барьер. Рассмотрим кохлеарный имплант , показанный ниже. Звук улавливается микрофоном на внешней стороне черепа и используется для создания переменного магнитного поля. Ток индуцируется в приемнике, закрепленном в кости под кожей, и передается на электроды во внутреннем ухе.Электромагнитная индукция может использоваться и в других случаях, когда электрические сигналы должны передаваться через различные среды.

Рисунок 3. Электромагнитная индукция, используемая при передаче электрического тока через среды. Устройство на голове ребенка индуцирует электрический ток в приемнике, закрепленном в кости под кожей. (кредит: Бьорн Кнетч)

Еще одна современная область исследований, в которой электромагнитная индукция успешно реализуется (и имеет значительный потенциал), — это транскраниальное магнитное моделирование.Множество расстройств, включая депрессию и галлюцинации, можно объяснить нерегулярной локальной электрической активностью в головном мозге. В транскраниальной магнитной стимуляции быстро меняющееся и очень локализованное магнитное поле помещается рядом с определенными участками, идентифицированными в головном мозге. В идентифицированных участках индуцируются слабые электрические токи, которые могут привести к восстановлению электрических функций в тканях мозга.

Апноэ сна («остановка дыхания») поражает как взрослых, так и младенцев (особенно недоношенных детей, и это может быть причиной внезапной детской смерти [SID]).У таких людей дыхание может неоднократно останавливаться во время сна. Прекращение действия более чем на 20 секунд может быть очень опасным. Инсульт, сердечная недостаточность и усталость — вот лишь некоторые из возможных последствий для человека, страдающего апноэ во сне. У младенцев проблема заключается в задержке дыхания на это более длительное время. В одном из типов мониторов, предупреждающих родителей о том, что ребенок не дышит, используется электромагнитная индукция. В проводе, обмотанном вокруг груди младенца, проходит переменный ток. Расширение и сжатие грудной клетки младенца во время дыхания изменяет площадь спирали.В расположенной рядом катушке датчика индуцируется переменный ток из-за изменения магнитного поля исходного провода. Если ребенок перестанет дышать, наведенный ток изменится, и родители могут быть предупреждены.

Подключение: сохранение энергии

Закон Ленца является проявлением сохранения энергии. Индуцированная ЭДС создает ток, который противодействует изменению потока, потому что изменение потока означает изменение энергии.Энергия может входить или уходить, но не мгновенно. Закон Ленца — следствие. Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение. Фактически, если бы индуцированная ЭДС была в том же направлении, что и изменение потока, была бы положительная обратная связь, которая не давала бы нам бесплатную энергию из любого видимого источника — закон сохранения энергии был бы нарушен.

Пример 1. Расчет ЭДС: насколько велика наведенная ЭДС?

Рассчитайте величину наведенной ЭДС, когда магнит, показанный на Рисунке 1 (а), вдавливается в катушку, учитывая следующую информацию: одноконтурная катушка имеет радиус 6.00 см, а среднее значение B cos θ (это дано, поскольку поле стержневого магнита сложное) увеличивается с 0,0500 Тл до 0,250 Тл за 0,100 с.

Стратегия

Чтобы найти величину ЭДС , мы используем закон индукции Фарадея, как указано в [latex] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex], но без знака минус, указывающего направление:

[латекс] \ text {emf} = N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].

Раствор

Нам дано, что N = 1 и Δ t = 0.100 с, но мы должны определить изменение потока Δ Φ , прежде чем мы сможем найти ЭДС. Поскольку площадь петли фиксирована, мы видим, что

ΔΦ = Δ ( BA cos θ ) = AΔ ( B cos θ ).

Теперь Δ ( B cos θ ) = 0,200 Тл, поскольку было задано, что B cos θ изменяется от 0,0500 до 0,250 Тл. Площадь контура A = πr2 = (3,14…) ( 0,060 м) ² = 1,13 × 10 ⁻² м ².{2} \ right) \ left (0.200 \ text {T} \ right)} {0.100 \ text {s}} = 22.6 \ text {mV} \\ [/ latex].

Обсуждение

Хотя это напряжение легко измерить, его явно недостаточно для большинства практических приложений. Больше петель в катушке, более сильный магнит и более быстрое движение делают индукцию практическим источником напряжения, которым она и является.

Исследования PhET: Электромагнитная лаборатория Фарадея

Поиграйте с стержневым магнитом и катушками, чтобы узнать о законе Фарадея.Поднесите стержневой магнит к одной или двум катушкам, чтобы лампочка загорелась. Просмотрите силовые линии магнитного поля. Измеритель показывает направление и величину тока. Просмотрите силовые линии магнитного поля или используйте измеритель, чтобы показать направление и величину тока. Вы также можете играть с электромагнитами, генераторами и трансформаторами!

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

Концептуальные вопросы

Человек, работающий с большими магнитами, иногда помещает голову в сильное поле.Она сообщает, что у нее кружится голова, когда она быстро поворачивает голову. Как это может быть связано с индукцией?
Ускоритель частиц отправляет заряженные частицы с высокой скоростью по откачанной трубе. Объясните, как катушка с проволокой, намотанная вокруг трубы, может обнаруживать прохождение отдельных частиц. Нарисуйте график выходного напряжения катушки при прохождении через нее одиночной частицы.

Задачи и упражнения

1. Как показано на Рисунке 5 (а), каково направление тока, индуцируемого в катушке 2: (а) Если ток в катушке 1 увеличивается? (b) Если ток в катушке 1 уменьшается? (c) Если ток в катушке 1 постоянный? Ясно покажите, как вы следуете шагам из приведенной выше стратегии решения проблем для закона Ленца .

Рис. 5. (a) Катушки лежат в одной плоскости. (б) Проволока находится в плоскости катушки.

2. Как показано на Рисунке 5 (b), каково направление тока, индуцируемого в катушке: (a) Если ток в проводе увеличивается? (б) Если ток в проводе уменьшится? (c) Если ток в проводе внезапно меняет направление? Ясно покажите, как вы следуете шагам из приведенной выше стратегии решения проблем для закона Ленца .

3. Как показано на Рисунке 6, каковы направления токов в катушках 1, 2 и 3 (предположим, что катушки лежат в плоскости цепи): (a) Когда переключатель в первый раз замыкается? (б) Когда выключатель был замкнут в течение длительного времени? (c) Сразу после размыкания переключателя?

Рисунок 6.

4. Повторите предыдущую проблему с перевернутой батареей.

5. Убедитесь, что единицами измерения Δ Φ / Δ т являются вольты. То есть показать, что 1 Тл м ² / с = 1 В.

6. Предположим, что 50-витковая катушка лежит в плоскости страницы в однородном магнитном поле, направленном внутрь страницы. Змеевик изначально имел площадь 0,250 м ². Он растягивается, чтобы не было площади за 0,100 с. Каковы направление и величина наведенной ЭДС, если однородное магнитное поле имеет напряженность 1.50 т?

7. (a) Техник МРТ перемещает свою руку из области очень низкой напряженности магнитного поля в поле 2,00 Тл сканера МРТ, указывая пальцами в направлении поля. Найдите среднюю ЭДС, индуцированную в его обручальном кольце, учитывая его диаметр 2,20 см и предполагая, что для его перемещения в поле требуется 0,250 с. (б) Обсудите, может ли этот ток существенно изменить температуру кольца.

8. Integrated Concepts Обратимся к ситуации в предыдущей задаче: (a) Какой ток индуцируется в кольце, если его сопротивление равно 0.0100 Ом? (б) Какая средняя мощность рассеивается? (c) Какое магнитное поле индуцируется в центре кольца? (d) Каково направление индуцированного магнитного поля относительно поля МРТ?

9. ЭДС индуцируется вращением катушки с 1000 витками диаметром 20,0 см в магнитном поле Земли 5,00 × 10 ⁻⁵ Тл. Какая средняя ЭДС индуцируется, если плоскость катушки изначально перпендикулярна полю Земли и повернута параллельно полю за 10,0 мс?

10.Катушка с 500 витками радиусом 0,250 м поворачивается на одну четверть оборота за 4,17 мс, первоначально ее плоскость перпендикулярна однородному магнитному полю. (Это 60 об / с.) Найдите напряженность магнитного поля, необходимую для индукции средней ЭДС 10 000 В.

11. Integrated Concepts Примерно как ЭДС, наведенная в петле на рисунке 5 (b), зависит от расстояния центра петли от провода?

12. Integrated Concepts (a) Молния создает быстро меняющееся магнитное поле.Если болт ударяется о землю вертикально и действует как ток в длинном прямом проводе, он вызывает напряжение в петле, выровненной, как показано на рисунке 5 (b). Какое напряжение индуцируется в петле диаметром 50,0 м 1,00 м от удара молнии 2,00 × 10 6 , если ток падает до нуля за 25,0 мкс? (b) Обсудите обстоятельства, при которых такое напряжение может привести к заметным последствиям.

Глоссарий

Закон индукции Фарадея:: средство вычисления ЭДС в катушке из-за изменения магнитного потока, заданное как [latex] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex]

Закон Ленца:: знак минус в законе Фарадея, означающий, что ЭДС, индуцированная в катушке, противодействует изменению магнитного потока.

Избранные решения проблем и упражнения

1.(a) CCW (b) CW (c) Отсутствие индуцированного тока

3. (a) 1 против часовой стрелки, 2 против часовой стрелки, 3 по часовой стрелке (b) 1, 2 и 3 без тока индуцированного (c) 1 CW, 2 CW, 3 CCW

7. (a) 3,04 мВ (b) В качестве нижнего предела для кольца, оценка R = 1,00 мОм. Передаваемое тепло составит 2,31 мДж. Это небольшое количество тепла.

9. 0,157 В

11. пропорционально [латексу] \ frac {1} {r} \\ [/ latex]

Закон Ленца — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

Используйте закон Ленца для определения направления наведенной ЭДС при изменении магнитного потока
Используйте закон Фарадея с законом Ленца для определения наведенной ЭДС в катушке и соленоиде.

Направление, в котором индуцированная ЭДС движет ток по проволочной петле, можно определить через отрицательный знак.Однако обычно это направление легче определить с помощью закона Ленца, названного в честь его первооткрывателя Генриха Ленца (1804–1865). (Фарадей также открыл этот закон, независимо от Ленца.) Мы формулируем закон Ленца следующим образом:

Закон Ленца

Направление индуцированной ЭДС движет ток по проволочной петле, чтобы всегда противодействовать изменению магнитного потока, вызывающему ЭДС.

Закон Ленца также можно рассматривать с точки зрения сохранения энергии. Если толкание магнита в катушку вызывает ток, энергия в этом токе должна исходить откуда-то.Если индуцированный ток вызывает магнитное поле, противодействующее увеличению поля магнита, который мы втолкнули, тогда ситуация ясна. Мы приложили магнит к полю и поработали с системой, и это проявилось как ток. Если бы индуцированное поле не препятствовало изменению магнитного потока, магнит был бы втянут, создавая ток без каких-либо действий. Была бы создана электрическая потенциальная энергия, нарушив закон сохранения энергии.

Чтобы определить наведенную ЭДС, вы сначала рассчитываете магнитный поток, а затем получаете Величину, заданную по формуле. Наконец, вы можете применить закон Ленца для определения значения.Это будет развиваться на примерах, которые иллюстрируют следующую стратегию решения проблем.

Стратегия решения проблем: закон Ленца

Чтобы использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС:

Сделайте набросок ситуации для использования при визуализации и записи направлений.
Определить направление приложенного магнитного поля
Определите, увеличивается или уменьшается его магнитный поток.
Теперь определите направление индуцированного магнитного поля. Индуцированное магнитное поле пытается усилить магнитный поток, который уменьшается, или противодействует магнитному потоку, который увеличивается. Следовательно, индуцированное магнитное поле добавляет или вычитает приложенное магнитное поле, в зависимости от изменения магнитного потока.
Используйте правило правой руки 2 (RHR-2; см. Магнитные силы и поля), чтобы определить направление индуцированного тока I , ответственного за индуцированное магнитное поле
Направление (или полярность) наведенной ЭДС теперь может управлять обычным током в этом направлении.

Давайте применим закон Ленца к системе (Рисунок) (a). Мы обозначаем «перед» замкнутой проводящей петли как область, содержащую приближающийся стержневой магнит, а «заднюю часть» петли как другую область. По мере того, как северный полюс магнита движется к петле, поток через петлю из-за поля магнита увеличивается, потому что напряженность силовых линий, направленных от передней части петли к задней, увеличивается. Поэтому в контуре индуцируется ток. По закону Ленца направление индуцированного тока должно быть таким, чтобы его собственное магнитное поле было направлено таким образом, чтобы противостояло изменяющемуся потоку, вызванному полем приближающегося магнита.Следовательно, индуцированный ток циркулирует так, что силовые линии его магнитного поля через петлю направлены от задней части петли к передней. При использовании RHR-2 поместите большой палец напротив силовых линий магнитного поля, то есть к стержневому магниту. Ваши пальцы сгибаются против часовой стрелки, если смотреть со стороны стержневого магнита. В качестве альтернативы мы можем определить направление индуцированного тока, рассматривая токовую петлю как электромагнит, который противодействует приближению северного полюса стержневого магнита.Это происходит, когда индуцированный ток течет, как показано, поскольку тогда поверхность петли ближе к приближающемуся магниту также является северным полюсом.

Изменение магнитного потока, вызванное приближением магнита, индуцирует ток в контуре. (а) Приближающийся северный полюс индуцирует ток против часовой стрелки по отношению к стержневому магниту. (b) Приближающийся южный полюс индуцирует ток по часовой стрелке относительно стержневого магнита.

На части (b) рисунка показан южный полюс магнита, движущийся к проводящей петле.В этом случае поток через петлю из-за поля магнита увеличивается, потому что количество силовых линий, направленных от задней части петли к передней, увеличивается. Чтобы противодействовать этому изменению, в петле индуцируется ток, силовые линии которого через петлю направлены спереди назад. Точно так же можно сказать, что ток течет в таком направлении, что поверхность петли, расположенная ближе к приближающемуся магниту, является южным полюсом, который затем отталкивает приближающийся южный полюс магнита.При использовании RHR-2 ваш большой палец направлен в сторону от стержневого магнита. Ваши пальцы сгибаются по часовой стрелке, что соответствует направлению индуцированного тока.

Другой пример, иллюстрирующий использование закона Ленца, показан на (Рисунок). Когда переключатель разомкнут, уменьшение тока через соленоид вызывает уменьшение магнитного потока через его катушки, что вызывает ЭДС в соленоиде. Эта ЭДС должна противодействовать вызывающему его изменению (прекращению тока). Следовательно, наведенная ЭДС имеет указанную полярность и движется в направлении исходного тока.Это может вызвать дугу на выводах переключателя при его размыкании.

(а) Соленоид, подключенный к источнику ЭДС. (b) Размыкающий переключатель S прекращает подачу тока, что, в свою очередь, вызывает в соленоиде ЭДС. (c) Разность потенциалов между концами заостренных стержней создается за счет индукции ЭДС в катушке. Эта разность потенциалов достаточно велика, чтобы образовалась дуга между острыми точками.

Проверьте свое понимание Найдите направление индуцированного тока в проводной петле, показанной ниже, когда магнит входит, проходит и покидает петлю.

Для показанного наблюдателя ток течет по часовой стрелке по мере приближения магнита, уменьшается до нуля, когда магнит центрируется в плоскости катушки, а затем течет против часовой стрелки, когда магнит покидает катушку.

Проверьте свое понимание Проверьте направления наведенных токов на (рисунок).

Сводка

Мы можем использовать закон Ленца для определения направлений индуцированных магнитных полей, токов и ЭДС.
Направление наведенной ЭДС всегда противодействует изменению магнитного потока, вызывающему ЭДС, результат, известный как закон Ленца.

Концептуальные вопросы

Круглые токопроводящие петли, показанные на прилагаемом рисунке, параллельны, перпендикулярны плоскости страницы и соосны. (a) Когда переключатель S замкнут, в каком направлении индуцируется ток в D ? (b) Когда переключатель разомкнут, какое направление тока индуцируется в контуре D ?

а.CW со стороны схемы; б. Против часовой стрелки, если смотреть со стороны схемы

Северный полюс магнита перемещается к медной петле, как показано ниже. Если вы смотрите на петлю сверху магнита, скажете ли вы, что индуцированный ток циркулирует по или против часовой стрелки?

На прилагаемом рисунке показано проводящее кольцо в различных положениях при его движении в магнитном поле. В чем смысл индуцированной ЭДС для каждой из этих позиций?

При входе в петлю наведенная ЭДС создает ток против часовой стрелки, а при выходе из петли индуцированная ЭДС создает непрерывный ток.В то время как петля полностью находится внутри магнитного поля, нет изменения потока и, следовательно, нет индуцированного тока.

Покажите, что и у вас такие же единицы.

Укажите направление индуцированного тока для каждого случая, показанного ниже, наблюдая со стороны магнита.

а. Против часовой стрелки, если смотреть со стороны магнита; б. CW, если смотреть со стороны магнита; c. CW, если смотреть со стороны магнита; d. Против часовой стрелки, если смотреть со стороны магнита; е. CW, если смотреть со стороны магнита; f. нет тока

Проблемы

Одновитковая круговая петля из проволоки радиусом 50 мм расположена в плоскости, перпендикулярной пространственно однородному магнитному полю.За интервал времени 0,10 с величина поля равномерно увеличивается от 200 до 300 мТл. (а) Определите ЭДС, наведенную в петле. (б) Если магнитное поле направлено за пределы страницы, каково направление тока, индуцируемого в петле?

а. ; б. CCW с той же точки зрения, что и магнитное поле

При первом включении магнитного поля поток через 20-витковую петлю изменяется со временем в зависимости от того, где он находится в милливеберах, t — в секундах, а петля находится в плоскости страницы с нормальным направлением единицы. наружу.(а) Какая ЭДС индуцируется в контуре как функция времени? Каково направление индуцированного тока при (b) t = 0, (c) 0,10, (d) 1,0 и (e) 2,0 с?

а. 150 А вниз через резистор; б. 46 А вверх через резистор; c. 0,019 А вниз через резистор

Используйте закон Ленца для определения направления индуцированного тока в каждом случае.

Глоссарий

Закон Ленца: направление наведенной ЭДС противодействует изменению магнитного потока, который ее произвел; это отрицательный знак в законе Фарадея

Общая физика II

Глава 31

Вопросы 2, 5, 7, 9, 12, 14, 15

Проблемы: 1, 3, 6, 7, 17, 20

Q2 Петля из проволоки помещена в однородный магнитный поле.При какой ориентации витка магнитный поток максимален? Для какой ориентации поток равен нулю?

Магнитный поток максимален, когда магнитное поле B перпендикулярно петле провода, как на схеме здесь:

Магнитный поток минимален — фактически равен нулю — когда магнитное поле B параллельно проволочной петле, как на схеме здесь:

Для наглядности показалось, что лучше нарисовать это почти параллельно, а не точно параллельно.

Q5 Полоса на рис. 31.24 перемещается по рельсам к вправо со скоростью v и однородным постоянным магнитным полем направлен за пределы страницы. Почему индуцированный ток по часовой стрелке ? Если бы штанга двигалась влево, в каком бы направлении индуцированный ток?

Существует магнитная сила из-за движения через магнитное поле. поле.

F _mag = q v х В

дает вектор вниз для положительного заряда (и вектор вверх для отрицательного заряда).Ток в направлении движение положительного заряда.

, значит, ток течет по движущейся полосе, влево по нижнему проводнику, вверх через резистор, и до справа по верхнему проводнику. Это по часовой стрелке протекать по всему контуру.

При изменении направления скорости

что меняет все.Теперь вектор v x B указывает вверх. Это направление магнитной силы на положительном заряжать.

, так что ток течет вверх по движущемуся проводнику. Чтобы замкнуть цепь, ток должен течь слева вверху. провод, через резистор вниз и вправо в нижнем проводе. Это означает поворот против часовой стрелки. ток по всей цепи.

Q7 Большая круглая петля из проволоки лежит в горизонтальной плоскости. самолет. Через петлю пропускают стержневой магнит. Если ось магнита остается горизонтальным при падении, опишите наведенную в петле ЭДС. Как изменяется установка, если ось магнита остается вертикальной как падает?

Когда стержень магнит падает горизонтально — ну падает вертикально, но лежит в горизонтальном положении — во всяком случае, когда он падает, как показано здесь, поток через горизонтальную катушку будет небольшим.Поток мал, потому что магнитное поле почти параллельно магнитному полю. катушка и направление магнитного поля таковы, что если учесть компонентов, перпендикулярных катушке, примерно столько же положительных поток как отрицательный поток. Таким образом, если поток небольшой, изменение потока будет также быть маленьким.

Однако, когда магнит падает, как показано здесь, с его ось вертикальна, поток через катушку намного больше — поэтому изменение потока также будет больше.

Q9 Будет уронить магнит на длинную медную трубку произвести ток в трубке?

Да, это интересная и полезная демонстрация.

Q12 Что происходит, когда скорость, с которой катушка генератора вращается увеличивается?

Увеличение скорости увеличивает скорость, с которой поток изменяется так, что увеличивает ЭДС или напряжение!

Q14 Когда переключатель на Рисунке 31.25а закрыта, а ток устанавливается в катушке, а металлическая кольцевая пружина направлена вверх, как показано на рисунке. 31.25b. Почему?

Изменяющийся ток в катушке вызывает изменение магнитного поле в железном сердечнике. Это изменяющееся магнитное поле вызывает индуцированное напряжение и ток в металлическом кольце. По закону Ленца это индуцированное напряжение или ток создаст магнитное поле в направлении, противоположном магнитное поле в железном сердечнике.Эти два поля отталкивают друг друга!

Q15 Предположим, батарея, показанная на рисунке 31.25a, заменена. источником переменного тока, и переключатель удерживается замкнутым. Если удерживать, металл кольцо в верхней части соленоида нагревается. Почему ?

В приведенном выше объяснении просто сказано «изменение тока». и «изменяющееся магнитное поле». Они могут измениться, потому что они переходят от нуля к некоторому значению или могут меняться, потому что они являются частью цепи переменного тока.Результат точно тоже самое.

Если продолжать удерживать кольцо в чередующемся (меняющемся) магнитное поле, в нем по-прежнему будет ток. Токи производят нагревать!

31,1 Прямоугольная катушка на 50 витков размером 5,0 см x 10,0 см опускается из положения, где B = 0, в новое положение, в котором B = 0,50 Тл и направлено перпендикулярно плоскости катушки.Рассчитать результирующая средняя ЭДС, индуцированная в катушке, если происходит смещение через 0,25 с.

= — N d / dt = — Н / т

= _f — _и

_и = 0

_f = [0,5 т] [(0,05 м) (0,10 м)] = 0,0025 т-м ²

= _f — _и = 0.0025 Т-м ²

= — N d / dt = — Н / т = — (50) (0,0025 / 0,25) В

= — 0,50 В

31,3 Мощный электромагнит имеет поле 1,6 Тл и поперечное сечение площадь 0,20 м ². Если разместить катушку на 200 витков и общее сопротивление 20 Ом вокруг электромагнита, а затем включите отключение питания электромагнита за 20 мс (0.020 с), какой ток наводится в катушке?

= — N d / dt = — Н / т

= _f — _и

_f = 0

_и = [1,6 т] [0,20 м ²] = 0,32 т / м ²

= _f — _и = — 0,32 Т-м ²

= — N d / dt = — Н / т = (200) (0.32 / 0,020) В

= 3200 В

31,6 Плотно намотанная круглая катушка имеет 50 витков радиуса каждого 0,10 м. Однородное магнитное поле включается в направлении, перпендикулярном к плоскости катушек. Если поле линейно возрастает от 0 T до 0,6 Тл за 0,20 с, какая ЭДС индуцируется в катушке?

А = р ²

А = (0.10 м) ² = 0,0314 м ²

= A B

cos = cos 0 = 1

_и = 0

_f = (0,0314 м ²) (0,6 Тл) = 0,01885 Тлн ²

= _f — _и = — 0,01885 Т-м ²

= — N d / dt = — Н / т = (50) (0.01885 / 0,020) В

= 47 В

31,7 30-витковая круглая катушка радиусом 4 см и сопротивлением 1 Ом помещается в магнитное поле, направленное перпендикулярно плоскости катушки. Величина магнитного поля меняется во времени в зависимости от к выражению B = 0,010 t + 0,040 t ², где t в секундах а B находится в тесле. Рассчитать наведенную ЭДС в катушке при t = 5,0 с.

B = 0,010 т + 0,040 т ²

дБ / dt = 0,010 + (0,040) (2 т)

При t = 5,0 с

дБ / dt] _{(5,0 с)} = 0,010 + (0,040) (2 x 5)

дБ / dt] _{(5,0 с)} = 0,010 + (0,040) (10)

дБ / dt] _{(5,0 с)} = 0,010 + 0,40 = 0,41

А = р ²

А = (0,04 м) ² = 0.005 м ²

= A B

, поскольку cos = cos 0 = 1

= — N d / dt = — N d (AB) / dt = — NA дБ / dt

= — (30) (0,005) (0,41) V = 0,062 В

Хотя это все, что требует учебник, поскольку мы также знать сопротивление катушки, мы могли бы также увеличить это просто бит и запросить ток , индуцированный в катушке.

В = ИК

I = V / R

I = 0,062 В / 1

I = 0,062 А

31,17 Летит самолет Boeing 747 с размахом крыла 60,0 м. по горизонтали со скоростью 300 м / с над Фениксом, где направление Магнитного поля Земли составляет 58 ^o ниже горизонтали. Если намагниченность магнитного поля 50,0 Тл (microTeslas), какое напряжение возникает между законцовками крыла?

Самолет Boeing 747 с размахом крыла 60.0 м летит по горизонтали со скоростью 300 м / с над Фениксом, где направление Магнитного поля Земли составляет 58 ^o ниже горизонтали. Если величина магнитного поля 50,0 Тл (microTeslas), какое напряжение возникает между законцовками крыла?

Для случая v перпендикулярно B , мы найдено

= — B l v

Но это компонент B , который перпендикулярен на v (или наоборот!), что важно, поэтому более общий форма этого уравнения действительно

= — B l v sin

где угол между B и v

= — B l v sin

= — B l v sin 58 ^o

= — (50 x 10 ^{— 6}) (60) (300) (0.790) В

= — 0,711 В

31.20 На рисунке P31.20 стержневой магнит перемещен к петле. Является ли V _a — V _b положительным, отрицательным или нулевым?

С чем нам работать? Закон Ленца говорит нам, что индуцированный ток будет пытаться вернуть поток к тому, что он было до изменения («status quo ante»).

Изначально, когда магнит находится далеко, поток через петля нулевая.

По мере того, как магнит перемещается в катушку, магнитный поток увеличивается. В каком направлении находится магнитное поле?

Магнитное поле направлено от ортогонального полюса N к выносной столб S . На этом этапе может быть немного проще перерисовать магнитное поле как единый вектор.

Теперь мы изменили без потока на имеющий поток из-за магнитного поля, указывающего на экран « назад ».Согласно закону Ленца индуцированное магнитное поле будет противодействовать это изменение.

«Индуцированное магнитное поле» равно магнитному полю. поле, вызванное индуцированным током .

Следовательно, индуцированный ток в контуре должен будет по часовой стрелке , когда мы смотрим на это. Это означает, что ток в остальная часть схемы должна быть такой, как показано стрелками на рисунке выше.

Все это означает, что через резистор протекает ток. R от a до b . Для этого необходимо, чтобы напряжение на a было выше. чем напряжение на b.

V _a> V _b

Электромагнетизм

— стержневой магнит, пропущенный через катушку

Пояснение для неспециалистов:

Давным-давно магнит был далеко, и магнитный поток через катушку был практически нулевым.

Если вы измеряете наведенную ЭДС как функцию времени по оси x и индуцированную ЭДС в качестве оси Y, тогда площадь под кривой над осью x между вертикальными линиями $ t = t_1 $ и вертикальной линия $ t = t_2 $ — полное изменение магнитного потока от времени $ t_1 $ до момента $ t_2 $.Это закон физики, известный как закон Фарадея. Это не объясняется чем-то более фундаментальным и мотивируется своим согласием с экспериментальными наблюдениями.

Примените это к предыдущему абзацу, и область под графиком ЭДС до некоторой линии $ t = T $ будет фактическим магнитным потоком, проходящим через катушку в момент времени $ t = T $.

По мере того, как стержневой магнит падает, поток становится все больше и больше, пока магнит не окажется буквально внутри петли. Вы можете убедиться в этом, нарисовав силовые линии магнитного поля вокруг магнита и представив себе различные места, где могла бы быть петля.Если все силовые линии центрированы на петле, они проходят через середину магнита и выходят из северного полюса, и каждая из них проходит по большой петле, прежде чем развернуться и вернуться обратно через южный полюс магнита. У каждого есть некоторое расстояние, где он полностью указывает в противоположном направлении, как когда он идет с севера на юг. Те, которые вращаются вне катушки, вносят свой вклад в магнитный поток, потому что тот, что идет на север, вносит свой вклад, и та же силовая линия находилась за пределами катушки, когда она указывала на юг.Те, которые вращаются внутри петли, входят и выходят, и сеть не вносит никакого потока (они вносят равное количество положительного и отрицательного потока). Если вы выберете линию поля, которая указывает на юг за пределами катушки (те, которые внесли свой вклад на своем пути на север, но на своем пути на юг), и вы представите, как размещаете катушку выше, в конечном итоге катушка и линия поля пересекаются, если вы поместите ее еще дальше , силовая линия теперь не может пробить область, ограниченную катушкой, так как вообще не вносит никакого магнитного потока.Итак, поток снижается. Каждая силовая линия имела такую точку, поэтому поток просто снижался, уменьшался и уменьшался по мере удаления катушки от магнита.

Вы можете сделать то же самое, сдвинув катушку вниз, но на этот раз линия поля пересекает плоскость катушки вне катушки на своем пути к южному полюсу стержневого магнита. Таким образом, результирующий эффект состоит в том, что поток тем слабее, чем дальше катушка от магнита, и когда магнит был центрирован на катушке, поток содержал все силовые линии, которые не вращались внутри катушки (они были у нее, но она они приходили и уходили, так что никакого чистого эффекта).И он становится только слабее этого.

Таким образом, когда катушка находится дальше от магнита, у вас меньше магнитного потока в области, ограниченной катушкой. Таким образом, мы ожидаем, что область под кривой ЭДС будет нулевой влево, а затем, когда вы представите себе перемещение вертикальной линии для $ t = T $ вправо, вы начнете получать все больше и больше площади слева от линии $ t. = T $ до тех пор, пока площадь не станет равной магнитному потоку площади, когда катушка центрирована на магните. Вот когда поток самый большой. В этот момент магнитный поток должен стать меньше, поскольку магнит продолжает двигаться.Мы можем уменьшить площадь, сказав, что область ниже линии $ y = 0 $ Вольт и выше кривой ЭДС считается отрицательной областью. Итак, нам нужно это получить, и в конечном итоге, когда стержневой магнит находится далеко, общий поток снова равен нулю, поэтому отрицательная область между кривой ЭДС и осью x (область под осью x и над кривой ЭДС) должна быть равняется положительной площади между кривой ЭДС и осью x (площадь под кривой x-эдс и над осью x), поэтому общая площадь равна нулю, чтобы магнитный поток был равен нулю.Как и должно быть в последнее время, т.е. далеко вправо.

Все, что нам осталось объяснить, это то, почему область справа более сжатая. Поскольку магнит падает, он ускоряется и падает все быстрее и быстрее, поэтому он быстро удаляется от центра позже, поэтому поток изменяется быстрее. Таким образом, нам нужно быстрее накапливать больше площади, поэтому нам нужна большая ЭДС, большая ЭДС дает больше площади за определенное время, например полоса площади между вертикальными линиями $ t = t_1 $ и $ t = t_2 $ содержит больше область, когда $ t_2-t_1 $ = 1 сек (в одну секунду), если ЭДС больше (и положительная область, если ЭДС положительная, и отрицательная область, если ЭДС отрицательная).Таким образом, последняя часть кривой должна выглядеть как сжатая версия первой части, но еще более сжатая ближе к правому краю.

Насколько я могу судить, это первый ответ, который не говорит о темпах изменений и объясняет причину каждого шага в терминах непрофессионала.

Технически, если вы хотите знать, в каком направлении идет ЭДС, вам нужно обратить внимание на то, роняете ли вы магнит северным полюсом вверх или северным полюсом вниз. Никакие идеи не меняются, кривые ЭДС в любом случае будут одинаковыми.

20.2 Электромагнитная индукция | Texas Gateway

Индуцированная электродвижущая сила

Если в катушке индуцируется ток, Фарадей рассуждал, что должно быть то, что он назвал электродвижущей силой , проталкивающей заряды через катушку. Эта интерпретация оказалась неверной; вместо этого внешний источник, выполняющий работу по перемещению магнита, добавляет энергию зарядам в катушке. Энергия, добавляемая на единицу заряда, измеряется в вольтах, поэтому электродвижущая сила на самом деле является потенциалом.К сожалению, название «электродвижущая сила» прижилось, а вместе с ним и возможность спутать его с реальной силой. По этой причине мы избегаем термина электродвижущая сила и просто используем сокращение эдс , которое имеет математический символ ε.ε. ЭДС может быть определена как скорость, с которой энергия отбирается от источника на единицу тока, протекающего по цепи. Таким образом, ЭДС — это энергия на единицу заряда , добавленная источником, которая контрастирует с напряжением, которое представляет собой энергию на единицу заряда , высвобождаемую , когда заряды проходят через цепь.

Чтобы понять, почему в катушке возникает ЭДС из-за движущегося магнита, рассмотрим рисунок 20.27, на котором показан стержневой магнит, движущийся вниз относительно проволочной петли. Первоначально через петлю проходят семь силовых линий магнитного поля (см. Изображение слева). Поскольку магнит удаляется от катушки, только пять силовых линий магнитного поля проходят через петлю за короткое время ΔtΔt (см. Изображение справа). Таким образом, когда происходит изменение количества силовых линий магнитного поля, проходящих через область, определяемую проволочной петлей, в проволочной петле индуцируется ЭДС.Подобные эксперименты показывают, что наведенная ЭДС пропорциональна скорости изменения магнитного поля. Математически мы выражаем это как

20.10ε∝ΔBΔt, ε∝ΔBΔt,

, где ΔBΔB — изменение величины магнитного поля за время ΔtΔt, а A — площадь петли.

Рис. 20.27 Стержневой магнит движется вниз относительно проволочной петли, так что количество силовых линий магнитного поля, проходящих через петлю, со временем уменьшается.Это вызывает в контуре ЭДС, создающую электрический ток.

Обратите внимание, что силовые линии магнитного поля, которые лежат в плоскости проволочной петли, на самом деле не проходят через петлю, как показано крайней левой петлей на рис. 20.28. На этом рисунке стрелка, выходящая из петли, представляет собой вектор, величина которого равна площади петли, а направление перпендикулярно плоскости петли. На рисунке 20.28 петля повернута от θ = 90 ° θ = 90 °. до θ = 0 °, θ = 0 ° вклад силовых линий магнитного поля в ЭДС увеличивается.Таким образом, для создания ЭДС в проволочной петле важна составляющая магнитного поля, которая составляет перпендикулярно плоскости петли, то есть Bcosθ.Bcosθ.

Это аналог паруса на ветру. Представьте, что проводящая петля — это парус, а магнитное поле — как ветер. Чтобы максимизировать силу ветра на парусе, парус ориентируют так, чтобы вектор его поверхности указывал в том же направлении, что и ветер, как в самой правой петле на рис. 20.28. Когда парус выровнен так, что его вектор поверхности перпендикулярен ветру, как в самой левой петле на рисунке 20.28, то ветер не действует на парус.

Таким образом, с учетом угла наклона магнитного поля к площади, пропорциональность E∝ΔB / ΔtE∝ΔB / Δt становится равной

20.11E∝ΔBcosθΔt.E∝ΔBcosθΔt. Рис. 20.28 Магнитное поле лежит в плоскости крайней левой петли, поэтому в этом случае оно не может генерировать ЭДС. Когда петля поворачивается так, что угол магнитного поля с вектором, перпендикулярным области петли, увеличивается до 90 ° 90 ° (см. Крайнюю правую петлю), магнитное поле вносит максимальный вклад в ЭДС в петле.Точки показывают, где силовые линии магнитного поля пересекают плоскость, определяемую петлей.

Другой способ уменьшить количество силовых линий магнитного поля, которые проходят через проводящую петлю на рисунке 20.28, — это не перемещать магнит, а сделать петлю меньше. Эксперименты показывают, что изменение площади проводящей петли в стабильном магнитном поле вызывает в петле ЭДС. Таким образом, ЭДС, создаваемая в проводящей петле, пропорциональна скорости изменения произведения перпендикулярного магнитного поля и площади петли

. 20.12ε∝Δ [(Bcosθ) A] Δt, ε∝Δ [(Bcosθ) A] Δt,

, где BcosθBcosθ — перпендикулярное магнитное поле, а A — площадь контура. Продукт BAcosθBAcosθ очень важен. Оно пропорционально количеству силовых линий магнитного поля, которые проходят перпендикулярно через поверхность площадью A . Возвращаясь к нашей аналогии с парусом, он будет пропорционален силе ветра на парусе. Он называется магнитным потоком и обозначается как ΦΦ.

20,13Φ = BAcosθΦ = BAcosθ

Единицей измерения магнитного потока является Вебер (Вб), который представляет собой магнитное поле на единицу площади, или Т / м ².Вебер — это также вольт-секунда (Vs).

Индуцированная ЭДС фактически пропорциональна скорости изменения магнитного потока через проводящую петлю.

20,14ε∝ΔΦΔtε∝ΔΦΔt

Наконец, для катушки, изготовленной из петель N , ЭДС в N раз сильнее, чем для одиночной петли. Таким образом, наведенная изменяющимся магнитным полем ЭДС в катушке из N петель составляет

ε∝NΔBcosθΔtA.ε∝NΔBcosθΔtA.

Последний вопрос, на который нужно ответить, прежде чем мы сможем преобразовать пропорциональность в уравнение: «В каком направлении течет ток?» Русский ученый Генрих Ленц (1804–1865) объяснил, что ток течет в том направлении, которое создает магнитное поле, которое пытается сохранить постоянный поток в контуре.Например, снова рассмотрим рисунок 20.27. Движение стержневого магнита приводит к уменьшению количества направленных вверх силовых линий магнитного поля, которые проходят через петлю. Следовательно, в контуре генерируется ЭДС, которая направляет ток в направлении, которое создает более направленные вверх силовые линии магнитного поля. Используя правило правой руки, мы видим, что этот ток должен течь в направлении, показанном на рисунке. Чтобы выразить тот факт, что наведенная ЭДС действует, чтобы противодействовать изменению магнитного потока через проволочную петлю, знак минус вводится в пропорциональность εΔΔΦ / Δtε introducedΔΦ / Δt, которая дает закон индукции Фарадея.) внутри катушки, направленной влево. Это будет противодействовать увеличению магнитного потока, направленного вправо. Чтобы увидеть, в каком направлении должен течь ток, направьте большой палец правой руки в желаемом направлении магнитного поля B → катушка, B → катушка, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки. Это показано изображением правой руки в верхнем ряду рисунка 20.29. Таким образом, ток должен течь в направлении, показанном на рисунке 4 (а).

На Рисунке 4 (b) направление движения магнита изменено на противоположное.В катушке направленное вправо магнитное поле B → magB → mag из-за движущегося магнита уменьшается. Закон Ленца гласит, что, чтобы противостоять этому уменьшению, ЭДС будет управлять током, который создает дополнительное направленное вправо магнитное поле B → катушка B → катушка в катушке. Опять же, направьте большой палец правой руки в желаемом направлении магнитного поля, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки (Рисунок 4 (b)).

Наконец, на Рисунке 4 (c) магнит перевернут, так что южный полюс находится ближе всего к катушке.Теперь магнитное поле B → magB → mag направлено на магнит, а не на катушку. Когда магнит приближается к катушке, он вызывает увеличение направленного влево магнитного поля в катушке. Закон Ленца гласит, что ЭДС, индуцированная в катушке, будет управлять током в направлении, которое создает магнитное поле, указывающее вправо. Это будет противодействовать увеличению магнитного потока, направленного влево из-за магнита. Повторное использование правила правой руки, как показано на рисунке, показывает, что ток должен течь в направлении, показанном на рисунке 4 (c).

Рис. 20.29 Закон Ленца гласит, что ЭДС, индуцированная магнитным полем, будет управлять током, который сопротивляется изменению магнитного потока в цепи. Это показано на панелях (а) — (с) для различных ориентаций и скоростей магнита. Правые руки справа показывают, как применить правило правой руки, чтобы найти, в каком направлении наведенный ток течет вокруг катушки.

Виртуальная физика

Электромагнитная лаборатория Фарадея

Это моделирование предлагает несколько действий.А пока щелкните вкладку Pickup Coil, которая представляет собой стержневой магнит, который вы можете перемещать через катушку. Когда вы это сделаете, вы увидите, как электроны движутся в катушке, и загорится лампочка, или вольтметр покажет напряжение на резисторе. Обратите внимание, что вольтметр позволяет вам видеть знак напряжения при перемещении магнита. Вы также можете оставить стержневой магнит в покое и переместить катушку, хотя наблюдать за результатами сложнее.

Проверка захвата

Сориентируйте стержневой магнит так, чтобы северный полюс был направлен вправо, и поместите катушку датчика справа от стержневого магнита.Теперь переместите стержневой магнит к катушке и посмотрите, в каком направлении движутся электроны. Это такая же ситуация, как показано ниже. Ток при моделировании течет в том же направлении, что и показано ниже? Объясните, почему да или почему нет.

Да, ток в моделировании течет в том же направлении, потому что направление тока противоположно направлению потока электронов.
Нет, ток в моделировании течет в противоположном направлении, потому что направление тока совпадает с направлением потока электронов.

Watch Physics

Индуцированный ток в проводе

В этом видео объясняется, как можно индуцировать ток в прямом проводе, перемещая его через магнитное поле. Лектор использует перекрестное произведение , тип векторного умножения. Не волнуйтесь, если вы не знакомы с этим, он в основном объединяет правило правой руки для определения силы, действующей на заряды в проводе, с уравнением F = qvBsinθ.F = qvBsinθ.

Проверка захвата

Какая ЭДС создается на прямом проводе 0.через однородное магнитное поле (0,30 Тл) ẑ ? Провод лежит в направлении 1 . Кроме того, какой конец провода имеет более высокий потенциал — пусть нижний конец провода находится под углом y = 0, а верхний конец — под углом y = 0,5 м)?

0,15 В и нижний конец провода будет иметь более высокий потенциал
0,15 В и на верхнем конце провода будет более высокий потенциал
0,075 В и нижний конец провода будет иметь более высокий потенциал
0.075 В и на верхнем конце провода будет более высокий потенциал

Рабочий пример

ЭДС, индуцированная в проводящей катушке движущимся магнитом

Представьте, что магнитное поле проходит через катушку в направлении, указанном на рисунке 20.31. Диаметр катушки 2,0 см. Если магнитное поле изменится с 0,020 до 0,010 Тл за 34 с, каковы направление и величина индуцированного тока? Предположим, что катушка имеет сопротивление 0,1 Ом.

Рисунок 20.31 Катушка, через которую проходит магнитное поле B .

СТРАТЕГИЯ

Используйте уравнение ε = −NΔΦ / Δtε = −NΔΦ / Δt, чтобы найти наведенную ЭДС в катушке, где Δt = 34 sΔt = 34 с. Подсчитав количество витков соленоида, мы находим, что у него 16 петель, поэтому N = 16.N = 16. Используйте уравнение Φ = BAcosθΦ = BAcosθ для расчета магнитного потока

20,16Φ = BAcosθ = Bπ (d2) 2, Φ = BAcosθ = Bπ (d2) 2,

, где d — диаметр соленоида, и мы использовали cos0 ° = 1. cos0 ° = 1. Поскольку площадь соленоида не меняется, изменение магнитного потока через соленоид составляет

20.17 ΔΦ = ΔBπ (d2) 2. ΔΦ = ΔBπ (d2) 2.

Найдя ЭДС, мы можем использовать закон Ома, ε = IR, ε = IR, чтобы найти ток.

Наконец, закон Ленца гласит, что ток должен создавать магнитное поле, которое препятствует уменьшению приложенного магнитного поля. Таким образом, ток должен создавать магнитное поле справа.

Решение

Объединение уравнений ε = −NΔΦ / Δtε = −NΔΦ / Δt и Φ = BAcosθΦ = BAcosθ дает

20,18ε = −NΔΦΔt = −NΔBπd24Δt.ε = −NΔΦΔt = −NΔBπd24Δt.

Решив закон Ома для тока и используя этот результат, получаем

20.19I = εR = −NΔBπd24RΔt = −16 (−0,010 Тл) π (0,020 м) 24 (0,10 Ом) (34 с) = 15 мкА.I = εR = −NΔBπd24RΔt = −16 (−0,010 Тл) π (0,020 м ) 24 (0,10 Ом) (34 с) = 15 мкА.

Закон Ленца гласит, что ток должен создавать магнитное поле вправо. Таким образом, мы направляем большой палец правой руки вправо и сжимаем пальцы правой руки вокруг соленоида. Ток должен течь в том направлении, в котором указывают наши пальцы, поэтому он входит в левый конец соленоида и выходит из правого конца.

Обсуждение

Давайте посмотрим, имеет ли смысл знак минус в законе индукции Фарадея.Определите направление магнитного поля как положительное. Это означает, что изменение магнитного поля отрицательное, как мы обнаружили выше. Знак минус в законе индукции Фарадея отрицает отрицательное изменение магнитного поля, оставляя нам положительный ток. Следовательно, ток должен течь в направлении магнитного поля, что мы и обнаружили.

Теперь попробуйте определить положительное направление как направление, противоположное направлению магнитного поля, то есть положительное направление находится слева на рисунке 20.31. В этом случае вы обнаружите отрицательный ток. Но поскольку положительное направление находится влево, отрицательный ток должен течь вправо, что снова согласуется с тем, что мы обнаружили с помощью закона Ленца.

Рабочий пример

Магнитная индукция из-за изменения размера цепи

Схема, показанная на рисунке 20.32, состоит из U-образного провода с резистором, концы которого соединены скользящим токопроводящим стержнем. Магнитное поле, заполняющее область, ограниченную контуром, имеет постоянное значение 0.01 T. Если стержень тянут вправо со скоростью v = 0,50 м / с, v = 0,50 м / с, какой ток индуцируется в цепи и в каком направлении он течет?

Рисунок 20.32 Схема ползунка. Магнитное поле постоянно, и шток тянется вправо со скоростью v . Изменяющаяся область, заключенная в цепи, вызывает в цепи ЭДС.

СТРАТЕГИЯ

Мы снова используем закон индукции Фарадея, E = −NΔΦΔt, E = −NΔΦΔt, хотя на этот раз магнитное поле остается постоянным и площадь, ограниченная контуром, изменяется.Схема состоит из одного контура, поэтому N = 1. N = 1. Скорость изменения площади ΔAΔt = vℓ.ΔAΔt = vℓ. Таким образом, скорость изменения магнитного потока составляет

20,20 ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ, ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ,

, где мы использовали тот факт, что угол θθ между вектором площади и магнитным полем равен 0 °. Зная ЭДС, мы можем найти ток, используя закон Ома. Чтобы найти направление тока, мы применяем закон Ленца.

Решение

Закон индукции Фарадея дает

20.21E = −NΔΦΔt = −Bvℓ.E = −NΔΦΔt = −Bvℓ.

Решение закона Ома для тока и использование предыдущего результата для ЭДС дает

20,22I = ER = −BvℓR = — (0,010 Тл) (0,50 м / с) (0,10 м) 20 Ом = 25 мкА.I = ER = −BvℓR = — (0,010 Тл) (0,50 м / с) (0,10 м ) 20 Ом = 25 мкА.

По мере того, как стержень скользит вправо, магнитный поток, проходящий через цепь, увеличивается. Закон Ленца говорит нам, что индуцированный ток создаст магнитное поле, которое будет противодействовать этому увеличению. Таким образом, магнитное поле, создаваемое индуцированным током, должно попадать на страницу.Сгибание петли пальцами правой руки по часовой стрелке заставляет большой палец правой руки указывать на страницу, что является желаемым направлением магнитного поля. Таким образом, ток должен течь по цепи по часовой стрелке.

Обсуждение

Сохраняется ли энергия в этой цепи? Внешний агент должен тянуть стержень с достаточной силой, чтобы просто уравновесить силу на проводе с током в магнитном поле — вспомните, что F = IℓBsinθ.F = IℓBsinθ. Скорость, с которой эта сила действует на стержень, должна уравновешиваться скоростью, с которой цепь рассеивает мощность.Используя F = IℓBsinθ, F = IℓBsinθ, сила, необходимая для протягивания проволоки с постоянной скоростью v , равна

. 20.23Fpull = IℓBsinθ = IℓB, Fpull = IℓBsinθ = IℓB,

, где мы использовали тот факт, что угол θθ между током и магнитным полем составляет 90 ° .90 °. Подставляя приведенное выше выражение для тока в это уравнение, получаем

20.24Fpull = IℓB = −BvℓR (ℓB) = — B2vℓ2R.Fpull = IℓB = −BvℓR (ℓB) = — B2vℓ2R.

Сила, создаваемая агентом, тянущим стержень, равна Fpullv, или Fpullv, или

. 20.25Ppull = Fpullv = −B2v2ℓ2R.Потяните = Fpullv = −B2v2ℓ2R.

Мощность, рассеиваемая схемой, составляет

. 20. 26Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R.Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R.

Таким образом, мы видим, что Ppull + Pdissipated = 0, Ppull + Pdissipated = 0, что означает, что мощность сохраняется в системе, состоящей из цепи и агента, который тянет стержень. Таким образом, в этой системе сохраняется энергия.

20.3 Электромагнитная индукция — физика

Изменение магнитных полей

В предыдущем разделе мы узнали, что ток создает магнитное поле.Если природа симметрична, то, возможно, магнитное поле может создать ток. В 1831 году, примерно через 12 лет после открытия, что электрический ток создает магнитное поле, английский ученый Майкл Фарадей (1791–1862) и американский ученый Джозеф Генри (1797–1878) независимо друг от друга продемонстрировали, что магнитные поля могут создавать токи. Основной процесс генерации токов с помощью магнитных полей называется индукцией; этот процесс также называют магнитной индукцией, чтобы отличить его от индукционной зарядки, в которой используется электростатическая кулоновская сила.

Когда Фарадей открыл то, что сейчас называется законом индукции Фарадея, королева Виктория спросила его, как можно использовать электричество. «Мадам, — ответил он, — что хорошего в ребенке?» Сегодня токи, индуцированные магнитными полями, необходимы нашему технологическому обществу. Электрогенератор, который можно найти во всем, от автомобилей до велосипедов и атомных электростанций, использует магнетизм для генерации электрического тока. Другие устройства, которые используют магнетизм для индукции токов, включают в себя звукосниматели в электрогитарах, трансформаторы любого размера, определенные микрофоны, ворота безопасности аэропорта и механизмы демпфирования на чувствительных химических весах.

Один из экспериментов Фарадея для демонстрации магнитной индукции заключался в том, чтобы переместить стержневой магнит через проволочную катушку и измерить результирующий электрический ток через проволоку. Схема этого эксперимента показана на рис. 20.33. Он обнаружил, что ток индуцируется только тогда, когда магнит движется относительно катушки. Когда магнит неподвижен по отношению к катушке, в катушке не индуцируется ток, как показано на рисунке 20.33. Кроме того, перемещение магнита в обратном направлении (сравните Рисунок 20.33 с рисунком 20.33) или смена полюсов магнита (сравните рис. 20.33 с рис. 20.33) приводит к возникновению тока в противоположном направлении.

Рисунок 20.33 Движение магнита относительно катушки создает электрические токи, как показано. Такие же токи возникают, если катушку перемещать относительно магнита. Чем больше скорость, тем больше величина тока, и ток равен нулю, когда нет движения. Ток, возникающий при перемещении магнита вверх, имеет направление, противоположное направлению тока, возникающего при перемещении магнита вниз.

Виртуальная физика

Закон Фарадея

Попробуйте это моделирование, чтобы увидеть, как движение магнита создает ток в цепи. Лампочка загорается, чтобы показать, когда течет ток, а вольтметр показывает падение напряжения на лампочке. Попробуйте переместить магнит через четырехвитковую катушку и через двухвитковую катушку. Какая катушка производит более высокое напряжение при одинаковой скорости магнита?

Проверка захвата

Если северный полюс находится влево и магнит перемещается справа налево, при входе магнита в катушку создается положительное напряжение.Какое знаковое напряжение получится, если эксперимент повторить с южным полюсом слева?

Знак напряжения изменится, потому что направление тока изменится при перемещении южного полюса магнита влево.
Знак напряжения останется прежним, потому что направление тока не изменится при перемещении южного полюса магнита влево.
Знак напряжения изменится, потому что величина протекающего тока изменится при перемещении южного полюса магнита влево.
Знак напряжения останется прежним, потому что величина тока не изменится при перемещении южного полюса магнита влево.

Индуцированная электродвижущая сила

Если в катушке индуцируется ток, Фарадей рассуждал, что должно быть то, что он назвал электродвижущей силой , проталкивающей заряды через катушку. Эта интерпретация оказалась неверной; вместо этого внешний источник, выполняющий работу по перемещению магнита, добавляет энергию зарядам в катушке.Энергия, добавляемая на единицу заряда, измеряется в вольтах, поэтому электродвижущая сила на самом деле является потенциалом. К сожалению, название «электродвижущая сила» прижилось, а вместе с ним и возможность спутать его с реальной силой. По этой причине мы избегаем термина электродвижущая сила и просто используем сокращение эдс , которое имеет математический символ ε.ε. ЭДС может быть определена как скорость, с которой энергия отбирается от источника на единицу тока, протекающего по цепи. Таким образом, ЭДС — это энергия на единицу заряда , добавленная источником, которая контрастирует с напряжением, которое представляет собой энергию на единицу заряда , высвобождаемую , когда заряды проходят через цепь.

Чтобы понять, почему в катушке возникает ЭДС из-за движущегося магнита, рассмотрим рисунок 20.34, на котором показан стержневой магнит, движущийся вниз относительно проволочной петли. Первоначально через петлю проходят семь силовых линий магнитного поля (см. Изображение слева). Поскольку магнит удаляется от катушки, только пять силовых линий магнитного поля проходят через петлю за короткое время ΔtΔt (см. Изображение справа). Таким образом, когда происходит изменение количества силовых линий магнитного поля, проходящих через область, определяемую проволочной петлей, в проволочной петле индуцируется ЭДС.Подобные эксперименты показывают, что наведенная ЭДС пропорциональна скорости изменения магнитного поля. Математически мы выражаем это как

ε∝ΔBΔt, ε∝ΔBΔt,

20,24

где ΔBΔB — изменение величины магнитного поля за время ΔtΔt, а A — площадь петли.

Рис. 20.34 Стержневой магнит движется вниз относительно проволочной петли, так что количество силовых линий магнитного поля, проходящих через петлю, со временем уменьшается.Это вызывает в контуре ЭДС, создающую электрический ток.

Обратите внимание, что силовые линии магнитного поля, которые лежат в плоскости проволочной петли, на самом деле не проходят через петлю, как показано крайней левой петлей на рис. 20.35. На этом рисунке стрелка, выходящая из петли, представляет собой вектор, величина которого равна площади петли, а направление перпендикулярно плоскости петли. На рисунке 20.35 петля повернута от θ = 90 ° θ = 90 °. до θ = 0 °, θ = 0 ° вклад силовых линий магнитного поля в ЭДС увеличивается.Таким образом, для создания ЭДС в проволочной петле важна составляющая магнитного поля, которая составляет перпендикулярно плоскости петли, то есть Bcosθ.Bcosθ.

Это аналог паруса на ветру. Представьте, что проводящая петля — это парус, а магнитное поле — как ветер. Чтобы максимизировать силу ветра на парусе, парус ориентируют так, чтобы вектор его поверхности указывал в том же направлении, что и ветер, как в самой правой петле на рис. 20.35. Когда парус выровнен так, что его вектор поверхности перпендикулярен ветру, как в самой левой петле на рисунке 20.35, то ветер не действует на парус.

Таким образом, с учетом угла наклона магнитного поля по отношению к площади, пропорциональность E∝ΔB / ΔtE∝ΔB / Δt становится равной

E∝ΔBcosθΔt.E∝ΔBcosθΔt.

20,25

Рис. 20.35 Магнитное поле лежит в плоскости крайней левой петли, поэтому в этом случае оно не может генерировать ЭДС. Когда петля поворачивается так, что угол магнитного поля с вектором, перпендикулярным области петли, увеличивается до 90 ° 90 ° (см. Крайнюю правую петлю), магнитное поле вносит максимальный вклад в ЭДС в петле.Точки показывают, где силовые линии магнитного поля пересекают плоскость, определяемую петлей.

Еще один способ уменьшить количество силовых линий магнитного поля, которые проходят через проводящую петлю на рис. 20.35, — это не перемещать магнит, а сделать петлю меньше. Эксперименты показывают, что изменение площади проводящей петли в стабильном магнитном поле вызывает в петле ЭДС. Таким образом, ЭДС, создаваемая в проводящей петле, пропорциональна скорости изменения произведения перпендикулярного магнитного поля и площади петли

. ε∝Δ [(Bcosθ) A] Δt, ε∝Δ [(Bcosθ) A] Δt,

20.26

Φ = BAcosθΦ = BAcosθ

20,27

Единицей измерения магнитного потока является Вебер (Вб), то есть магнитное поле на единицу площади, или Т / м ².Вебер — это также вольт-секунда (Vs).

ε∝ΔΦΔtε∝ΔΦΔt

20,28

ε∝NΔBcosθΔtA.ε∝NΔBcosθΔtA.

Последний вопрос, на который нужно ответить, прежде чем мы сможем преобразовать пропорциональность в уравнение: «В каком направлении течет ток?» Русский ученый Генрих Ленц (1804–1865) объяснил, что ток течет в том направлении, которое создает магнитное поле, которое пытается сохранить постоянный поток в контуре.Например, снова рассмотрим рисунок 20.34. Движение стержневого магнита приводит к уменьшению количества направленных вверх силовых линий магнитного поля, которые проходят через петлю. Следовательно, в контуре генерируется ЭДС, которая направляет ток в направлении, которое создает более направленные вверх силовые линии магнитного поля. Используя правило правой руки, мы видим, что этот ток должен течь в направлении, показанном на рисунке. Чтобы выразить тот факт, что наведенная ЭДС действует как противодействие изменению магнитного потока через проволочную петлю, в пропорциональность ε∝ΔΦ / Δt вводится знак минус.) внутри катушки, направленной влево. Это будет противодействовать увеличению магнитного потока, направленного вправо. Чтобы увидеть, в каком направлении должен течь ток, направьте большой палец правой руки в желаемом направлении магнитного поля B → катушка, B → катушка, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки. Это показано изображением правой руки в верхнем ряду рисунка 20.36. Таким образом, ток должен течь в направлении, показанном на рисунке 4 (а).

Рис. 20.36. Закон Ленца гласит, что ЭДС, индуцированная магнитным полем, будет управлять током, который сопротивляется изменению магнитного потока в цепи. Это показано на панелях (а) — (с) для различных ориентаций и скоростей магнита. Правые руки справа показывают, как применить правило правой руки, чтобы найти, в каком направлении наведенный ток течет вокруг катушки.

Виртуальная физика

Электромагнитная лаборатория Фарадея

Контроль захвата

Да, ток в моделировании течет, как показано, потому что направление тока противоположно направлению потока электронов.
Нет, ток в моделировании течет в противоположном направлении, потому что направление тока совпадает с направлением потока электронов.

Watch Physics

Индуцированный ток в проводе

Контроль захвата

0,15 В и нижний конец провода будет иметь более высокий потенциал
0,15 В и на верхнем конце провода будет более высокий потенциал
0,075 В и нижний конец провода будет иметь более высокий потенциал
0.075 В и на верхнем конце провода будет более высокий потенциал

Рабочий пример

ЭДС, индуцированная в проводящей катушке движущимся магнитом

Представьте, что магнитное поле проходит через катушку в направлении, указанном на рисунке 20.37. Диаметр катушки 2,0 см. Если магнитное поле изменится с 0,020 до 0,010 Тл за 34 с, каковы направление и величина индуцированного тока? Предположим, что катушка имеет сопротивление 0,1 Ом.

Рисунок 20.37 Катушка, через которую проходит магнитное поле B .

Стратегия

Используйте уравнение ε = −NΔΦ / Δtε = −NΔΦ / Δt, чтобы найти наведенную ЭДС в катушке, где Δt = 34sΔt = 34s. Подсчитав количество витков соленоида, мы находим, что у него 16 петель, поэтому N = 16.N = 16. Используйте уравнение Φ = BAcosθΦ = BAcosθ для расчета магнитного потока

Φ = BAcosθ = Bπ (d2) 2, Φ = BAcosθ = Bπ (d2) 2,

20,30

, где d — диаметр соленоида, а мы использовали cos0 ° = 1. cos0 ° = 1. Поскольку площадь соленоида не меняется, изменение магнитного потока через соленоид составляет

ΔΦ = ΔBπ (d2) 2.ΔΦ = ΔBπ (d2) 2.

20,31

Найдя ЭДС, мы можем использовать закон Ома, ε = IR, ε = IR, чтобы найти ток.

Решение

Объединение уравнений ε = −NΔΦ / Δtε = −NΔΦ / Δt и Φ = BAcosθΦ = BAcosθ дает

ε = −NΔΦΔt = −NΔBπd24Δt.ε = −NΔΦΔt = −NΔBπd24Δt.

20,32

Решение закона Ома для тока и использование этого результата дает

I = εR = −NΔBπd24RΔt = −16 (−0,010T) π (0,020 м) 24 (0,10 Ом) (34 с) = 15 мкА.I = εR = −NΔBπd24RΔt = −16 (−0,010T) π (0,020 м) 24 (0,10 Ом) (34 с) = 15 мкА.

20.33

Закон Ленца гласит, что ток должен создавать магнитное поле справа. Таким образом, мы направляем большой палец правой руки вправо и сжимаем пальцы правой руки вокруг соленоида. Ток должен течь в том направлении, в котором указывают наши пальцы, поэтому он входит в левый конец соленоида и выходит из правого конца.

Обсуждение

Давайте посмотрим, имеет ли смысл знак минус в законе индукции Фарадея. Определите направление магнитного поля как положительное. Это означает, что изменение магнитного поля отрицательное, как мы обнаружили выше. Знак минус в законе индукции Фарадея отрицает отрицательное изменение магнитного поля, оставляя нам положительный ток. Следовательно, ток должен течь в направлении магнитного поля, что мы и обнаружили.

Теперь попробуйте определить положительное направление как направление, противоположное направлению магнитного поля, то есть положительное направление находится слева на рисунке 20.37. В этом случае вы обнаружите отрицательный ток. Но поскольку положительное направление находится влево, отрицательный ток должен течь вправо, что снова согласуется с тем, что мы обнаружили с помощью закона Ленца.

Рабочий пример

Магнитная индукция из-за изменения размера цепи

Схема, показанная на рисунке 20.38, состоит из U-образного провода с резистором, концы которого соединены скользящим токопроводящим стержнем. Магнитное поле, заполняющее область, ограниченную контуром, имеет постоянное значение 0.01 T. Если стержень тянут вправо со скоростью v = 0,50 м / с, v = 0,50 м / с, какой ток индуцируется в цепи и в каком направлении он течет?

Рисунок 20.38 Схема ползунка. Магнитное поле постоянно, и шток тянется вправо со скоростью v . Изменяющаяся область, заключенная в цепи, вызывает в цепи ЭДС.

Стратегия

Мы снова используем закон индукции Фарадея, E = −NΔΦΔt, E = −NΔΦΔt, хотя на этот раз магнитное поле остается постоянным и площадь, ограниченная контуром, изменяется.Схема состоит из одного контура, поэтому N = 1.N = 1. Скорость изменения площади ΔAΔt = vℓ.ΔAΔt = vℓ. Таким образом, скорость изменения магнитного потока составляет

ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ, ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ,

20,34

Решение

Закон индукции Фарадея дает

E = −NΔΦΔt = −Bvℓ.E = −NΔΦΔt = −Bvℓ.

20,35

Решение закона Ома для тока и использование предыдущего результата для ЭДС дает

I = ER = −BvℓR = — (0,010T) (0,50 м / с) (0,10 м) 20Ω = 25 мкA I = ER = −BvℓR = — (0,010T) (0,50 м / с) (0,10 м) 20Ω = 25 мкА.

20,36

По мере скольжения стержня вправо магнитный поток, проходящий через контур, увеличивается. Закон Ленца говорит нам, что индуцированный ток создаст магнитное поле, которое будет противодействовать этому увеличению. Таким образом, магнитное поле, создаваемое индуцированным током, должно попадать на страницу.Сгибание петли пальцами правой руки по часовой стрелке заставляет большой палец правой руки указывать на страницу, что является желаемым направлением магнитного поля. Таким образом, ток должен течь по цепи по часовой стрелке.

Обсуждение

. Fpull = IℓBsinθ = IℓB, Fpull = IℓBsinθ = IℓB,

20,37

, где мы использовали тот факт, что угол θθ между током и магнитным полем составляет 90 ° 0,90 °. Подставляя приведенное выше выражение для тока в это уравнение, получаем

Fpull = IℓB = −BvℓR (ℓB) = — B2vℓ2R. Fpull = IℓB = −BvℓR (ℓB) = — B2vℓ2R.

20,38

Сила, создаваемая агентом, тянущим стержень, равна Fpullv, или Fpullv, или

. Потяните = Fpullv = −B2v2ℓ2R.Потяните = Fpullv = −B2v2ℓ2R.

20,39

Мощность, рассеиваемая схемой, составляет

Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R. Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R.

20,40

Электродвигатели и генераторы

Введение с использованием анимации и схем для объяснения физических принципов некоторых различных типов электродвигателей, генераторов, генераторов переменного тока, линейные двигатели и громкоговорители.

Двигатели постоянного тока

Простой двигатель постоянного тока имеет катушку с проволокой, которая может вращаться в магнитном поле. В ток в катушке подается через две щетки, которые обеспечивают подвижный контакт с разрезное кольцо. Катушка находится в постоянном магнитном поле. Силы приложили на токоведущих проводах создают крутящий момент на катушке. Сила F на проводе длиной L, по которому течет ток i в магнитном поле. B равно iLB, умноженному на синус угла между B и i, который будет равен 90 °, если поля были равномерно вертикальными.Направление F идет справа ручное правило, как показано здесь. Две силы, показанные здесь, равны и противоположны, но они смещены вертикально, поэтому создают крутящий момент. (Силы на две другие стороны катушки действуют по одной и той же линии и поэтому не создают крутящего момента.)

Катушку также можно рассматривать как магнитный диполь или небольшой электромагнит, как указано стрелкой SN: согните пальцы правой руки в направление течения, а большой палец — северный полюс.В эскизе Справа изображен электромагнит, образованный катушкой ротора. как постоянный магнит, и тот же крутящий момент (север притягивает юг) действовать для выравнивания центрального магнита.

Обратите внимание на влияние щеток на разрезное кольцо . Когда плоскость вращающейся катушки достигает горизонтали, щетки разорвут контакт (теряется не так много, потому что это точка нулевого момента все равно — силы действовать внутрь).Угловой момент катушки переносит ее через этот разрыв. точка, и ток затем течет в противоположном направлении, что меняет направление магнитный диполь. Итак, после прохождения точки останова ротор продолжает движение. повернуть против часовой стрелки и начать выравнивание в обратном направлении. в В следующем тексте я буду в основном использовать картинку «крутящий момент на магните», но имейте в виду, что использование щеток или переменного тока может привести к появлению полюсов электромагнит, о котором идет речь, меняет положение, когда ток меняет направление.

Крутящий момент, создаваемый в течение цикла, зависит от вертикального разделения две силы. Следовательно, это зависит от синуса угла между ось катушки и поле. Однако из-за разрезного кольца оно всегда в том же смысле. Анимация ниже показывает его изменение во времени, а вы можно остановить на любом этапе и проверить направление, приложив правую руку правило.

Двигатели и генераторы

Теперь двигатель постоянного тока также является генератором постоянного тока.Взгляните на следующую анимацию. В катушка, разрезное кольцо, щетки и магнит — это то же оборудование, что и двигатель выше, но катушка вращается, что генерирует ЭДС.

Если вы используете механическую энергию для вращения катушки (N витков, область A) с равномерным угловая скорость ω в магнитном поле B , это создаст в катушке синусоидальную ЭДС. ЭДС (ЭДС или электродвижущая сила — это почти то же самое, что и напряжение).Пусть θ будет угол между B и нормалью к катушке, поэтому магнитный поток φ равен NAB.cos θ. Закон Фарадея дает:

Приведенную выше анимацию можно назвать генератором постоянного тока. Как и в двигателе постоянного тока, концы катушки соединяются с разрезным кольцом, две половины которого контактируют кистями. Обратите внимание, что щетки и разрезное кольцо «исправляют» создаваемую ЭДС: контакты организованы так, что ток всегда будет течь в одном и том же направление, потому что, когда катушка проходит мимо мертвой точки, где щетки встречаются зазор в кольце, соединения между концами катушки и внешние клеммы перевернуты.ЭДС здесь (без учета мертвой зоны, которая обычно бывает при нулевом напряжении) равна | НБА ω sin ωt |, как нарисовано.

Генератор

Если нам нужен AC, нам не нужно исправление, поэтому нам не нужны разрезные кольца. ( Этот это хорошая новость, потому что разрезные кольца вызывают искры, озон, радиопомехи и дополнительный износ. Если ты хочешь Постоянного тока, часто лучше использовать генератор и выпрямлять диоды.)

В следующей анимации две кисти соприкасаются с двумя непрерывными кольцами, поэтому две внешние клеммы всегда подключены к одним и тем же концам катушки.Результатом является не исправленная синусоидальная ЭДС, определяемая NBAω sin ωt, который показан на следующей анимации.

Это генератор переменного тока. Преимущества переменного и постоянного тока генераторы сравниваются в разделе ниже. Выше мы видели, что двигатель постоянного тока также является генератором постоянного тока. Точно так же генератор переменного тока также является двигателем переменного тока. Тем не мение, это довольно негибкий. (Смотри как настоящие электродвигатели работают для более подробной информации.)

Задняя ЭДС

Теперь, как показывают первые две анимации, двигатели и генераторы постоянного тока могут быть то же самое. Например, двигатели поездов становятся генераторами, когда поезд замедляется: они преобразуют кинетическую энергию в электрическую и мощность обратно в сеть. В последнее время несколько производителей начали производить легковые автомобили. рационально. В таких автомобилях электродвигатели, используемые для привода автомобиля, также используется для зарядки аккумуляторов при остановке автомобиля — это называется регенеративным торможение.

Итак, вот интересное следствие. Каждый двигатель — это генератор . Это правда, в некотором смысле, даже когда он функционирует как двигатель. ЭДС, что мотор генерирует называется обратной ЭДС . Обратная ЭДС увеличивается с увеличением скорость из-за закона Фарадея. Итак, если двигатель не нагружен, он очень сильно крутится. быстро и разгоняется до появления обратной ЭДС плюс падение напряжения из-за потерь, равно напряжению питания. Обратную ЭДС можно рассматривать как «регулятор»: он останавливает двигатель, вращающийся бесконечно быстро (что избавляет физиков от некоторого затруднения).Когда двигатель нагружен, то фаза напряжения становится ближе к фазе тока (начинает выглядят резистивными), и это кажущееся сопротивление дает напряжение. Итак, спина Требуемая ЭДС меньше, и двигатель вращается медленнее. (Чтобы добавить обратно ЭДС, которая является индуктивной, к резистивной составляющей необходимо добавить напряжения которые не в фазе. См. AC схем.)

Катушки обычно имеют сердечники

На практике (и в отличие от схем, которые мы нарисовали) генераторы и постоянный ток двигатели часто имеют сердечник с высокой проницаемостью внутри катушки, так что большие магнитные поля создаются умеренными токами.Это показано слева в рисунок ниже, на котором статоры (статические магниты) постоянные магниты.

Моторы универсальные

Магниты статора также могут быть выполнены в виде электромагнитов, как показано выше. справа. Два статора намотаны в одном направлении, чтобы поле в том же направлении, а у ротора есть поле, которое дважды меняет направление за цикл, потому что он подключен к щеткам, которые здесь не указаны.Один Преимущество наличия статоров в двигателе состоит в том, что можно сделать двигатель который работает от переменного или постоянного тока, так называемый универсальный двигатель . Когда вы едете у такого мотора с переменным током ток в катушке меняется дважды за каждый цикл (помимо изменений со щеток), а вот полярность статоров изменяется одновременно, поэтому эти изменения аннулируются. (К сожалению, кисти еще остались, хотя я спрятал их в этом наброске.) За преимущества и недостатки постоянного магнита по сравнению со статорами с обмоткой см. ниже. Также смотрите больше на универсальных моторах.

Построить простой двигатель

Чтобы построить этот простой, но странный мотор, вам понадобятся два довольно сильных магнита. (подойдут редкоземельные магниты диаметром около 10 мм, магниты), жёсткий медный провод (не менее 50 см), два провода с крокодилом зажимы на обоих концах, фонарь на шесть вольт, две банки для безалкогольных напитков, два блока дерева, липкой ленты и острого гвоздя.

Сделайте катушку из жесткого медного провода, чтобы не было необходимости во внешних служба поддержки. Намотайте от 5 до 20 витков по кругу диаметром около 20 мм и два конца радиально направлены наружу в противоположных направлениях. Эти цели будут быть одновременно осью и контактами. Если провод имеет лаковую или пластиковую изоляцию, снимите его на концах.

Опоры оси могут быть выполнены из алюминия, поэтому что они создают электрический контакт.Например, проткнуть безалкогольный напиток банки с гвоздем, как показано. Расположите два магнита с севера на юг, так что магнитное поле проходит через катушку под прямым углом к оси. Заклейте или приклейте магниты к деревянным блокам (не показаны на схеме), чтобы они оставались на нужной высоте, затем переместите блоки поставить их на место, достаточно близко к катушке. Сначала поверните катушку так что магнитный поток через катушку равен нулю, как показано на схеме.

Теперь возьмем аккумулятор и два провода с зажимами типа «крокодил». Соединять два вывода батареи к двум металлическим опорам для катушка и она должна повернуться.

Обратите внимание, что у этого двигателя есть как минимум одна «мертвая зона»: он часто останавливается. в положении, когда на катушке отсутствует крутящий момент. Не уходи он горит слишком долго: он быстро разряжает аккумулятор.

Оптимальное количество витков в катушке зависит от внутреннего сопротивление аккумулятора, качество опорных контактов и тип провода, поэтому вам следует поэкспериментировать с разными значениями.

Как уже говорилось выше, это тоже генератор, но очень неэффективный. Чтобы увеличить ЭДС, используйте больше витков (может потребоваться использовать более тонкую проволоку и рамку для намотки.) Вы можете использовать например, электродрель, чтобы быстро ее повернуть, как показано на рисунке выше. Воспользуйтесь осциллографом, чтобы посмотреть на генерируемую ЭДС. Это переменный или постоянный ток?

У этого двигателя нет разъемного кольца, почему он работает на DC? Проще говоря, если бы он был точно симметричным, это не сработало бы.Однако, если ток в одном полупериоде немного меньше, чем в другом, то средний крутящий момент не будет равен нулю, и, поскольку он вращается достаточно быстро, угловой момент, приобретенный во время полупериода с большим током, переносит его через полупериод, когда крутящий момент находится в противоположном направлении. По крайней мере, два эффекта могут вызвать асимметрию. Даже если провода полностью зачищены и чистые, контактное сопротивление вряд ли будет одинаковым даже в состоянии покоя. Кроме того, само вращение вызывает прерывистый контакт, поэтому, если во время одной фазы есть более длительные отскоки, этой асимметрии будет достаточно.В принципе, вы можете частично зачистить провода таким образом, чтобы ток был равен нулю за один полупериод.

Альтернативная версия простого двигателя Джеймса Тейлор.

Еще более простой двигатель (который также намного проще для понимания!) — это униполярный двигатель.

Двигатели переменного тока

С помощью переменного тока мы можем изменить направление поля без использования щеток.Это хорошие новости, потому что мы можем избежать дуги, образования озона и омическая потеря энергии, которую могут повлечь за собой щетки. Далее, потому что кисти контактируют между движущимися поверхностями, они изнашиваются.

Первое, что нужно сделать в двигателе переменного тока, — это создать вращающееся поле. ‘Обычный’ Переменный ток от 2-х или 3-х контактной розетки — это однофазный переменный ток — он имеет одну синусоидальную разность потенциалов создается только между двумя проводами — активным и нейтральным. (Обратите внимание, что заземляющий провод не пропускает ток, за исключением электрические неисправности.) При однофазном переменном токе можно создать вращающееся поле. за счет генерации двух противофазных токов с помощью, например, конденсатора. В показанном примере два тока сдвинуты по фазе на 90 °, поэтому вертикальный составляющая магнитного поля синусоидальная, а горизонтальная косусоидальная, как показано. Это дает поле, вращающееся против часовой стрелки.

(* Меня попросили объяснить это: из простого AC Теоретически, ни катушки, ни конденсаторы не имеют напряжения в фазе с электрический ток.В конденсаторе напряжение максимально, когда заряд закончил течь на конденсатор и вот-вот начнет стекать. Таким образом, напряжение отстает от тока. В чисто индуктивной катушке падение напряжения является наибольшим, когда ток изменяется наиболее быстро, что также когда ток равен нулю. Напряжение (падение) опережает ток. В моторных катушках фазовый угол меньше 90, потому что электрические энергия преобразуется в механическую энергию.)

На этой анимации графики показывают изменение токов во времени. в вертикальной и горизонтальной катушках. График компонент поля B _x и B _y показывает, что векторная сумма этих двух полей является вращающейся поле. Основное изображение показывает вращающееся поле. Он также показывает полярность магнитов: как указано выше, синий представляет северный полюс, а красный — южный полюс.

Если мы поместим постоянный магнит в эту область вращающегося поля, или если мы положим в катушке, ток которой всегда течет в одном и том же направлении, тогда это становится Синхронный двигатель . В широком диапазоне условий двигатель будет повернуть со скоростью магнитного поля. Если у нас много статоров, вместо этого всего двух пар, показанных здесь, то мы могли бы рассматривать его как шаговый двигатель: каждый импульс перемещает ротор на следующую пару задействованных полюсов.Пожалуйста, помните мое предупреждение об идеализированной геометрии: настоящие шаговые двигатели десятки полюсов и довольно сложные геометрические формы!

Асинхронные двигатели

Теперь, поскольку у нас есть изменяющееся во времени магнитное поле, мы можем использовать наведенную ЭДС в катушке — или даже просто вихревые токи в проводнике — чтобы ротор магнит. Правильно, если у вас есть вращающееся магнитное поле, вы можете просто вставил проводник и получается.Это дает несколько преимуществ асинхронные двигатели : отсутствие щеток или коммутатора означает более простое производство, нет износ, отсутствие искр, отсутствие образования озона и отсутствие связанных с этим потерь энергии с ними. Слева внизу схематическое изображение асинхронного двигателя. (Для фотографий настоящие асинхронные двигатели и более подробную информацию см. в разделе Индукция. двигатели.)

Анимация справа представляет двигатель с короткозамкнутым ротором .Белка клетка имеет (во всяком случае, в этой упрощенной геометрии!) два круглых проводника, соединенных несколькими прямыми стержнями. Любые два стержня и соединяющие их дуги образуют катушка — на что указывают синие черточки на анимации. (Только два из для простоты показано много возможных схем.)

На этой схеме показано, почему их можно назвать двигателями с короткозамкнутым ротором. Реальность иная: фотографии и подробности см. В разделе «Индукция». моторы.Проблема с показанными асинхронными двигателями и двигателями с короткозамкнутым ротором в этой анимации показано, что конденсаторы высокой стоимости и высокого напряжения стоят дорого. Одним из решений является двигатель с экранированным полюсом, но его вращающийся поле имеет некоторые направления, в которых крутящий момент небольшой, и имеет тенденцию бежать назад при некоторых условиях. Самый простой способ избежать этого — использовать многофазные двигатели.

Трехфазные асинхронные двигатели переменного тока

Однофазный используется в домашних условиях для приложений с низким энергопотреблением, но у него есть недостатки.Во-первых, он выключается 100 раз в секунду (вы не обратите внимание, что флуоресцентные лампы мигают с такой скоростью, потому что ваши глаза слишком медленные: даже 25 изображений в секунду на экране телевизора достаточно, чтобы дать иллюзию непрерывного движения.) Во-вторых, это делает его неудобным для создания вращающихся магнитных полей. По этой причине некоторая высокая мощность (несколько кВт) для бытовых устройств может потребоваться трехфазная установка. Промышленное применение широко использовать трехфазный двигатель, трехфазный асинхронный двигатель является стандартным рабочая лошадка для приложений большой мощности.Три провода (не считая земли) несут три возможных разности потенциалов, которые не совпадают по фазе с каждым другое на 120 °, как показано на анимации ниже. Таким образом, три статора плавно вращающееся поле. (Посмотри это ссылку для получения дополнительной информации о трехфазном питании.)

Если поместить постоянный магнит в такой набор статоров, он станет синхронным. трехфазный двигатель .На анимации изображена беличья клетка, в которой простота показана только одна из многих петель наведенного тока. Без механической нагрузки, он вращается практически синхронно с вращающимся полем. Ротор не обязательно должен быть беличьей клеткой: на самом деле любой проводник, который переносимые вихревые токи будут вращаться, стремясь следовать за вращающимся полем. Такая компоновка может дать асинхронный двигатель , обладающий высоким КПД, высокая мощность и высокие крутящие моменты в диапазоне скоростей вращения.

Двигатели линейные

Набор катушек можно использовать для создания магнитного поля, которое переводит, скорее, чем вращается. На паре катушек на анимации ниже подается импульс от слева направо, поэтому область магнитного поля перемещается слева направо. А постоянный или электромагнит будет стремиться следовать за полем. Так что простой плита из проводящего материала, потому что в ней наведены вихревые токи (не показаны) содержат электромагнит. В качестве альтернативы мы могли бы сказать, что из Фарадея закон, ЭДС в металлической плите всегда индуцируется, чтобы противодействовать любому изменению в магнитном потоке, а силы на токах, вызванные этой ЭДС, сохраняют поток в плите почти постоянный.(Вихревые токи на этой анимации не показаны.)

В качестве альтернативы мы могли бы иметь комплекты катушек с питанием в подвижной части, и наводить вихревые токи в рельсе. В любом случае получается линейный двигатель, который был бы полезен, скажем, для поездов на магнитной подвеске. (В анимации геометрия как обычно на этом сайте, в высшей степени идеализирован, и только один вихретоковый ток показано.)

Некоторые примечания к двигателям переменного и постоянного тока для приложений большой мощности

Этот сайт изначально был написан в помощь старшеклассникам. и учителя в Новом Южном Уэльсе, Австралия, где в новой программе по истории и приложениям физики за счет самой физики, был введен.В новой программе в одной из точечных точек указано следующее: озадачивающее требование: «объясните, что двигатели переменного тока обычно производят малую мощность и связывают это с их использованием в электроинструментах «. Двигатели переменного тока используются для приложений с большой мощностью, когда это возможно. Три фазные асинхронные двигатели переменного тока широко используются для приложений большой мощности, в том числе тяжелая индустрия. Однако такие двигатели не подходят, если многофазность недоступна, или трудно доставить.Электропоезда тому пример: строить проще линии электропередач и пантографы, если нужен только один активный проводник, так что это обычно имеет постоянный ток, и многие двигатели поездов работают на постоянном токе. Однако из-за недостатков постоянного тока для высокой мощности, более современные поезда преобразуют постоянный ток в переменный, а затем бегут трехфазные двигатели.

Однофазные асинхронные двигатели имеют проблемы при объединении приложений высокая мощность и гибкие условия нагрузки. Проблема заключается в создании вращающееся поле.Конденсатор может использоваться для подачи тока в один набор впереди катушки, но дорогие высоковольтные конденсаторы стоят дорого. Затененный Вместо них используются полюсы, но крутящий момент на некоторых углах невелик. Если нельзя создают плавно вращающееся поле, и если груз «проскальзывает» далеко за поле, то крутящий момент падает или даже меняется на противоположное.

В электроинструментах и некоторых приборах используются щеточные электродвигатели переменного тока. Кисти вводят потери (плюс образование дуги и озона).Полярность статора изменена. 100 раз в секунду. Даже если материал сердечника выбран так, чтобы минимизировать гистерезис потерь («потери в железе»), это способствует неэффективности и возможности перегрева. Эти моторы можно назвать универсальными. двигатели, потому что они могут работать на постоянном токе. Это дешевое, но грубое решение. и неэффективно. Для приложений с относительно низким энергопотреблением, таких как электроинструменты, неэффективность обычно экономически не важна.

Если доступен только однофазный переменный ток, можно исправить переменный ток и использовать Двигатель постоянного тока. Раньше сильноточные выпрямители были дорогими, но сейчас они становятся все более дорогими. менее дорогой и более широко используемый. Если вы уверены, что понимаете принципы, пора перейти к разделу «Как настоящие электродвигатели работают Джона Стори. Или продолжайте здесь, чтобы найти о громкоговорителях и трансформаторах.

Громкоговорители

Громкоговоритель — это линейный двигатель с небольшим диапазоном.Имеет одинарное перемещение катушка, которая постоянно, но гибко подключена к источнику напряжения, поэтому кистей нет.

катушка движется в поле постоянного магнита, который обычно имеет форму для создания максимального усилия на катушке. Подвижная катушка не имеет сердечника, поэтому его масса невелика, и он может быстро ускоряться, что позволяет частота движения.В громкоговорителе катушка прикреплена к легкому весу. бумажный конус, который поддерживается на внутреннем и внешнем краях круглыми, плиссированные бумажные «пружины». На фотографии ниже динамик выходит за рамки нормальный верхний предел его перемещения, поэтому катушка видна над полюса магнита.

Для низкочастотного звука с большой длиной волны необходимы большие диффузоры. Диаметр динамика, показанного ниже, составляет 380 мм. Колонки, предназначенные для низкие частоты называются вуферами.Они имеют большую массу и поэтому трудно быстро разогнаться для высокочастотных звуков. На фотографии ниже часть вырезана, чтобы показать внутренние компоненты.

Твитеры — громкоговорители, предназначенные для высоких частот — может быть просто динамики аналогичной конструкции, но с небольшими диффузорами и катушками малой массы. В качестве альтернативы они могут использовать пьезоэлектрические кристаллы для перемещения конуса.

Динамики представляют собой линейные двигатели со скромным диапазоном — возможно, десятки мм. Подобные линейные двигатели, хотя, конечно, без бумажного конуса, часто используется для радиального перемещения считывающей и записывающей головки на дисководе.

Предупреждение: настоящие двигатели сложнее

Эскизы двигателей были схемами, чтобы показать принципы. Пожалуйста, не сердитесь, если, когда вы разбираете мотор, он выглядит больше. сложный! (Смотри как настоящие электродвигатели работают.) Например, типичный двигатель постоянного тока вероятно, будет иметь много отдельно намотанных катушек для обеспечения более плавного крутящего момента: всегда есть одна катушка, для которой синусоидальный член близок к единице. Это показано ниже для двигателя с обмотанными статорами (вверху) и постоянные статоры (внизу).

Трансформаторы

На фотографии изображен трансформатор, предназначенный для демонстрационных целей: первичная и вторичная обмотки четко разделены и могут быть удалены и заменен поднятием верхней части сердечника.Для наших целей отметим что у катушки слева меньше катушек, чем у правой (вставки показать крупные планы).

На эскизе и схеме показан повышающий трансформатор. Чтобы сделать понижающий трансформатор, достаточно разместить источник справа, а нагрузку — слева. ( Важно Примечание по безопасности : для настоящего трансформатора вы можете только «подключить его задом наперед» только после проверки соответствия номинального напряжения.) Итак, как же трансформатор работает?

Сердечник (заштрихован) имеет высокую магнитную проницаемость, т.е. материал, образующий магнитное поле намного легче, чем свободное пространство, из-за ориентации атомных диполей. (На фотографии сердечник — ламинированное мягкое железо.) В результате поле сконцентрировано внутри ядра, и почти силовые линии не выходят из ядра. Если следует, что магнитные потоки φ через первичный и вторичный примерно равны, как показано.Из Фарадея По закону ЭДС на каждом витке первичной или вторичной обмотки составляет −dφ / dt. Если пренебречь сопротивлением и другими потерями в трансформаторе, вывод напряжение равно ЭДС. Для N _p витков первичной обмотки, это дает

Для N _s витков вторичной обмотки это дает Разделение этих уравнений дает уравнение преобразователя где r — коэффициент поворотов.А что с током? Если пренебречь потерями в трансформатор (см. ниже раздел об эффективности), и если мы предположим, что напряжение и ток имеют одинаковое фазовое соотношение в первичной обмотке и вторичный, то из сохранения энергии мы можем записать в установившемся состоянии:

V _p I _p = V _s I _s, откуда

I _s / I _p = N _p / N _s = 1 / r.

Так что ничего не получишь даром: если увеличишь напряжение, то уменьшишься. ток (по крайней мере) в тот же фактор. Обратите внимание, что на фотографии катушка с большим количеством витков имеет более тонкий провод, потому что она предназначена для меньшего ток, чем тот, с меньшим количеством витков.

В некоторых случаях целью упражнения является уменьшение силы тока. В силе линии передачи, например, потери мощности при нагревании проводов из-за их ненулевое сопротивление пропорционально квадрату тока.Таким образом, передача электроэнергии от электростанции позволяет сэкономить много энергии. в город при очень высоких напряжениях, так что токи невелики.

Наконец, и снова предполагая, что трансформатор идеален, давайте спросим, что резистор во вторичной цепи «похож» на первичную цепь. В первичном контуре:

_с

V _p / I _p = V _s / r ² I _s = Р / р ².

R / r ² называется отраженным сопротивлением . При условии, что частота не слишком высока, и при наличии сопротивления нагрузки (условия обычно встречается в практических трансформаторах), индуктивное сопротивление первичной обмотки намного меньше, чем это отраженное сопротивление, поэтому первичная цепь ведет себя как если бы источник управлял резистором номиналом R / r ².

КПД трансформаторов

На практике реальные трансформаторы имеют КПД менее 100%.

Во-первых, это резистивные потери в катушках (потеря мощности I ² .r). Для данного материала сопротивление катушек можно уменьшить, сделав их поперечное сечение большое. Удельное сопротивление также можно сделать низким, используя медь высокой чистоты. (См. Дрейф скорости и закон Ома.)
Во-вторых, в сердечнике наблюдаются потери на вихревые токи.Это может быть уменьшается за счет ламинирования сердечника. Ламинирование уменьшает площадь цепей в ядре, и таким образом уменьшите ЭДС Фарадея, и, таким образом, текущий текущий в ядре, и таким образом теряется энергия.
В-третьих, в сердечнике есть гистерезисные потери. Намагничивание и кривые размагничивания магнитных материалов часто немного отличаются (гистерезис или зависимость от истории), и это означает, что требуемая энергия намагничивать сердечник (при увеличении тока) не совсем восстанавливается при размагничивании.Разница в энергии теряется в виде тепла. в основном.
Наконец, геометрический дизайн, а также материал сердечника могут быть оптимизированным, чтобы гарантировать, что магнитный поток в каждой катушке вторичной обмотки почти такой же, как и в каждой катушке первичной обмотки.

Подробнее о трансформаторах: генераторы переменного и постоянного тока

Трансформаторы работают только от переменного тока, что является одним из больших преимуществ переменного тока.Трансформеры позволяют понижать 240 В до уровня, удобного для цифровой электроники (всего несколько вольт) или для других приложений с низким энергопотреблением (обычно 12 В). Трансформеры повышайте напряжение для передачи, как упомянуто выше, и понижайте для безопасности распределение. Без трансформаторов потери электроэнергии при распределении сети, и без того высокие, были бы огромными. Возможно преобразование напряжения в DC, но сложнее, чем в AC. Кроме того, такие преобразования часто неэффективно и / или дорого.Дополнительным преимуществом переменного тока является то, что его можно использовать на двигателях переменного тока, которые обычно предпочтительнее двигателей постоянного тока для приложений большой мощности.

Другие ресурсы от нас

Некоторые внешние ссылки на веб-ресурсы по двигателям и генераторам

Гиперфизика: Электромоторы с сайта HyperPhysics в штате Джорджия. Отлично сайт габаритный, и моторный отсек для этого идеально подходит. Хорошо использование веб-графики.Имеет двигатели постоянного, переменного и асинхронного ссылки
Громкоговорители .. Еще больше хороших материалов от Государственной Гиперфизики Джорджии. Хорошая графика, хорошие объяснения и ссылки. Этот громкоговоритель сайт также включает в себя вложения.
http://members.tripod.com/simplemotor/rsmotor.htm A сайт, описывающий двигатель, построенный студентами. Ссылки на другие двигатели, построенные тот же студент и ссылки также на сайты о моторах.
http://www.specamotor.com A сайт, который сортирует двигатели различных производителей в соответствии со спецификациями, введенными пользователем.

В чем разница между постоянными магнитами и наличие электромагнитов в двигателе постоянного тока? Это делает его более эффективным или более могущественный? Или просто дешевле?

Когда я получил этот вопрос на Высшем Доска объявлений школьной физики, я отправил ее Джону Стори, который не только выдающийся астроном, но и строитель электромобилей.Вот его ответ:

В общем, для маленького мотора намного дешевле использовать постоянные магниты. Материалы для постоянных магнитов продолжают совершенствоваться и стали настолько недорогими что даже правительство время от времени присылает вам бессмысленные магниты на холодильник через почту. Постоянные магниты также более эффективны, потому что нет энергии тратится на создание магнитного поля. Так зачем вообще использовать раневое поле Двигатель постоянного тока? Вот несколько причин:

Если вы строите действительно большой двигатель, вам понадобится очень большой магнит и в какой-то момент раневое поле может подешеветь, особенно если очень Для создания большого крутящего момента необходимо сильное магнитное поле.Имейте это в виду если вы проектируете поезд. По этой причине в большинстве автомобилей есть стартеры. которые используют поле раны (хотя некоторые современные автомобили теперь используют постоянные магнитные двигатели).
У постоянного магнита магнитное поле имеет фиксированное значение (т.е. что означает «постоянный»!) Напомним, что крутящий момент, создаваемый двигателем заданная геометрия равна произведению тока через якорь и напряженность магнитного поля.С двигателем с возбужденным полем у вас есть возможность изменения тока через поле и, следовательно, изменения моторные характеристики. Это открывает ряд интересных возможностей; вы ставите обмотку возбуждения последовательно с якорем, параллельно, или кормить из отдельно контролируемого источника? Пока есть достаточно крутящий момент для преодоления нагрузки на двигатель, внутреннего трения и т. д., чем слабее магнитное поле, тем * быстрее * двигатель будет вращаться (при фиксированной Напряжение).Сначала это может показаться странным, но это правда! Итак, если вы хотите двигатель, который может производить большой крутящий момент в состоянии покоя, но при этом сильно вращаться скорости при низкой нагрузке (как продвигается конструкция поезда?), возможно раневое поле — вот ответ.
Схем
Навигация по записям
Previous post: Разборка и сборка оборудования: Основы разборки оборудования
Next post: Блокировка межосевого дифференциала: для чего нужна и как работает
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт
Поиск
Найти:
Рубрики
2019 © ИП Гатауллин Айрат Наилевич
Карта сайта

Катушка индуктивности. Обозначение на схеме и примеры её использования в электронике.

Обозначение, параметры и разновидности катушек индуктивности

Катушка индуктивности. Параметры. Виды. Обозначение на схемах

Индуктивность

Общие свойства катушек индуктивности

Основные параметры катушек индуктивности

1. Индуктивность.

2. Добротность.

3. Собственная емкость.

4. Стабильность.

Катушки индуктивности с магнитопроводами

Экранированные катушки индуктивности

Обозначение катушек с отводами и начала обмотки

4. Катушки, дроссели, трансформаторы — Условные графические обозначения на электрических схемах — Компоненты — Инструкции

Катушка индуктивности на схеме — Весёлый Карандашик

Электрический дроссель.

Графическое изображение индуктивных элементов на схеме.

Типы катушек индуктивности

Дроссель

Индуктивность. Виды катушек и контур. Работа и особенности

Индуктивность

Катушки можно разделить на типы:

Индуктивности, образующияся на частоте резонанса вычисляется по формуле:

Похожие темы:

Катушка индуктивности. Устройство и принцип работы.

Устройство и принцип работы катушки индуктивности.

Катушка индуктивности в цепи постоянного тока.

Катушка индуктивности в цепи переменного тока.

Закон индукции Фарадея: Закон Ленца

Цели обучения

Закон Фарадея и Ленца

Применение электромагнитной индукции

Сводка раздела

Концептуальные вопросы

Задачи и упражнения

Глоссарий

Избранные решения проблем и упражнения

Закон Ленца — Университетская физика, том 2

Цели обучения

Сводка

Концептуальные вопросы

Проблемы

Глоссарий

Общая физика II

— стержневой магнит, пропущенный через катушку

20.2 Электромагнитная индукция | Texas Gateway

Индуцированная электродвижущая сила

Виртуальная физика

Электромагнитная лаборатория Фарадея

Watch Physics

Индуцированный ток в проводе

Рабочий пример

ЭДС, индуцированная в проводящей катушке движущимся магнитом

СТРАТЕГИЯ

Рабочий пример

Магнитная индукция из-за изменения размера цепи

СТРАТЕГИЯ

20.3 Электромагнитная индукция — физика

Изменение магнитных полей

Виртуальная физика

Закон Фарадея

Проверка захвата

Индуцированная электродвижущая сила

Виртуальная физика

Электромагнитная лаборатория Фарадея

Контроль захвата

Watch Physics

Индуцированный ток в проводе

Контроль захвата

Рабочий пример

ЭДС, индуцированная в проводящей катушке движущимся магнитом

Стратегия

Рабочий пример

Магнитная индукция из-за изменения размера цепи

Стратегия

Электродвигатели и генераторы

Двигатели постоянного тока

Двигатели и генераторы

Генератор

Задняя ЭДС